Cardinals and Ordinals
Cardinal and ordinal numbers are related number types that are of interest in several branches of mathematics, including set theory. We will begin with cardinal numbers (or just cardinals). We can consider cardinals to be the set of natural numbers that includes zero {0, 1, 2, 3, 4, 5 ...}. Cardinals are used to indicate the size of a set, i.e. the number of members that the set contains. Another way of putting this is to say that the number of members that a particular set contains is the cardinality of that set. The number of playing cards in a standard deck of cards, for example (ignoring any Jokers) is fifty-two (52). If we consider the deck of cards to be a set, and the playing cards to be members of that set, then the cardinality of the set is fifty-two. Before we go any further it would probably be a good idea to mention that for the purposes of this discussion we are only interested in finite sets. Mathematicians who study set theory are also interested in the properties of infinite sets, but the mathematical concepts involved will not be examined here.
The cardinality of some finite set, then, is a natural number. The inclusion of zero is required in order to give the cardinality of the empty set (usually labelled ∅). The concept of cardinality was introduced by the German mathematician Georg Ferdinand Ludwig Philipp Cantor (1845 - 1918) and emerged largely as a result of his work in the field of set theory. Indeed, Cantor is considered to be the father of modern set theory. The cardinality of a set is purely dependent on the number of members the set has, regardless of the nature of the objects in the set or the order in which they appear. Two sets containing different objects can therefore have exactly the same cardinality, as long as they contain the same number of elements. The elements themselves could be anything. Examples could include numbers, letters of the alphabet, people, countries, or chess pieces. Whatever kind of set we are dealing with, we can find its cardinality simply by counting how many elements it contains.
Obviously, the ease with which we can find the cardinality of a set (i.e. count the elements) depends to some extent on how big the set is, and whether or not the number of members it contains is likely to change over time. The cardinality of a complete set of chess pieces is easy to ascertain and will not change, whereas the cardinality of the set of all English-speaking people in the world can realistically only be estimated, and will vary greatly over time. In set theory, the cardinality of a set is sometimes referred to as the power of the set. The modern notation used to denote the cardinality of a set requires vertical bars to be placed on either side of the label used to represent the set (or the representation of the set itself). Sets are frequently labelled using capital letters. So, if we have the set A = {1, 2, 3}, we can express the cardinality of A as follows:
|A| = |{1, 2, 3}| = 3
Because the cardinality of a set is not dependent upon the type of object contained by the set, or the order in which the elements are listed, we can compare the cardinality of two (or more) sets of any kind. If two sets have the same cardinality, i.e. they both contain the same number of elements, we say that there is a bijection between them. The term bijection simply means that for each object in one set, there exists an object in the second set that occupies the same position within the set. Another way of putting this is to say that each element in one set can be paired with (or mapped to) exactly one element in the other set. Consider two sets, A = {1, 2, 3} and B = {x, y, z}. If we count the number of elements in each set, we can see that both sets have a cardinality of three (3). The relationship is illustrated by the diagram below.
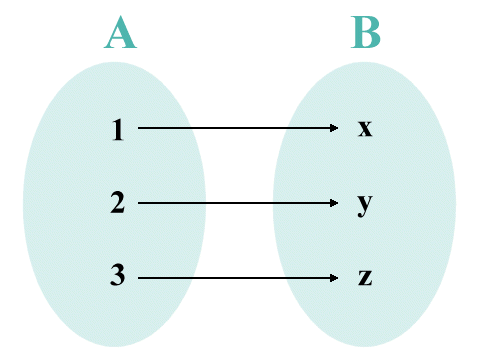
There is a bijection between sets A and B
Obviously, a mapping between two totally unrelated sets that happen to have the same cardinality is not particularly useful. Sometimes, however, there is a meaningful relationship between two sets of equal cardinality. Consider for example the International Standard Book Number (ISBN). The system uses a unique thirteen-digit number to identify books. Each edition of every book published has a different ISBN. This means that, for every edition of every book published there is one, and only one, ISBN. Similarly, each ISBN can refer to one edition, and only one edition, of a single book. There are numerous examples of such relationships. The parts list for a manufactured item will associate a single part number or code with a specific component. A social security database will pair each social security number with a particular individual. You can probably think of more examples. In set theory, the terms equipotent, equipollent and equinumerous are all sometimes used to describe the fact that two or more sets have the same cardinality. If sets A and B have the same cardinality, this can be expressed formally as follows:
|A| = |B|
While a cardinal number tells us how many elements a set contains, it gives no clue as to the ordering of the items in the set. Sometimes, of course, the ordering is of no particular importance. At other times, however, the order does matter. We can indicate the position of a particular element within a set using something called an ordinal number. We use ordinal numbers (or just ordinals) every day, in one way or another, to denote order. Consider, for example, the following statement:
Runner number four, Ethiopian runner Ayele Abshero, finished in third place in this year's London Marathon. In all, a total of thirty-four thousand, six hundred and thirty-one runners took part in the race.
There is one cardinal number in the above statement, namely thirty-four thousand, six hundred and thirty-one (34,631), which tells us the number of runners that are officially recorded as having participated in the 2013 London Marathon. The number four (4) is also mentioned, but cannot in this context be considered to be either a cardinal number or an ordinal number, since it is not related to the number of entrants, and is not explicitly associated with any particular ordering. In this context, it can be considered to be a nominal number (essentially, just a label) that identifies the runner. In the same way, the number on a footballer's shirt identifies the player, rather than the position in which they play. The ordinal number here is actually three (3), because we are told that the runner named in the article finished in third place. In other words, he was the third runner to cross the finishing line.
An ordinal number, when used in this way, tells us everything about something's position in a sequence, but nothing about the length of the sequence (i.e. its cardinality). Those of us with a modicum of historical knowledge might surmise, for example, that the term Richard the Second must refer to the second king of England to be called Richard. From that, we can infer that there must have been at least two English kings called Richard, but the term does not indicate how many kings of England called Richard there have been in total. In fact, there have been three, the last of whom was the notorious Richard the Third. When we express the position of an element in a sequence using natural language, either verbally or in writing, we use the terms first, second, third, fourth, and so on. Each of these terms is associated with one of the natural numbers, as illustrated by the examples below.
First (1st)
Second (2nd)
Third (3rd)
Fourth (4th)
Like cardinals, ordinals are of special interest to mathematicians studying set theory. Indeed, the concept of ordinal numbers emerged from Georg Cantor's work on set theory together with the concept of cardinal numbers. And, like cardinals, ordinals are also natural numbers. In set theory, ordinals have meaning only in relation to sets that are well-ordered. By definition, a well-ordered set is totally ordered (this essentially means that, for any two elements, there will always be one that is bigger than the other), and every non-empty subset of a well-ordered set has a least element. To demonstrate what this last bit means, we can say that the set of natural numbers, {0, 1, 2, 3, 4, 5 ...}, is a well-ordered set, because any non-empty subset will contain a least element. This does not hold true for the set of integers, {... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 ...}. If we take the set of negative integers as a subset of the set of integers, then clearly this subset has no least element, since there is no lower bound to the set of negative integers. To further clarify, here are some more examples:
{2, 3, 4, 5}
{6}
{9, 7, 4, 3}
First of all, we should point out that each of the sets shown here is a subset of the natural numbers, and therefore has a least element. This of course means that any non-empty subset of one of these sets will also be a subset of the natural numbers. You will intuitively look at the first set, {2, 3, 4, 5}, and consider it to be well-ordered. The remaining two sets probably need a little more explanation. The second set, {6}, has only one element (6), so the only possible non-empty subset is {6}, which is obviously the same as the original set. Note that set theorists differentiate between the broad definition of a subset, which allows the subset to contain all of the elements from the original set, and a stricter definition that does not allow this. For the purposes of defining a well-ordered set, the broad definition of a subset may be used. In the third set, {9, 7, 4, 3}, the elements are not listed in order of magnitude. This simply illustrates one of the features of set theory, which is that the order in which elements are displayed within a set is not important. A proper subset of this set might be {7, 3}, which would have the least element three (3).
In set theory, ordinals can be used in two ways. They can be used to index the elements of a well-ordered set, and they can be used to denote the order type of a well-ordered set. When used to index a set element, the ordinal acts as a label that describes the position of the element within the set. The indexing starts at zero (0), a concept that computer programmers will be familiar with. The least element is thus labelled zero (0), the next smallest element is labelled one (1), the smallest element after that is labelled two (2), and so on. The size of the set (i.e. the number of elements that the set contains) is given by the smallest ordinal that is not a label for one of the elements of the set. We call this ordinal the order type of the set. Consider the following well-ordered set:
{0, 1, 2, ..., 9, A, B, C, D, E, F}
The set contains the complete range of hexadecimal digits from zero (0) to fifteen (F). The ellipsis (...) is used as a kind of shorthand to indicate the inclusion of all of the hexadecimal digits between two (2) and nine (9), even though they are not actually shown. The following table shows the relationship between the elements of the set and the ordinals used to label them.
| Ordinal | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
We said earlier that the order type (i.e. the length or size) of the set is given by the smallest ordinal that is not a label for an element in the set. In this case, the smallest natural number that is not a label for a set element is sixteen (16). The order type of the well-ordered set {0, 1, 2, ..., 9, A, B, C, D, E, F} is therefore sixteen. Two well-ordered sets with the same order type are said to be order isomorphic. This simply means that we can create a one-to-one mapping between each element of the first set and its corresponding element in the second set. Hence, if one element in the first set is larger than another element in the first set, then the element in the second set that is mapped to the larger element will be larger than the element in the second set that is mapped to the smaller element (this is actually pretty obvious when you think about it).
A common definition of ordinals states that each ordinal is the order type of the set of all ordinals less than it. The ordinal thirty-two (32), for example, is the order type of the set {0, 1, 2, ..., 31}. From this definition, we can infer that all natural numbers are ordinals, and that every natural number can therefore be seen as the order type of the set of all natural numbers smaller than it. For all non-empty, well-ordered sets there will be a minimum element labelled with the ordinal zero (0). For finite sets, there will also be a maximum element. In the set of hexadecimal digits, {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, ..., F}, the maximum element is F, which is labelled with the ordinal fifteen (15). Obviously, if a set contains only one element, the minimum and maximum elements will be one and the same. For the empty set (∅), the order type will by definition be zero (0), since there are no ordinals less than zero.
Those studying set theory at a higher level will realise that there is much more to be said on the subject of cardinals and ordinals. The purpose of this page is simply to provide an introduction to some of the basic concepts, which we hope we have achieved.
