Factorising Quadratic Equations
Overview
The fact that many quadratic equations have two solutions has the potential to be confusing. Bear in mind, however, that we are normally looking for just one solution to a particular problem. Choosing the correct solution from two possible answers is usually a matter of recognising which of the answers is appropriate to the problem. In many cases, a negative answer would make no sense, so we can ignore such an outcome. It is very rare that we are left wondering which of the two answers (should there in fact be two answers) is the correct one. It should be clear from the above that what we are looking for is a value (or values) for x that satisfy the function y = ƒ(x) = ax 2 + bx + c = 0.
We can often factorise the left-hand side of the equation to give us two terms for x. Factorising is essentially the reverse process of multiplying out brackets to simplify an expression such as (x + 3)(x - 2), which would give us x 2 + 3x - 2x - 6 ⇒ x 2 + x - 6. Why do we want to do this? Because it leaves us with an equation like (x + 3)(x - 2) = 0. In order for such an equation to be true, one or both of the expressions inside the brackets must evaluate to zero. Therefore, either x plus three equals zero (x + 3 = 0), or x minus two equals zero (x - 2 = 0). The obvious conclusion is that x is equal to minus three or x is equal to two (x = -3 or x = 2). And that's it. We have solved the quadratic equation. Unfortunately, not all quadratic equations factorise, but many do.
The skill involved in using factorisation to solve quadratic equations comes with practice and experience, since you first of all need to be able to determine whether or not the equation will factorise in the first place, and then (assuming it will factorise) you need to find two numbers which would, if the brackets were to be multiplied out again, result in the same quadratic equation we started with. Sometimes the right numbers are easy to find, sometimes they can be somewhat elusive. You can of course check whatever answers you come up with by multiplying the brackets out again to see if you get the original quadratic equation. We can see how this works using an example. Consider the following quadratic equation:
x 2 - 4x - 5 = 0
The value of the constant term (the last constant in the equation) is minus five (-5). When the brackets are multiplied out, the constant term will be the product of the integer terms within each bracket. Because five is a prime number, it only has two factors (itself and one). Because its value is minus five, the factors could be minus five and one, or five and minus one (-5 and 1, or 5 and -1). Note that the linear coefficient (that's the number in font of x in the middle of the quadratic equation) is minus four. The integer values we are looking for (both of which will be multiplied by x when the brackets are multiplied out) must therefore sum to minus four, so we have to use minus five and one. Let's write the equation out in its factorised form:
(x - 5)(x + 1) = 0
If we now multiply out the brackets again, we get:
x 2 + x - 5x - 5 = 0
Now gather like terms together:
x 2 - 4x - 5 = 0
It works! So, we have a solution, namely that x must equal five or minus one (x = 5 or x = -1). You can see the graph for this function below (you might even recognise it, since it was used as one of the examples on the page "Quadratic Equations" in this section). If you take a look at this graph, you will see that it does indeed intersect the x-axis at x = 5 and x = -1.
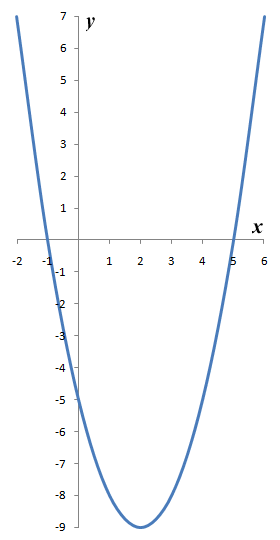
The graph of y = ƒ(x) = x 2 - 4x - 5
The method that has emerged here for factorising this type of quadratic equation is relatively straightforward. We are looking for two integer values that (a) multiply together to give the constant term and (b) add together to give the linear coefficient. Let's try another example:
x 2 - 7x + 12 = 0
The constant term here is twelve. The factors of twelve are one, two, three, four, six and twelve. We are looking for two factors with a product of twelve, but we can discount one and twelve because they do not sum to minus seven (the linear coefficient) in any combination of positive or negative values. Neither do two and six, which leaves only three and four. In order to sum to minus seven, both numbers must be negative, so we have minus three and minus four. Writing the equation out in its factorised form, we have:
(x - 3)(x - 4) = 0
Note that because we are multiplying the brackets together, the order in which they are written does not particularly matter. If we now multiply out the brackets again, we get:
x 2 - 4x - 3x + 12 = 0
Now gather like terms together:
x 2 - 7x + 12 = 0
Once again we have found two values for x. The graph of the corresponding quadratic function is shown below. The illustration below is a screenshot of the extremely useful "Quadratic Function Explorer" facility at the Math Open Reference website (http://www.mathopenref.com/quadraticexplorer.html). This time, our solution gives us x equals three or x equals four (x = 3 or x = 4). As you get more practice at factoring quadratic equations like the ones above, you will find that you can pick out the numbers you need relatively quickly and painlessly, but (you knew there was a "but" coming, didn't you!) bear in mind that the equations we have looked at so far both had a quadratic coefficient of one.
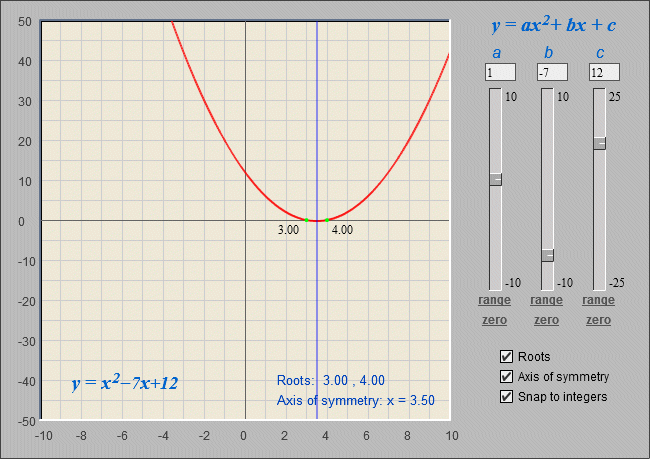
The quadratic equation x 2 - 7x + 12 = 0 has roots of x = 3 and x = 4
When the quadratic coefficient is greater than one
When the quadratic coefficient is greater than one, life becomes a tiny bit more complicated. Consider the following quadratic equation:
3x 2 + 5x - 2 = 0
We are still looking for two numbers that add together to give the linear coefficient (which in this case is five). Now, however, instead of looking for factors of minus two (the constant term), we need to find two numbers that, when multiplied together, result in the product of the quadratic coefficient and the constant term. This means we are looking for factors of minus six, i.e. three multiplied by minus two (3 × -2 = -6). The only factors of minus six that actually produce minus six when multiplied together and can be added together to produce five, are six and minus one (6 × -1 = -6, 6 + -1 = 5). This allows us to split the term 5x, and rewrite the equation as follows:
3x 2 + 6x - x - 2 = 0
We can now factorise the first two terms (3x 2 and 6x) by finding the highest common factor, which in this case is 3x:
3x (x + 2)
The highest common factor for the last two terms (-x and -2) will be -1, which gives us:
-1(x + 2)
So we now have the expressions 3x × (x + 2) and -1 × (x + 2) on the left hand side of the equation. Since the term (x + 2) is common to both expressions, we can rewrite the equation as:
(3x - 1)(x + 2) = 0
Just to be sure we have factorised correctly, we will multiply out the brackets again:
3x 2 + 6x - x - 2 = 0
Gather like terms together:
3x 2 + 5x - 2 = 0
So, since this is the same as our original equation, our factorisation is correct. This means that we have candidate values for x of one third or minus two (x = 1/3 or x = -2). Let's look at another example:
4x 2 - 6x - 4 = 0
We are looking for two numbers that add together to give the linear coefficient (minus six) and that multiply together to give the product of the quadratic coefficient (four) and the constant term (minus four), which will be minus sixteen (4 × -4 = -16). Looking at factors of minus sixteen, the obvious choices are minus eight and two, since minus eight plus two equals minus six (-8 + 2 = -6). We can now rewrite our quadratic equation to split the term 6x as follows:
4x 2 - 8x + 2x - 4 = 0
Now we factorise the first two terms (4x 2 and -8x) by finding the highest common factor, which in this case is 4x:
4x (x - 2)
The highest common factor for the last two terms (2x and -4) will be two (2), which gives us:
2 (x - 2)
So we now have the expressions 4x × (x - 2) and 2 × (x - 2) on the left hand side of the equation. Since the term (x - 2) is common to both expressions, we can rewrite the equation as:
(4x + 2)(x - 2) = 0
Again, to make sure we have factorised correctly, we will multiply out the brackets again:
4x 2 - 8x + 2x - 4 = 0
Gathering like terms together we get:
4x 2 - 6x - 4 = 0
This is the same as our original equation, so our factorisation is correct. This time we have candidate values for x of one half or two (x = 1/2 or x = 2).
The difference of two squares
Sometimes you will encounter a quadratic equation in which the linear coefficient is zero (or the term bx is omitted altogether, which amounts to the same thing), and the constant term is itself a perfect square. The following equations fit this scenario, and are equivalent to one another:
x 2 - 9 = 0
x 2 + 0x - 9 = 0
Because we are subtracting a number that is a square from another term that is also a square, we call this situation the difference of two squares or sometimes the difference of perfect squares. In the example above, we have nine (which is three squared) being subtracted from x squared (x 2). In order to factorise such an expression, we are looking for two numbers that sum to zero (because the linear coefficient is zero), and which multiply together to give the constant term. In the example above those numbers would be three and minus three. We can use these numbers to split the 0x term into two separate terms as follows:
x 2 + 3x - 3x - 9 = 0
If we factorise the first two terms we get:
x(x + 3)
Factorising the last two terms gives:
-3(x + 3)
So we now have the expressions x × (x + 3) and -3 × (x + 3) on the left hand side of the equation. Since the term (x + 3) is common to both expressions, we can rewrite the equation as:
(x - 3)(x + 3) = 0
To make sure we have factorised correctly, we will multiply out the brackets again:
x 2 + 3x - 3x - 9 = 0
Gathering like terms together we get:
x 2 - 9 = 0 (or x 2 + 0x - 9 = 0)
This is the same as our original equation, so our factorisation is correct. We have candidate values for x of three or minus three (x = 3 or x = -3). In quadratic equations of this type:
x 2 - a 2 = 0
The equation will always factorise to (x - a)(x + a). Note that you might also come across an expression such as the following:
2x 2 - 18 = 0
The two terms here have a common factor of two, so we can factorise as follows:
2(x 2 - 9) = 0
The term inside the brackets should look familiar because we have already seen it (see above). The equation therefore factors as:
2(x - 3)(x + 3) = 0
Since two is obviously not equal to zero, we still have a situation where either (x - 3) or (x + 3) must equal zero, so x is either three or minus three (x = 3 or x = -3). An alternative approach of course would be to simply divide both sides of the equation by two in the first place to get x 2 - 9 = 0. Another variation on this theme occurs when the quadratic coefficient is itself a perfect square, as in the following equation:
9x 2 - 16 = 0
Because nine is also a perfect square (9 = 3 2), the term 9x 2 can be written as (3x) 2, so we still have the difference of two squares on the left-hand side of the equation ((3x) 2 - 4 2). We can therefore factorise the equation as follows:
9x 2 - 16 = 0 ⇒ (3x - 4)(3x + 4)
Perfect squares
Sometimes the factorisation of a quadratic equation results in a single term multiplied by itself, i.e. squared. Consider the following equation:
x 2 - 8x + 16 = 0
We are looking for two numbers that multiply together to give sixteen, and add together to give minus eight. The numbers in this case both turn out to be minus four, because minus four multiplied by itself equals sixteen, and minus four plus minus four equals minus eight (-4 × -4 = 16 and -4 + (-4) = -8). We can therefore rewrite the equation, splitting the -8x term, as follows:
x 2 - 4x - 4x + 16 = 0
Factorising the first two terms we get:
x (x - 4)
And factoring the last two terms we get:
-4 (x - 4)
We now have the terms x × (x - 4) and -4 × (x - 4) on the left hand side of the equation, and we can rewrite the equation as:
(x - 4)(x - 4) = 0 ⇒ (x - 4) 2 = 0
If we multiply out the brackets again as a double-check we get:
(x - 4) 2 = 0 ⇒ (x - 4)(x - 4) = 0 ⇒ x 2 - 8x + 16 = 0
When the constant term is missing
One more case to consider when factorising quadratic equations is the situation where there is no constant term. In a case like this, you should look for factors common to the quadratic and linear terms in the equation. An example should demonstrate the principle. Consider the following quadratic equation:
3x 2 - 6x = 0
Each of the terms 3x 2 and -6x has a common factor of 3x. The common factor is then written outside the brackets, and the terms that appear inside the brackets are chosen so that multiplying out the brackets again will produce the original equation. in this example, the terms within the bracket will be x and minus two (x and -2):
3x(x - 2) = 0
This means that either 3x is equal to zero, or x - 2 is equal to zero, so x is either zero or two.
