The Quadratic Formula
The quadratic formula is used to solve quadratic equations. The formula is derived primarily from the process called completing the square (the following dialogue is based on the assumption that you are already familiar with quadratic equations and the process known as completing the square - if not, you should read the relevant pages first). The formula can find the solution to a quadratic equation expressed in the generalised form:
ax 2 + bx + c = 0
where:
- x is the variable whose value we seek
- a is a constant called the quadratic coefficient
- b is a constant called the linear coefficient
- c is a constant called the constant term
The graph of a typical quadratic function y = ƒ(x) = ax 2 + bx + c is shown below. The value of y is zero at the x-intercepts (the points at which the graph intersects the x-axis). These values of x are known as the roots of the quadratic equation ax 2 + bx + c = 0. They are the solutions we are looking for, and are the values of x that satisfy the equation.
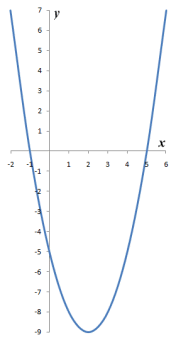
The graph of a typical quadratic function
Elsewhere in these pages we have looked at different ways of finding a solution for a quadratic equation. One of the methods used was called factorising. This is usually a relatively straightforward process, but does not work for all quadratic equations. Another method is called completing the square, which works for all quadratic equations (even those with complex coefficients, although the subject of complex numbers will be dealt with elsewhere). Depending on the terms of the equation, completing the square can sometimes involve a fair amount of work. The quadratic formula we are about to examine is largely derived from the process of completing the square, and is presented here as an alternative approach to solving a quadratic equation. The method chosen to solve quadratic equations is often a matter of personal choice. Each method has its advantages and disadvantages, and each may be better suited to solving a particular type of problem.
We will start by looking at the process of completing the square in general terms, and then examine how this technique forms the basis for the quadratic formula. Consider the general form of the quadratic equation for a moment:
ax 2 + bx + c = 0
We can isolate the constant term (c) by rewriting the equation as follows:
ax 2 + bx = -c
Let's also assume for the moment that we are dealing with a monomial form of the quadratic equation. That is a quadratic equation in which the quadratic coefficient (a) is one. We can represent the terms on the left-hand side of the equation (x 2 + bx) graphically as follows:
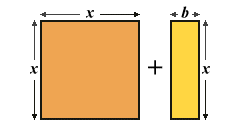
A graphical representation of x 2 + bx
If you recall the algebraic method used for completing the square, we essentially took half the value of the linear coefficient (b), called it a (just to confuse you!), and then rewrote the left hand side of the equation as (x + a) 2. This gives us a perfect square on the left-hand side of the equation, but multiplying out the brackets gives us x 2 + 2ax + a 2. How does this affect the graphical representation shown above? First of all, you need to remember that the variable we call a here is totally unrelated to the variable we call a in the general form of the quadratic equation. More importantly, the value of a is exactly half that of the linear coefficient (b). If we represent the terms x 2, 2ax and a 2 graphically, this is what we get:
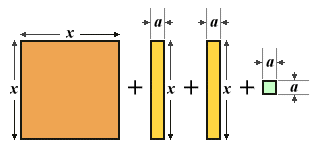
A graphical representation of x 2 + 2ax + a 2
We still have the original squared term (x 2) as well as the rectangle representing bx, although now split into two equal halves. We also have an additional squared term (a 2) which we did not have before. This term has to be added to the right-hand side of the equation as well in order to balance things up. But why have we done this? Remember that the object of the exercise in the first place was to complete the square, i.e. to get a term on the left hand side of the equation that was a perfect square. We can see that the expression (x + a) 2 on the left-hand side of the equation is indeed a perfect square, but presenting this graphically might helps us to visualise what is going on. So, let's rearrange our pictorial representation somewhat:
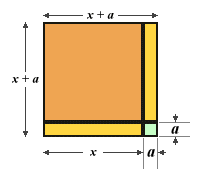
A graphical representation of (x + a) 2
As you can see from the illustration, the square representing x 2 plus the two rectangles representing 2ax (or the two halves of the rectangle that originally represented bx) almost form a square. The square must be completed, however, by adding the missing corner, which is the square representing a 2. The quadratic formula is written with reference to the terms used in the general form of the quadratic equation, so we could rewrite our completed square as:
| ( | x + | b | ) | 2 |
| 2 |
If we multiply out the brackets and simplify, we get:
| x 2 + bx + | ( | b | ) | 2 |
| 2 |
Remember that earlier we re-wrote the generalised quadratic equation to isolate the constant term (c) on the right-hand side of the equation as follows:
ax 2 + bx = -c
We are going to replace the left-hand side of the equation with the complete square. The difference between the original left-hand side of the equation and the complete square is the term (b/2) 2, so we must add this term to the right-hand side to balance things up:
| ( | x + | b | ) | 2 = | ( | b | ) | 2 - c ⇒ | ( | x + | b | ) | 2 = | b 2 | - c |
| 2 | 2 | 2 | 4 |
We can now take the root of both sides:
| x + | b | = √ | ( | b 2 | - c | ) |
| 2 | 4 |
Finally, we re-arrange the equation to isolate x on the left-hand side:
| x = | b | ± √ | ( | b 2 | - c | ) |
| 2 | 4 |
The problem here is that this only works when the quadratic equation is a monomial equation with a quadratic coefficient of one (a = 1). Assuming that a could have values other than one, we need to factor a out of our quadratic term (ax 2) by dividing both sides of the quadratic equation by a:
| x 2 + | b | x + | c | = 0 |
| a | a |
Now we move the constant term to the right-hand side:
| x 2 + | b | x = - | c |
| a | a |
Now, to complete the square, we add (b/2a) 2 to both sides:
| x 2 + | b | x + | ( | b | ) | 2 = | ( | b | ) | 2 - | c | ||
| a | 2a | 2a | a |
Where did we get the term (b/2a) 2 ? You recall from earlier that the perfect square for the left-hand side of the monomial version of the quadratic equation was the expression (x + b/2) 2. Since we have divided all of the terms in the equation by a, this will now become (x + b/2a) 2. We are going to expand the term (b/2a) 2 on the right-hand side of the equation, which leaves us with the following:
| ( | x + | b | ) | 2 = | b 2 | - | c |
| 2a | 4a 2 | a |
We now have two rational values on the right-hand side of the equation. To give us a common denominator for both terms, we can multiply the numerator and denominator of the term -c/a by 4a to give us:
| ( | x + | b | ) | 2 = | b 2 | - | 4ac | ⇒ | ( | x + | b | ) | 2 = | b 2 - 4ac |
| 2a | 4a 2 | 4a 2 | 2a | 4a 2 |
Taking the root of both sides:
| x + | b | = | √ | b 2 - 4ac |
| 2a | 4a 2 |
Isolating x:
| x = - | b | ± | √ | b 2 - 4ac | ⇒ x = - | b | ± | √ | (b 2 - 4ac) | |
| 2a | 4a 2 | 2a | 2a |
Simplifying this equation gives us:
| x = | -b ± √(b 2 - 4ac) |
| 2a |
This is the quadratic formula as it is normally written. The term underneath the radic (the root symbol) is called the discriminant of the quadratic formula. This term (b 2 - 4ac) will determine what kind of solution we can expect to find. A quadratic equation with real coefficients may have either one or two real roots, or two complex roots. The discriminant tells us the number and nature of the roots. If the discriminant evaluates to a positive value, there are two distinct real roots. If the discriminant evaluates to zero, there is a single real root (sometimes called a double root). If the discriminant evaluates to a negative value, there are no real roots (but there will be two distinct complex roots). Let's try solving the following quadratic equation:
2x 2 - 4x - 3 = 0
Because the quadratic coefficient is not one, if we want to factorise this equation we need two numbers that add together to give the linear coefficient (which in this case is four), and that multiply together to give the product of the quadratic coefficient and the constant term. We are therefore looking for factors of minus six, (two multiplied by minus three) but there are no factors of minus six that can be added together to produce four. This means we need to use an alternative method of solving the equation, so we will apply the quadratic formula:
| x = | -(-4) ± √((-4) 2 - 4(2)(-3)) |
| 2(2) |
| x = | 4 ± √(16 + 24) |
| 4 |
| x = | 4 ± √40 |
| 4 |
| x = | 4 ± √4√10 |
| 4 |
| x = | 4 ± 2√10 |
| 4 |
| x = | 2 ± √10 |
| 2 |
| x = | 2 + √10 | or x = | 2 - √10 |
| 2 | 2 |
| x ≈ 2.5811388 or x ≈ -0.5811388 |
Note that the determinant evaluates to a positive number (forty), so the equation has two real roots. The graph of the function y = ƒ(x) = 2x 2 - 4x - 3 is shown below, and confirms our result.
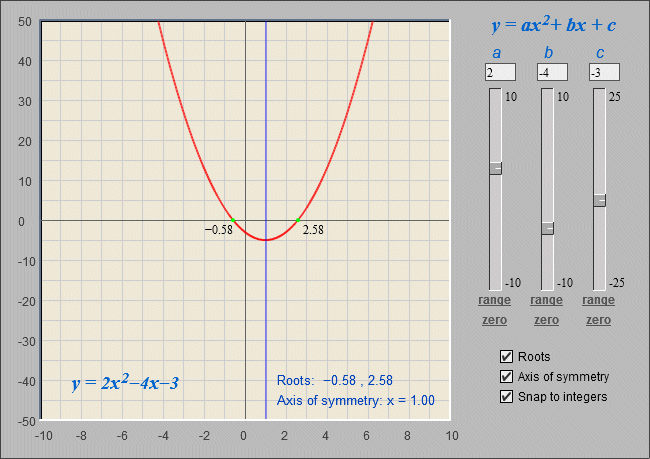
The quadratic equation 2x 2 - 4x - 3 = 0 has roots of x = 2.58 and x = -0.58
Here is another example:
2x 2 + 4x + 2 = 0
This equation can be factorised, so although we will apply the quadratic equation to it we will carry out the factorisation for the sake of comparison. We need two numbers that add together to give the linear coefficient (which in this case is four), and that multiply together to give the product of the quadratic coefficient (two) and the constant term (also two). We are therefore looking for factors of four, so the obvious choice for both numbers is two (two multiplied by two is four, two plus two is four). We can thus split the term 4x, and rewrite the equation as follows:
2x 2 + 2x + 2x + 2 = 0
We factorise the first two terms (2x 2 and 2x) by finding the highest common factor, which in this case is 2x:
2x(x + 1)
The highest common factor for the last two terms (2x and 2) will be 2, which gives us:
2(x + 1)
We now have the expressions 2x (x + 1) and 2 (x + 1) on the left hand side of the equation. Since the term (x + 1) is common to both expressions, we can rewrite the equation as:
(2x + 2)(x + 1) = 0
In fact, there is only one solution for this equation:
2x + 2 = 0 ⇒ 2x = -2 ⇒ x = -1
x + 1 = 0 ⇒ x = -1
Applying the quadratic formula, we get:
| x = | -4 ± √(4 2 - 4(2)(2)) |
| 2(2) |
| x = | -4 ± √(16 - 16) |
| 4 |
| x = | -4 ± √0 |
| 4 |
| x = | -4 |
| 4 |
| x = -1 |
Because the discriminant evaluates to zero in this example, there is only one solution and we can expect to see a graph that touches the x-axis at a single point. Here is the graph of the function y = ƒ(x) = 9x 2 + 12x + 4, which confirms our result:

The quadratic equation 2x 2 + 4x + 2 = 0 has a double root (x = -1.0 and x = -1.0)
We will now look at an example that has no solution:
3x 2 + 4x + 2 = 0
Since this equation will not factorise, we have to try other means of finding a solution. With the quadratic formula, we get the following:
| x = | -4 ± √(4 2 - 4(3)(2)) |
| 2(3) |
| x = | -4 ± √(16 - 24) |
| 6 |
| x = | -4 ± √-8 |
| 6 |
Once we can see that the term under the radic is negative, we can immediately say that there are no real roots for this quadratic equation (when we start looking at complex numbers, it will become apparent that we can find a solution to the problem, which involves complex roots). Here is the graph for the corresponding quadratic function, which confirms that there is no x-intercept, and hence no real roots for the quadratic equation:
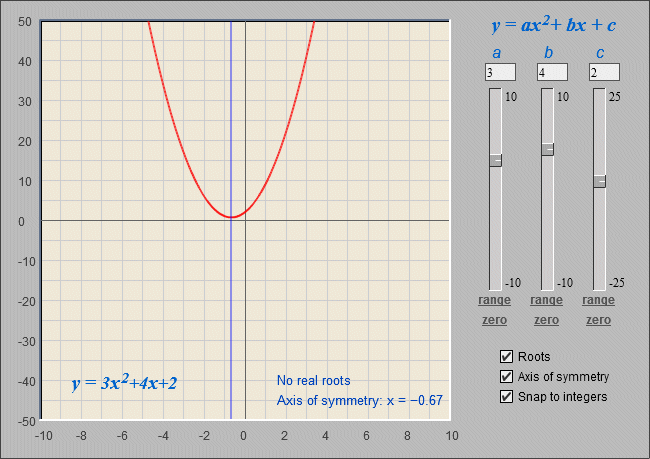
The quadratic equation 3x 2 + 4x + 2 = 0 has no real solution
