Mean Value Theorem
The mean value theorem is a generalisation of Rolle's theorem, which is the subject of another page in this section. Like Rolle's theorem, it can be applied to any non-constant function that is continuous over a defined closed interval and differentiable over the corresponding open interval. We have talked about intervals previously, but it might be a good idea at this point to briefly explain the difference between the terms closed interval and open interval. A closed interval between two points on the x axis, a and b, is denoted by enclosing the labels used for the points within square brackets and separating them with a comma, thus: [a, b]. An open interval between the same two points is denoted in exactly the same way, except that parentheses are used instead of square brackets, thus: (a, b). The difference is that while a closed interval includes its end points, an open interval does not.
An early form of the mean value theorem is thought to have been known to the Indian mathematician and astronomer Vatasseri Parameshvara Nambudiri (circa 1380-1460), who developed his mean value type formula for the inverse interpolation of the sine - which essentially means he developed a technique for calculating the sine of a given angle - based on the principles we now associate with the mean value theorem. The modern version of the mean value theorem was stated by the French mathematician Baron Augustin-Louis Cauchy (1789-1857). In fact, as you will no doubt discover for yourself if you take further studies in the field of mathematics, there are at least two versions of the mean value theorem in circulation. The other major version is Lagrange's mean value theorem, which is named after the Italian mathematician and astronomer Joseph-Louis Lagrange (1736-1813).
For the purposes of this discussion, we will simply refer to this theorem as the mean value theorem, and concentrate on the basic principles. As mentioned above, the mean value theorem is essentially a generalisation of Rolle's theorem. Like Rolle's theorem, it makes a statement about a non-constant function that is continuous over a defined closed interval and differentiable over the corresponding open interval. Unlike Rolle's theorem, the values taken by the function at each end of the interval do not have to be the same. Suppose we have a function ƒ(x) that is continuous on some interval [a, b]. The function will take the value ƒ(a) at one end of the interval, and ƒ(b) at the other end of the interval. The mean value theorem tells us that there must be at least one point c between a and b on the x axis at which the tangent to point ƒ(c) is parallel to the secant connecting the points ƒ(a) and ƒ(b). The principle is illustrated below.
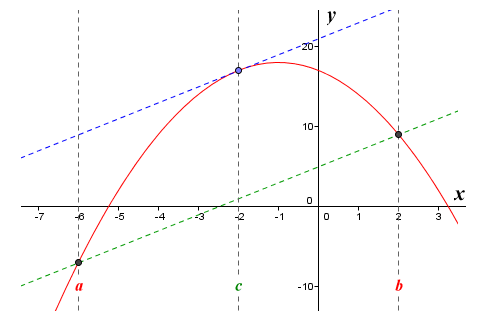
The graph of the function ƒ(x) = -x 2 - 2x + 17
The illustration shows the graph of the function ƒ(x) = -x 2 - 2x + 17 defined on the interval [a, b], where a is equal to minus six (-6), and b is equal to two (2). The value of the function at a will be:
ƒ(a) = -a 2 - 2a + 17 = -36 + 12 + 17 = -7
and the value of the function at b will be:
ƒ(b) = -b 2 - 2b + 17 = -4 - 4 + 17 = 9
Let's think about what the theorem is telling us. It's saying that the slope of the secant joining points ƒ(a) and ƒ(b) is the same as the slope of the tangent at point ƒ(c). That should be fairly easy to check. First, we will use the equation of a straight line to find the slope m of the secant:
| m = | y2 - y1 | = | ƒ(b) - ƒ(a) |
| x2 - x1 | b - a |
| m = | -7 - 9 | = | -16 | = 2 |
| -6 - 2 | -8 |
Remember that the slope of the tangent at point ƒ(c) will be the derivative of the function applied to the value c. The derivative of the function ƒ(x) = -x 2 - 2x + 17 is obtained by simply applying the basic rules of differentiation:
| d | (-x 2 - 2x + 17) = -2x - 2 |
| dx |
Applying the derivative to ƒ(c) we get:
| d | (ƒ(c)) = -2c - 2 |
| dx |
Looking at the graph, we can see that the value of c in this case is minus two (-2) so we get:
| d | (ƒ(c)) = -2(-2) - 2 = 2 |
| dx |
So, we can see that the slope of the tangent at point ƒ(c) is indeed the same as the slope of the secant connecting points ƒ(a) and ƒ(b).
We can now define the mean value theorem a little more formally by saying that, if a function ƒ(x) is continuous on the closed interval [a, b] and differentiable on the corresponding open interval (a, b), then there must exist a value c within the open interval (a, b) such that a < c < b and:
| d | (ƒ(c)) = | ƒ(b) - ƒ(a) |
| dx | b - a |
Or alternatively, using Lagrange notation:
| ƒ′(c) = | ƒ(b) - ƒ(a) |
| b - a |
Now let's think about why the theorem is called the mean value theorem. For a function that is continuous on the closed interval [a, b] and differentiable on the corresponding open interval (a, b), the slope of the secant connecting the interval end points ƒ(a) and ƒ(b) represents the average rate of change of the function's value. At some point within that interval there will be a point ƒ(c) such that a < c < b and the tangent to point ƒ(c) will be parallel to (i.e. have the same slope as) the secant connecting ƒ(a) and ƒ(b). Remember that the slope of the tangent is also the derivative at point ƒ(c), and therefore represents the instantaneous rate of change at that point.
The mean value theorem is therefore essentially telling us that, for a function that is both continuous on a closed interval and differentiable on the corresponding open interval, there will be at least one point within the open interval for which the function has an instantaneous rate of change that matches its average rate of change. There are numerous real-world situations to which this principle can be applied. The speed at which a vehicle moves, for example, is a measure of the rate at which its position changes as a function of time. It follows that, in a given interval of time, a moving vehicle will have both an average speed and an instantaneous speed. The mean value theorem tells us that, for any time interval during which the vehicle is moving, the instantaneous speed of the vehicle will match the average speed at least once.
Think of a car travelling along a motorway for one hour at an average speed of seventy miles per hour. There are only two ways in which this could be achieved. One way is if the car travels at a constant speed of seventy miles per hour for the entire hour. This is unlikely, but theoretically possible. The other (more realistic) scenario is one in which the car travels at speeds of less than seventy miles per hour for some of the time, and speeds in excess of seventy miles per hour for some of the time. Notice that we did not say "and speeds in excess of seventy miles per hour for the rest of the time." That is because there must be at least one instant in time when the car is travelling at exactly seventy miles per hour. In other words, there are moments in time when the car's instantaneous speed matches its average speed.
Like the intermediate value theorem and Rolle's theorem (of which it is a generalisation), the mean value theorem doesn't give us any concrete results in terms of numbers. It simply tells us that, for a continuous and differentiable function defined on some interval, the function's instantaneous rate of change will match its average rate of change for at least one point within that interval. It doesn't tell us where within the interval this will occur, or how often. Nevertheless, the mean value theorem is one of the most important theorems in calculus. It has numerous applications, ranging from solving relatively trivial problems like finding the number of roots that exist for a polynomial equation, to helping to prove the fundamental theorem of calculus itself (that's the theorem that defines the relationship between the two most important concepts in calculus – differentiation and integration).
