Angles
Overview
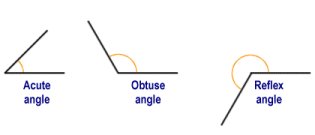
An angle (from the Latin angulus, meaning corner) is created whenever two line segments or rays meet at a common end point. Wherever this occurs, two angles are formed. Normally, one of the angles will be an acute angle, a right angle or an obtuse angle. The other angle will be a reflex angle (the meaning of these terms is illustrated below). The rays or line segments form the sides of each angle, while the point at which the sides meet forms the vertex of each angle. In some cases, two rays or line segments may converge on a common point from opposite directions. If this is the case, both of the angles created will be straight angles. If the two rays or line segments are both pointing in the same direction, a single angle is formed which is a complete rotation (a second angle is sometimes said to exist, called the zero angle). Here are the different kinds of angle you will encounter:
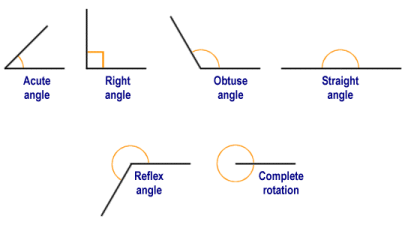
Different types of angles created at the junction of two rays or line segments
The size of the angles created by two rays or line segments is dependent on the degree to which one of the lines would need to be rotated around the point of convergence, either clockwise or anti-clockwise, in order for both of the lines to be pointing in the same direction. The main unit of measurement used to describe the size of an angle is the degree (or degree of arc). The degree symbol is a small raised circle ("°") which appears immediately following a number to denote that the number represents the size of an angle in degrees (note that the same symbol is used to represent temperature values expressed as degrees, but the context in which appears is usually sufficient to prevent confusion between the two). One degree represents a rotation of one three hundred and sixtieth (1/360) of a full circular rotation.
If an angle must be written with more precision than the use of degrees alone can provide, its value can be expressed using some number of decimal places (e.g. 48.75°). Alternatively, the degree is sometimes sub-divided into sixty equal units called arc minutes (or just minutes). Each of these units can itself be divided into sixty sub-divisions called arc seconds (or just seconds). This degree of precision is only really used in disciplines such as astronomy, or for specifying the latitude and longitude of a geographical location on earth, where very small differences can be significant. For the purposes of these pages, we will either express angles to the nearest degree or use decimal notation.
The different types of angle can be defined as follows:
- Acute - greater than zero degrees and less than ninety degrees ( > 0° and < 90° ).
- Right angle - exactly ninety degrees (90°). The rays or line segments are said to be perpendicular to one another.
- Obtuse angle - greater than ninety degrees, and less than one hundred and eighty degrees ( > 90° and < 180° ).
- Straight angle - exactly one hundred and eighty degrees (180°). Two line segments effectively become a single, longer line segment. Two rays effectively become a line.
- Reflex angle - greater than one hundred and eighty degrees and less than three hundred and sixty degrees ( > 180° and < 360° ).
- Complete rotation - exactly three hundred and sixty degrees (360°). The two rays or line segments have the same point of origin and point in the same direction.
Measuring angles in radians
A radian is the angle subtended by an arc of a circle (i.e. part of the circumference of a circle) whose length is equivalent to the radius of the circle. In other words, it is the acute angle created by the junction of two rays that originate from the centre of the circle and pass through opposite end points of the arc. The principle is illustrated below.
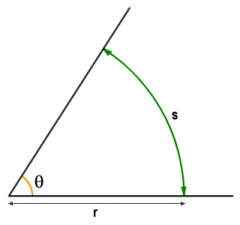
Angle θ is the angle subtended by arc s, and is one radian when the length of s equals that of r
For any arc s of a circle of radius r, the angle θ subtended by the arc (in radians) will be the quotient of s and r (i.e. the length of the arc divided by the radius of the circle). The circumference of a circle is given as 2πr where π (sometimes written as pi) is a constant with an approximate value of three point one four (3.14). Given that a circle represents one complete rotation of three-hundred and sixty degrees (360°), one radian represents an angle of just over fifty-seven degrees (57°), as the following calculation shows:
| 360 | ≈ | 360 | ≈ 57.3° |
| 2π | 6.28 |
The sign of an angle
We have seen that an angle is formed at the junction of two rays or line segments, which form the sides of the angle. The sign of the angle (i.e. whether it is considered to be positive or negative in value) depends on which of the two sides we measure the angle from. The side we choose for this purpose is called the initial side. The other side of the angle is called the terminal side. Angles are said to be positive if we measure the degree of rotation between the initial side and the terminal side in an anti-clockwise direction. If we measure the degree of rotation between the initial side and the terminal side in a clockwise direction, then the angle is said to be negative. Incidentally, if we wish to measure the angle of an oblique line, ray or line segment (i.e. any line, ray or line segment that is neither horizontal nor vertical) and an initial side is not specified, then the initial side is assumed to be the x-axis in the Cartesian plane.
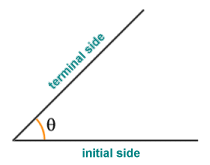
An angle is measured from the initial side to the terminal side
In the illustration above, θ denotes a positive angle of forty-five degrees (45°) and represents an anti-clockwise rotation between the initial side and the terminal side. The reflex angle (measured as a clockwise rotation between the initial side and the terminal side) would be a negative angle with a value of minus three hundred and fifteen degrees (-315°). Note that the concept of negative angles is not used in a navigational context. Compass bearings, for example, are always measured from north in the clockwise direction. A heading of north-west would therefore give a bearing of three hundred and fifteen degrees (315°).
Identifying angles
As we have seen above, angles are often labelled using a letter from the Greek alphabet. The lower case Greek letter theta ("θ") is frequently used to identify an angle for which the value is initially unknown. Lower case characters from the Latin alphabet (e.g. a, b, c etc.) are also commonly used to identify angles. In the case of a geometric figure such as a triangle, the points that define the figure are often labelled using upper case Latin characters (e.g. A, B, C etc.). In the illustration below, the figure shown is a pentagon represented by points A, B, C, D and E. Since angle θ has sides defined by the line segments AB and AC, it may also be referred to using the notation ∠BAE or ∠EAB (note the use of the angle symbol, "∠"). The order in which the characters appear is not particularly important, so long as the character that identifies the vertex of the angle is in the middle.
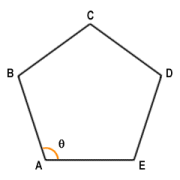
Angle θ may also be referred to as ∠BAE or ∠EAB
When labelling the vertices of a figure like the one illustrated, the convention is to label them clockwise, and in alphabetical order. If angles are identified using the labels of the three vertices that define them, a similar convention is normally adopted. The angle θ would therefore be identified as ∠EAB. Of course, the sign of the angle is not immediately obvious using this notation. Nor is it clear whether the angle referred to is the acute angle defined by the points E, A and B, or the reflex angle defined by the same points. The context will usually make it clear which angle is being referred to, and will allow the initial and terminal sides to be identified if necessary in order for the sign of the angle to be determined. Unless otherwise stated, it is usually assumed that the angle referred to is the smaller of the two angles (i.e. less than one hundred and eighty degrees), and that the sign of the angle is positive.
Some properties of angles
- The sum of the angles created by some number of rays or line segments that radiate out from a single point is three hundred and sixty degrees (360°).
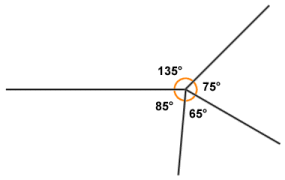
Angles around a single point sum to 360 degrees
- The sum of the angles created on one side of a straight line by the line itself and some number of rays or line segments radiating out from a single point on the line is one hundred and eighty degrees (180°).
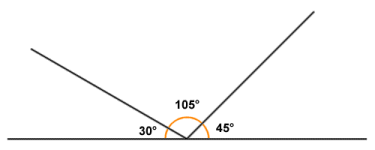
Angles around a single point on one side of a line sum to 180 degrees
- Any angle that is not a right-angle or some multiple thereof (i.e. ninety degrees, one hundred and eighty degrees, two-hundred and seventy degrees or three-hundred and sixty degrees) is said to be an oblique angle.
All of the above types of angles are oblique angles
- Angles of the same magnitude (i.e. where the degree of rotation between the initial side and the terminal side is identical) are said to be congruent. The length of each side of the angles, and the direction in which they are pointing, are unimportant so long as the degree of rotation between the sides in each angle is the same.
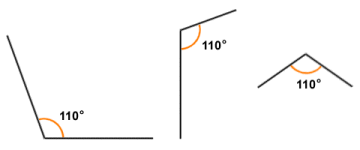
The three angles shown here are congruent
- When two lines intersect each other, two pairs of angles are formed as shown below. A pair of angles formed by the intersection of two lines and lying on opposite sides of the intersection are called vertical angles or opposite angles (or vertically opposite angles) and are always equal in magnitude.
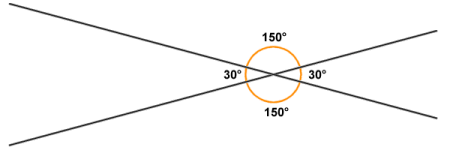
At the intersection of two lines, opposite angles are always equal
- Two angles that have a common side and do not overlap, and whose vertex occurs at the same point, are said to be adjacent angles.
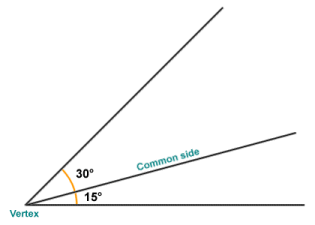
The angles shown here are adjacent
- Two angles that, when added together form a right angle (ninety degrees), are called complementary angles. The difference in size between any given angle and a right angle is called the complement of that angle.
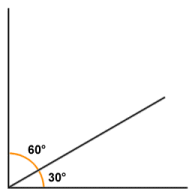
Two angles that sum to 90 degrees are said to be complementary
- Two angles that, when added together form a straight angle (one hundred and eighty degrees), are called supplementary angles. The difference between any given angle and a straight angle is called the supplement of that angle. Note that the non-common sides of two adjacent angles that sum to one hundred and eighty degrees (180°) will lie on the same line. Two angles that are adjacent and supplementary are referred to as a linear pair.
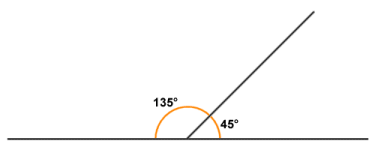
Two angles that sum to 180 degrees are said to be supplementary
- Two angles that sum to three hundred and sixty degrees (360°) are called explementary angles or conjugate angles.
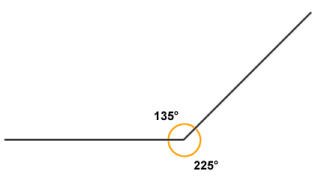
Two angles that sum to 360 degrees are said to be explementary
- A line that crosses two parallel lines (see below) is called a transversal. Two lines are said to be parallel if they lie in the same plane (i.e. they are coplanar) and never intersect one another. In total, eight (8) angles are created at the intersections between two parallel lines and a transversal. The four angles that lie between the parallel lines are known as interior angles, while those that lie outside the parallel lines are called exterior angles. Note that all angles marked a are equal, and all angles marked b are equal.
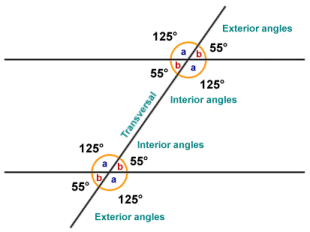
A line that crosses two parallel lines is called a transversal
- As shown in the illustration below, alternate interior angles (i.e. interior angles that lie on opposite sides of the transversal) are equal in magnitude, i.e. they are congruent. Interior angles that lie on the same side of the transversal always sum to one hundred and eighty degrees (180°), and are thus supplementary.
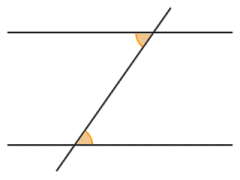
Alternate interior angles are congruent
- As shown below, alternate exterior angles (exterior angles that lie on opposite sides of the transversal) are equal in magnitude (congruent). Exterior angles that lie on the same side of the transversal are supplementary.
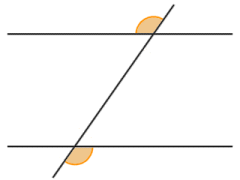
Alternate exterior angles are congruent
