Cylinders
The term cylinder can be used to describe the surface formed by all of the points that are equidistant from a line segment (the line segment may be considered to lie on the axis of the cylinder). This surface essentially forms a straight, hollow tube of finite length. Let's assume that, instead of a hollow tube, we have a solid rod with the same dimensions, bounded at each end by flat circular faces that are perpendicular to the axis. In terms of solid geometry, this object is also a cylinder. It is the solid version of the cylinder that we are interested in here. The cylinder may be considered to be a circular prism, i.e. a prism that has two circular base faces (if we ignore the strict definition of a prism, which states that its base faces must be polygons).
In most cases, when the term cylinder is used, it refers to a right circular cylinder, i.e.one for which the base faces are congruent circles that are perpendicular to the axis of the cylinder. Other types of cylinder exist. In an oblique circular cylinder for example, the base faces are still parallel congruent circles, but are offset from one another (i.e. they are not perpendicular to the axis of the cylinder). In an elliptical cylinder, the base faces are ellipses. For the most part, we are only really interested here in the right circular cylinder.
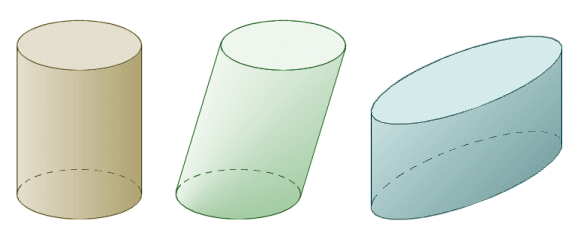
A right circular cylinder (left), oblique circular cylinder (middle) and elliptical cylinder (right)
All of these cylinder types can be considered to be prisms if we ignore the strict definition of a prism (i.e. that the base faces must be polygons). They all match the definition of a prism in other respects, since the base faces are parallel and congruent. Furthermore, the cross-section through each cylinder parallel to its base faces, at any point between the two base faces, will be the same. For that reason, the general formula for the volume V of a prism can be applied equally well to cylinders:
| V = | 1 | Bh |
| 3 |
where B is the area of the base of the cylinder and h is the vertical height (or altitude) of the cylinder (i.e. the perpendicular distance between the base faces). For circular cylinders (both right and oblique), the base faces are circles. Since the area of a circle is given as πr 2, where r is the radius of the circle, we can modify the formula for the volume of a prism to give us a better formula for the volume of a right or oblique circular cylinder as follows:
V = πr 2h
Note that the line that passes through the centre of each base face of a circular cylinder is called its axis. For a right circular cylinder, the axis will be perpendicular (i.e. at ninety degrees) to each base face, and will also be the cylinder's axis of symmetry.
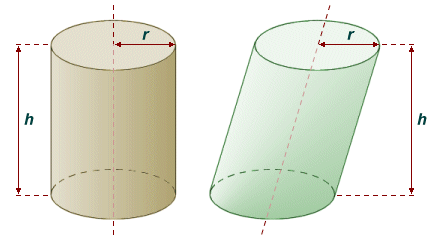
The volume of a right or oblique circular cylinder depends only on its base radius and height
Finding the surface area for a right circular cylinder is also relatively straightforward. The total surface area of the right circular cylinder can be broken down into three components. Two of those components are the two base faces of the cylinder, which we know are circles. The area of each circular base face is given by πr 2, so these two components together have a total area of 2πr 2. The third component is the lateral surface of the cylinder (i.e. the curved wall of the cylinder). This surface can be visualized as a rectangle, created by cutting the cylinder wall along a line parallel with the axis of the cylinder, and then flattening it out.
The resulting rectangle has a length corresponding to the perimeter of either of the base faces, and a height equaling the height of the cylinder. The perimeter of a circle is given as 2πr, so the lateral surface area of the cylinder will be 2πrh. We can now put the expressions for the area of the base faces and the lateral surface area together to obtain a formula for the total surface area A of a right circular cylinder:
A = 2πr 2 + 2πrh = 2πr (r + h)
Finding the surface area of an oblique circular cylinder is also relatively straightforward, but instead of the perpendicular height (i.e. the altitude) of the cylinder, we need to consider its length. The length l of the cylinder is the distance between two corresponding points on the base faces of the cylinder. In a right circular cylinder, the length will coincide with both the vertical height (altitude) of the cylinder and the length of the axis of the cylinder. In an oblique circular cylinder, however, the length of the cylinder coincides only with the length of the axis of the cylinder, as shown in the illustration below.
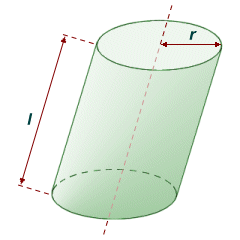
The surface area of an oblique circular cylinder depends on its base radius and length
The formula for the area of an oblique circular cylinder is thus slightly different to the formula for the area of a right circular cylinder, because we must replace the height h with the length l, as follows:
A = 2πr 2 + 2πrl = 2πr (r + l)
