The Dihedral Angle
A dihedral angle (sometimes called a torsion angle) is the angle φ (lower case Greek letter phi) formed by the intersection of two planes. The angle can be seen (at least theoretically) by looking at the planes "edge on", or in other words along the line of intersection. Obviously for two Euclidean planes, which are infinite, this would not be possible, but there are many examples in our everyday lives of finite planes intersecting. Such intersections commonly occur at right angles (think about the intersections that occur between floors, walls and ceilings in your house, in an office, or in some other building). The line of intersection may be referred to as the edge of the dihedral angle. It is generally accepted that the dihedral angle between two parallel planes is zero degrees. If the dihedral angle is a right-angle, the planes are referred to as perpendicular planes (this will normally be the case with the dihedral angle between walls, floors and ceilings, for example).
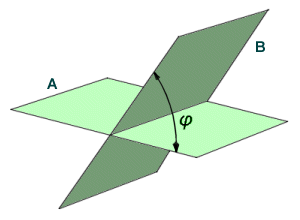
The angle between two planes is called the dihedral angle
Consider the diagram below. A dihedral angle is formed by the intersection of planes P and Q. The dihedral angle is the angle between the two planes, and will be the same as the angle between the straight line segments AB and CD, which are perpendicular to planes P and Q respectively. This is useful to know, because while vectors that lie in the plane itself may have an infinite number of directions, the direction that is perpendicular to a plane (known as the normal vector) is unique to that plane (and, of course, any plane that is parallel with it). Assuming that we have sufficient information to find the normal vector for each plane, we can calculate the dihedral angle (this will however involve using trigonometry, so we will not delve into it here).
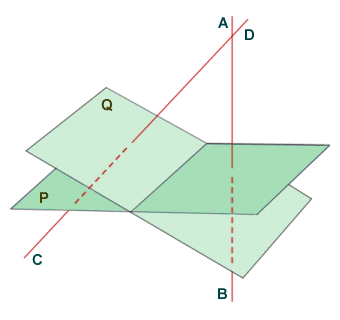
The angle between line segments AB and CD is equal in magnitude to the dihedral angle
Dihedral angles are of interest in many branches of science and engineering, as well as mathematics. We are interested in dihedral angles here from the point of view of studying polyhedra. A polyhedron is a many-sided three-dimensional shape with straight edges and flat faces. The faces of a polyhedron are effectively finite planes, and the edges along which these faces meet are the edges of the dihedral angle between the adjacent faces. The simplest example of a polyhedron is probably the cube, which has six (6) identical faces that form twelve (12) identical dihedral angles (which are all right-angles).

A cube has six identical faces and contains twelve identical dihedral angles
