Ellipses
An ellipse is the shape of a section through a cone or a right circular cylinder that does not pass through the base (in the case of a cone) or either of the base faces (in the case of a right circular cylinder). The shape produced is a smooth, closed curve. The illustration below shows a couple of examples. A circle is a special case of the ellipse that is obtained when the section through the cone or cylinder is orthogonal to the axis of the cone or cylinder (i.e. parallel to the base of the cone, or to the base faces of the cylinder). If you are unfamiliar with the characteristics of cones or right circular cylinders, you might want to have a look at the relevant pages in this section.

An ellipse is the shape that results from a section through a cone or a right circular cylinder
An ellipse is symmetrical about its horizontal and vertical axes, as you can see from the illustration below. The maximum distance between two antipodal points occurs along the horizontal axis (called the major axis or transverse diameter), and the minimum distance between two antipodal points occurs along the vertical axis (called the minor axis or conjugate diameter). Antipodal points are any two points on the perimeter of the ellipse such that the line segment joining them must pass through the centre C of the ellipse (which occurs at the intersection of the horizontal and vertical axes).
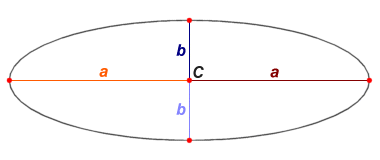
An ellipse is symmetrical about its major and minor axes
One half of an axis (i.e. that part of an axis that lies between the centre C and the perimeter of the ellipse) is known as a semi-axis. A semi-axis belonging to the major axis is called a semi-major axis, and a semi-axis belonging to the minor axis is called a semi-minor axis. In the diagram above, we have labelled each of the two semi-major axes a, and each of the two semi-minor axes b. The points shown in red on the perimeter of the ellipse are the points where the major and minor axes intersect the perimeter of the ellipse. These are the vertices and co-vertices of the ellipse. The vertices are the points at which the curvature of the ellipse is at its maximum (i.e. where the major axis intersects the perimeter of the ellipse). The co-vertices are the points at which the curvature of the ellipse is at its minimum (i.e. where the minor axis intersects the perimeter of the ellipse).
There are two special points that lie on the major axis of the ellipse, equidistant from its centre C, each of which is a focus of the ellipse. These two points (jointly referred to as the foci of the ellipse) are usually labelled F1 and F2. The location of the foci is such that, for any point P on the perimeter of the ellipse, the sum of the distances from F1 to P and from F2 to P remains constant, and will equal the length of the major axis. In fact, taking any arbitrary pair of points as the foci, and any value for the length of the major axis that is greater than the distance between these two points, then the corresponding ellipse is defined as the set of points for which the sum of the distances between a point and each of the foci is equal to the length of the major axis.
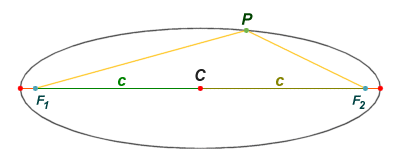
The sum of the distances between the foci and any point on the ellipse is a constant
The distance between either of the foci and the centre of the ellipse is called the focal distance, and will be a function of the lengths of the semi-major and semi-minor axes. We have labelled the line segments connecting each focus with the centre of the ellipse c. The length of c (i.e. the focal distance ) can be found using the following formula:
c = √(a2 - b2)
where a and b are the lengths of the semi-major and semi-minor axes respectively. Note that the further away the foci are from the centre of the ellipse, the smaller the resemblance between the ellipse and a circle. The curvature at the vertices of the ellipse will increase, while the curvature at the co-vertices will diminish. In other words, the ellipse will become flatter as the value of c increases.
If we move the foci closer together, the result will be that the ellipse becomes more like a circle. Indeed, if the foci are moved to the centre of the major axis, so that F1 is equal to F2 is equal to C, and c equals zero, then the ellipse will be a circle with a radius equal to a, and the major and minor axes will be the same length. The degree to which an ellipse deviates from being a circle, i.e. the more "squashed" it becomes, is called its eccentricity. The eccentricity is usually denoted by the lower case Greek letter Epsilon (ε), and is a function of the focal distance c and the length of the semi-major axis a such that:
| ε = | c |
| a |
Since the length of the semi-major axis a will always be greater than the focal length c, then the value of ε will always be between one and zero. If the focal length c is zero (i.e. the foci F1 and F2 coincide with the centre C of the ellipse), then the value of ε also becomes zero. An eccentricity of zero indicates that the ellipse is a circle. As the foci move closer to the ends of the major axis, the value of ε will tend towards one, and the ellipse will become increasingly elongated. If the foci were to coincide with the ends of the major axis, the value of ε would become one, and the "ellipse" would in fact be a line segment.
Finding the area of an ellipse is pretty straightforward. The area A of an ellipse is the product of the semi-major axis a and the semi-minor axis b, multiplied by Pi (π). We can write the formula as follows:
A = πab
The length of the perimeter (or circumference) of the ellipse is somewhat trickier to calculate. At least, it is if a high degree of accuracy is required. The formula for the length of the perimeter p of an ellipse is given as follows:
p = 4aE(ε)
where a is the length of the semi-major axis and ε is the eccentricity of the ellipse. The term E represents something called the complete elliptic integral of the second kind and yes, it is indeed quite as nasty as it sounds. Suffice it to say that in order to obtain an exact value for E, a significant amount of computation is required that involves integration (one of the major elements in the branch of mathematics known as calculus). A foray into the realms of calculus is a little beyond the scope of this page, but a reasonable approximation of the length of the perimeter of an ellipse can be obtained using the following formula:
p = π√(2 (a2 + b2))
