The Parallelepiped
Cubes, cuboids and parallelepipeds are closely related three-dimensional polyhedra (a polyhedron is any three-dimensional shape that has straight edges and flat faces). For reasons we shall explore shortly, you can probably think of the parallelepipeds as a family of shapes to which cuboids belong. Not all parallelepipeds are cuboids, but all cuboids are parallelepipeds. Similarly, cubes are a subset of the cuboid family and, although all cubes are cuboids (and hence also parallelepipeds), not all cuboids are cubes. Cubes and cuboids are discussed elsewhere. This page is primarily concerned with parallelepipeds that are not cubes or cuboids.
A parallelepiped is a convex three-dimensional shape with straight edges and flat faces (i.e. a polyhedron). The parallelepiped has six (6) faces (and is thus by definition also a hexahedron), each of which is a parallelogram. Pairs of opposite faces are congruent and parallel. The parallelepiped has twelve (12) edges, and eight (8) vertices. The edges of the parallelepiped can be grouped into three (3) sets of four (4) edges for which, within each set, the edges are parallel and of equal length. The parallelepiped is also a zonohedron. A zonohedron is a shape for which every face has point symmetry. That means that looking towards the central point of a face from two opposite directions, whatever those directions happen to be, you will always see exactly the same thing.
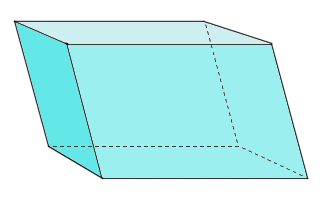
The parallelepiped has six faces, each of which is a parallelogram
As with most geometrical shapes, we are interested in features such as the total surface area and the volume of the parallelepiped. The total surface area of the parallelepiped is simply the sum of the areas of each of the six faces of the parallelepiped, each of which is a parallelogram. As with any quadrilateral, the area of a parallelogram is the product of the length of its base and height. One side of the parallelogram is taken to be the base of the parallelogram (it doesn't really matter which), and the height is then the shortest (i.e. perpendicular) distance between the side chosen to be the base and the side opposite to it. Remember also that opposite faces of the parallelepiped will be congruent, and thus have the same area.
The volume of the parallelepiped is the product of the area of the base of the parallelepiped and its height. The base of the parallelepiped can be any one of its six faces. The height of the parallelepiped is the shortest (i.e. perpendicular) distance between the face chosen to be the base of the parallelepiped and the face that is opposite to it. The principle is illustrated below.
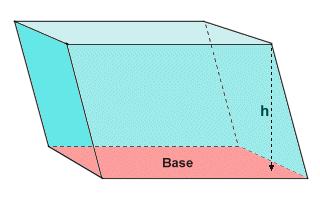
The volume of a parallelepiped is the area of its base multiplied by its height
Of course, the method used to find the volume of a parallelepiped will very much depend on the information we are given. We can for example, choose to view the three edges that meet at one of the parallelepiped's eight vertices as three-dimensional vectors. The diagram below illustrates this scenario. The vectors are labelled a, b and c. If we know the x, y and z components of each vector, the volume of the parallelepiped will be the absolute value of the scalar triple product of these three vectors. Finding the scalar triple product of three vectors is explained in the page entitled "The scalar triple product", which you can find in the Vectors and Vector Arithmetic section. In a nutshell, it involves finding the determinant of a three-by-three matrix, each row of which consists of the x, y and z components of one of the three vectors.
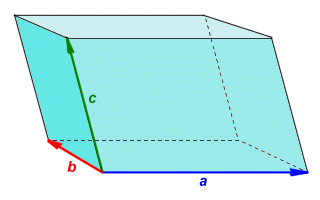
The volume of the parallelepiped will be the scalar triple product of vectors a, b and c
