Quadrilaterals
Overview
A quadrilateral (from the Latin "quadri", meaning "square" and "latus", meaning "side") is a four-sided polygon (a polygon is a flat, enclosed shape with multiple straight edges). There are several types of quadrilateral, all with their own distinct characteristics. There are certain characteristics, however, that are common to all simple quadrilaterals. There is also a type of quadrilateral called a complex or crossed quadrilateral, which we will talk about later. Unless otherwise stated, the term quadrilateral is used here to refer only to simple quadrilaterals. As well as having four sides, quadrilaterals have four vertices, four internal angles, and two diagonals (a diagonal is an imaginary line that connects opposite vertices). The sum of the internal angles is always three hundred and sixty degrees (360°). Incidentally, it is worth noting that the sum of the internal angles S for any polygon is related to the number of sides n that the polygon has by the following formula:
S = (n - 2) 180°
A simple quadrilateral has four sides and four internal angles
When talking about quadrilaterals, we often refer to the relationships between the various sides and angles. Perhaps most importantly, we distinguish between sides or angles that are consecutive, and those that are opposite one another. To avoid any possible confusion later on, here are some brief definitions, with reference to the simple quadrilateral shown above, of what these terms actually mean:
- Consecutive angles - two angles are consecutive if their vertices are connected by a common side. Angles ABC and BCD are consecutive.
- Opposite angles - two angles are opposite if they are not consecutive. Angles ABC and CDA are opposite.
- Consecutive sides - two sides are consecutive if they intersect at a common vertex. Sides CD and DA are consecutive.
- Opposite sides - two sides are opposite if they are not consecutive. Sides BC and DA are opposite.
Types of quadrilateral
Different types of quadrilaterals have different properties that are determined by the specific relationship between the sides and angles of the quadrilateral. It is perfectly possible to have a quadrilateral in which no two sides and no two angles are the same. On the other hand any two or more sides may be equal in length, and any two or more angles may be of the same magnitude. In addition, one or both pairs of opposite sides may be parallel. Many of the configurations result in shapes that have specific names, and at least some of these names are probably familiar to you. Examples of the various configurations are shown below, together with the name given to each shape and a brief description of its characteristics.
- Square - probably the easiest type of quadrilateral to work with because of its simplicity, and certainly one of the most recognisable. The square is said to be equilateral because all four sides are of equal length (this makes the square both a regular polygon and a regular quadrilateral), and all four internal angles are right-angles (i.e. ninety degrees). The diagonals in a square are of equal length, bisect each other, and are orthodiagonal (i.e. they cross at right-angles). By definition, a square is also a rectangle, a parallelogram and a rhombus (see below).
A square has four equal sides and four right-angles
- Rectangle - like the square, all four internal angles are right-angles (i.e. ninety degrees), opposite sides are of equal length, and the diagonals are also of equal length and bisect each other. Adjacent sides may however be of different lengths. By definition, a rectangle is also a parallelogram.
Only opposite sides of a rectangle are required to be equal
- Parallelogram - both pairs of opposite sides are parallel (hence the name), opposite sides are of equal length, and opposite angles are of equal magnitude. The diagonals, although only of equal length when the parallelogram is a square or a rectangle, always bisect each other. Either diagonal splits the parallelogram into two congruent triangles. Consecutive angles are supplementary (i.e. they always sum to one hundred and eighty degrees). Note that a parallelogram in which adjacent sides are of different lengths, and in which all of the internal angles are oblique, is sometimes called a Rhomboid (as opposed to a Rhombus, which is a parallelogram in which all four sides are the same length - see below).
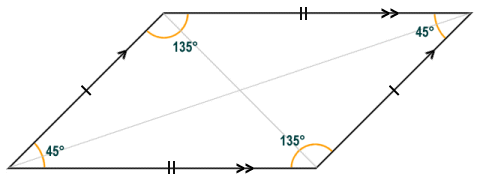
The parallelogram shown here is a rhomboid
- Rhombus - the rhombus is an equilateral parallelogram, i.e. it has four sides of equal length. Because it is a parallelogram, opposite sides are parallel, opposite angles are of equal magnitude, consecutive angles are supplementary (i.e. they sum to one hundred and eighty degrees), and the diagonals bisect each other. The diagonals of the rhombus also bisect the internal angles and are orthodiagonal (i.e. they cross at right-angles).
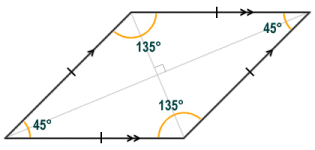
A rhombus is an equilateral parallelogram
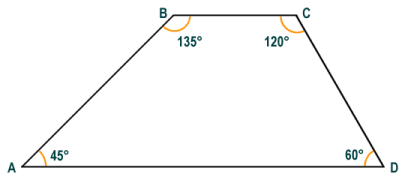
- Trapezium - this is the name used outside of North America, where it is called a trapezoid. Although opinions differ on the strict definition of a trapezium, the one we will use here is that a trapezium is a quadrilateral that has one pair, and one pair only, of opposite sides that are parallel. The illustration below shows three possible variations of the trapezium. The figure on the left is an isosceles trapezium in which the angles adjacent to each of the parallel sides are equal, and both the non-parallel sides and the diagonals are equal in length. The central figure has one side that is perpendicular to both parallel sides, so the trapezium contains two right-angles. The last (rightmost) figure has non-parallel sides of different lengths, and all of the internal angles are different.

Various configurations are possible for a trapezium
- Kite - the kite is distinguished by the fact that it has two pairs of congruent (i.e. of equal length) adjacent sides. Neither pair of opposite sides is parallel (if they were, given that adjacent sides are equal, then the resulting quadrilateral would be either a rhombus or a square). The diagonals of the kite are orthogonal (i.e. they cross at right-angles), and the longest diagonal divides the kite into two congruent triangles. Opposite angles on either side of the longest diagonal are equal in magnitude.
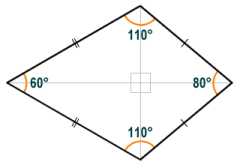
The kite has two pairs of congruent sides
- Dart - like the kite, the dart - sometimes called the arrowhead or chevron - has two pairs of congruent (i.e. of equal length) adjacent sides. None of the sides are parallel, and the diagonals of the kite are orthogonal (i.e. they cross at right-angles). Unlike the kite, the diagonals intersect outside the shape, and one of the angles (the angle adjacent both of the shorter sides) is a reflex angle (i.e. greater than 180°). Opposite angles on either side of the diagonal that bisects this reflex angle are equal in magnitude. All of the quadrilaterals up to this point have been convex (i.e. none of the internal angles have exceeded one hundred and eighty degrees). The presence of an internal angle in excess of one hundred and eighty degrees means that the dart is a concave quadrilateral. It is also possible to have a similar (concave) quadrilateral in which no two sides have the same length.
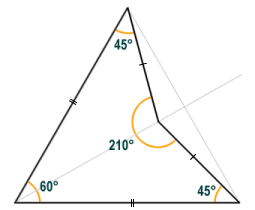
The dart is a concave quadrilateral
Inscriptible quadrilaterals
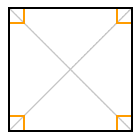
Any quadrilateral in which all four sides are tangential to an inscribed circle (i.e. a circle drawn entirely within the quadrilateral that touches all four sides) is said to be inscriptible (or tangential). Of the quadrilaterals we have looked at above, only the square, rhombus and kite are inscriptible (see illustration below). In order for a quadrilateral to be inscriptible, it must be a convex quadrilateral, and the lengths of any pair of opposite sides must sum to the same total length.
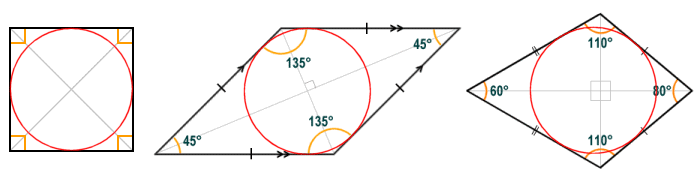
The square, rhombus and kite are all examples of inscriptible quadrilaterals
Circumscriptible quadrilaterals
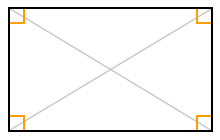
Any quadrilateral in which all four vertices lie on the same circle is said to be circumscriptible (or cyclic). Of the quadrilaterals we have looked at above, the square, rectangle, kite and isosceles trapezium are all circumscriptible (see illustration below). A quadrilateral that is both circumscriptible and inscriptible is said to be bicentric. The square is an example of a bicentric quadrilateral. A kite may also be bicentric if it has two opposite angles that are right-angles (these kites are called right kites).
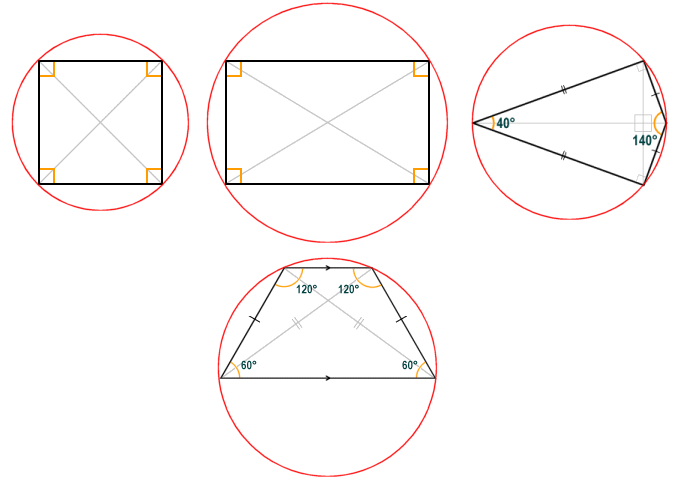
The square, rectangle, right kite and isosceles trapezium are all circumscriptible quadrilaterals
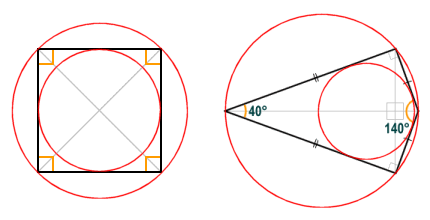
The square and the right kite are examples of bicentric quadrilaterals
Bimedians and the centroid
A bimedian is a line segment that connects the midpoints of opposite sides of a quadrilateral. The bimedians of a quadrilateral bisect one another, and in the case of a parallelogram the point at which they intersect is known as the centroid. Any line that passes through the centroid of a parallelogram will divide the parallelogram into two equal areas. If the parallelogram were to be fabricated from a flat sheet of some suitable material of uniform thickness and density, the centroid would be the centre of mass for this quadrilateral object. In the diagram below, the bimedians are labelled, and the point at which they intersect is the centroid. A third line is shown that passes through the centroid and divides the parallelogram into two equal areas.
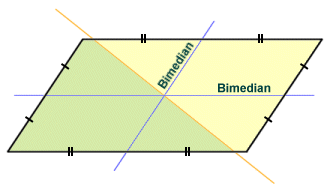
Any line through the centroid divides the parallelogram into two equal areas
Finding the area of a quadrilateral
Finding the area of a square or a rectangle is a simple matter providing you know the length of the base b and the height h of the quadrilateral, in which case the area A is given by the formula:
A = b × h
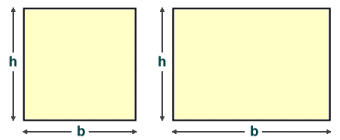
The area of a square or a rectangle is the product of the length of the base and the height
Finding the area of a parallelogram or a rhombus (which is simply an equilateral parallelogram) is also relatively straightforward. We can think of a parallelogram as a rectangle that has had a right-angled triangle removed from one end and stuck onto the other end. The principle is illustrated below. You can see from the diagram that reversing this process will result in a rectangle that has the same area as the parallelogram, since we have not actually removed anything. The base dimension will also remain the same for the rectangle as for the parallelogram, since we have simply taken part of the base from one end of the parallelogram and stuck it onto the other end. Providing you know the length of the base (b) and the height (h) of the quadrilateral, you can use the same formula to find the area of a parallelogram or a rhombus as for a square or a rectangle (area = b × h).
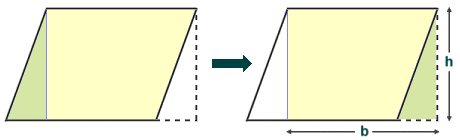
The area of a parallelogram or a rhombus is also the product of the length of the base and the height
Finding the area of a trapezium is not quite so straightforward. Just as we did with the parallelogram, however, we can break the trapezium down into simple shapes to see how the area might be calculated:
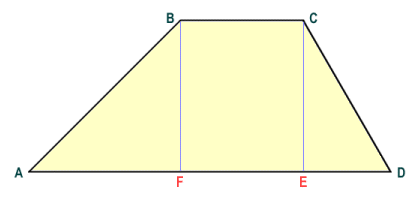
A trapezium can be broken down into simple shapes
From the diagram we can see that the total area of trapezium ABCD will be the sum of the areas of the rectangle FBCE and the right-angled triangles ABF and ECD. Now let's added the length of the shorter parallel side of the trapezium (the top of the trapezium) to the longer parallel side (the base of the trapezium) and create a rectangle like the one shown below. In addition to the rectangle FBCE and triangles ABF and ECD, our new rectangle contains exact duplicates of these shapes, and thus has an area double that of the original trapezium. To get the area of a trapezium, therefore, simply add the lengths of the two parallel sides together, multiply the answer by the height of the trapezium (this will be the perpendicular distance between the two parallel sides), and then divide the result by two.
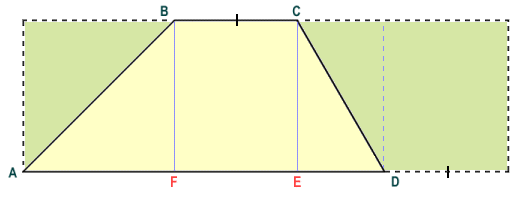
The rectangle has double the area of the original trapezium
We can perform a similar exercise with the kite. Because the diagonals of the kite are perpendicular (at right-angles) to one another, the kite can be broken down into two pairs of congruent, right-angled triangles. We can draw a rectangle EFGH around kite ABCD as illustrated below. You should be able to see from the diagram that triangles ABO, AEB, AOD and ADH are congruent. Similarly, triangles BCO, BFC, DOC and DCG are also congruent. The sum of the areas of the triangles within the kite shape and the sum of the areas of the triangles outside the kite shape must therefore be equal. It follows that the area of rectangle EFGH must be exactly double that of kite ABCD. We can see that the base GH of the rectangle is equal in length to diagonal AC, and the height EH of the rectangle is equal to the length of diagonal BD. The area of the rectangle can thus be calculated as the product of the diagonals of the kite, and the area of the kite itself will be half that of the rectangle.
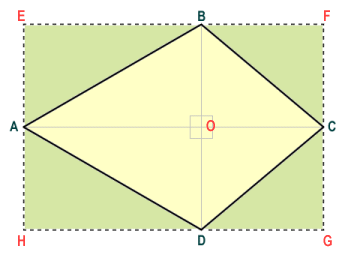
The rectangle has double the area of the kite that it contains
Finding the area of a dart presents a different challenge, because the shape is concave (as opposed to the convex shapes we have looked at above). We can apply the same principle as previously, however, and break the dart down into two congruent triangles. The area of a triangle can be calculated easily by multiplying the length of the base of the triangle by its height, and then dividing the result by two. Since triangles ABC and ACD (see illustration below) are congruent, all we have to do to find the area of dart ABCD is find the length of the base and the height of triangle ACD, and calculate their product.
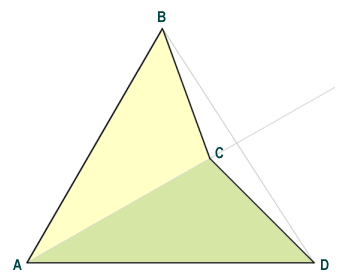
The dart can be viewed as two congruent triangles
So far, we have dealt with finding the areas of different kinds of quadrilateral shapes on a case by case basis. Not all quadrilaterals fit into one of the categories we have looked at so far however, and it would be helpful to have a general formula for finding the area of any convex quadrilateral. As you might expect, a formula that works for all cases is somewhat more involved than one that applies only to one specific type of quadrilateral. Several such formulae do exist, however. One of the best known of these is given as:
| Area = √ | ( | (s - a)(s - b)(s - c)(s - d) - | (ac + bd + pq)(ac + bd - pq) | ) |
| 4 |
where:
- a, b, c and d represent the lengths of the sides of the quadrilateral (a and c make up one pair of opposite sides, b and d make up the other)
- p and q are the diagonals of the quadrilateral
- s is the sum of the lengths of the four sides divided by two (i.e. half of the perimeter of the quadrilateral, otherwise known as the semi-perimeter):
| s = | a + b + c + d |
| 2 |
In order to test the formula, we will use irregular convex quadrilateral ABCD (shown below). The quadrilateral has no two sides or angles that are the same, but like all convex quadrilaterals it can be broken down into two triangular shapes using one of the diagonals. We will use this fact to double check the answer we get using the general formula for the area of a quadrilateral.
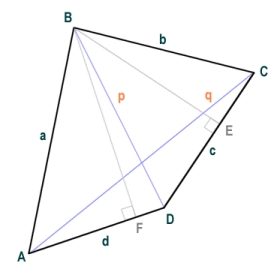
This quadrilateral has no two sides or angles the same
The length of the sides a, b, c, and d, and the lengths of the diagonals p and q have been found by measurement (the units used are not really important for this exercise) and are as follows, accurate to two decimal places:
a = 5.10
b = 4.12
c = 3.61
d = 3.16
p = 4.47
q = 6.40
The value of s is given by:
| s = | (5.10 + 4.12 + 3.61 + 3.16) | = | 15.99 | = 8.0 |
| 2 | 2 |
The value of (s - a)(s - b)(s - c)(s - d) is given by:
(2.9)(3.88)(4.39)(4.84) = 239.08
The value of (ac + bd + pq)(ac + bd - pq) is given by:
(18.41 + 13.02 + 28.61) × (18.41 + 13.02 - 28.61) = 60.04 × 2.82 = 169.31
And the area of the quadrilateral is thus:
| Area = √ | ( | 239.08 - | 169.31 | ) |
| 4 |
Area = √(239.08 - 42.33)
Area = √196.75 = 14.03
We can double check the answer using triangles ABD and BCD. Taking triangle ABD first, let the base of the triangle be side AD and the height of the triangle be line segment BF (this being the perpendicular line segment from side AD to vertex B). We already know that side AD measures 3.16 units, and line segment BF has been measured as 4.43 units (accurate to two decimal places), so we get:
| Area of triangle ABD = | AD · BF | = | 3.16 × 4.43 | = 7.0 |
| 2 | 2 |
Now taking triangle BCD, let the base of the triangle be side CD and the height of the triangle be line segment BE (this being the perpendicular line segment from side CD to vertex B). We know that side CD measures 3.61 units, and line segment BE has been measured as 3.88 units (accurate to two decimal places), so we get:
| Area of triangle ABD = | CD · BE | = | 3.61 × 3.88 | = 7.0 |
| 2 | 2 |
The area of quadrilateral ABCD is equal to the area of triangle ABD plus the area of triangle BCD, so we get:
Area of quadrilateral ABCD = 7.0 + 7.0 = 14.0
There is a very marginal difference in the two results we obtained here that can be attributed to rounding errors. A degree of impreciseness can also creep into the calculation (using either method) depending on the accuracy with which measurements are taken. You may feel from looking at the above that breaking an irregular convex quadrilateral down into two triangles to obtain the area is the easier option, and from the point of view of the complexity of the calculations involved, you would be right. On the other hand, whereas we can easily measure the sides and diagonals of a quadrilateral, finding the height of a triangle can be slightly trickier because it usually involves finding the perpendicular from whatever side you have selected as the base to the opposite vertex. This may require you to undertake some kind of construction (e.g. using a protractor or a pair of compasses) to find said perpendicular before you can actually measure it.
Complex quadrilaterals
A complex quadrilateral (often referred to as a crossed quadrilateral or a butterfly quadrilateral among other things) is one in which two non-adjacent sides intersect each other, as illustrated below. Contrary to what you might intuitively assume, there are only four vertices and four internal angles (although two of these have been effectively turned inside out). The point at which the crossover occurs between opposite sides does not constitute an additional pair of vertices. One way of visualising how a complex quadrilateral is formed is by imagining a simple convex quadrilateral (say a square or a rectangle). Imagine what would happen if you were to take one of the sides of the quadrilateral and twist it around its midpoint through one hundred and eighty degrees. Imagine for the moment that the adjacent sides are made of elastic to allow them to accommodate this rotation without becoming detached. The result would be a complex quadrilateral like those shown below.
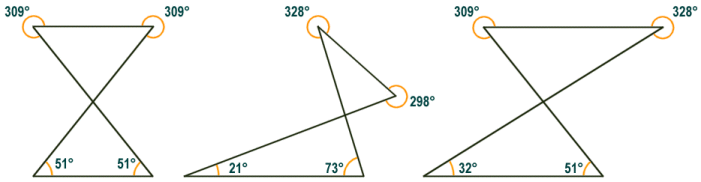
The interior angles of a complex quadrilateral sum to 720°
Note from the diagram that a complex quadrilateral may have two sides that are parallel, in which case the diagonally opposite internal angles will be explementary or conjugate (i.e. they sum to three hundred and sixty degrees). The left-most shape above has two pairs of equilateral sides, one of which are parallel. Such a shape is sometimes called an anti-parallelogram. One thing that all complex quadrilaterals have in common is that they can all be viewed as a pair of triangles that have at least one internal angle in common. Although we do not offer a general formula for finding the area of a complex quadrilateral here, the area can be calculated as the sum of the areas of the constituent triangles. These areas are calculated as the product of the length of the base and the height of each triangle. You will need to make an arbitrary choice of which side to use as the base in each case. The height is then the length of the perpendicular line segment that connects the base to the opposite vertex.
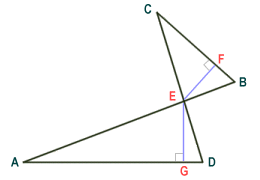
The area of a complex quadrilateral can be found using triangles
In complex quadrilateral ABCD (see above), the area of the quadrilateral can be calculated by finding the sum of the areas of triangles ADE and BCE. We have taken the base of triangle AED as side AD, and that of triangle BCE as side BC. The height of the triangles will be the length of perpendicular EG (for triangle ADE) and the length of perpendicular EF (for triangle BCE). The formula for the area of the quadrilateral can thus be written as:
| Area of quadrilateral ABCD = | AD · EG + BC · EF |
| 2 |
