The Solid Angle
Imagine a huge sphere, painted white on the inside. Next imagine a glass cube, somewhat smaller than the sphere, but floating within it in a central position. Finally imagine yourself floating at the exact centre of the sphere, looking out through the walls of the glass cube. One of the faces of the cube has been darkened so that you cannot see through it. There is therefore an area of the inner surface of the sphere that you cannot see. Think about the proportion of the inner surface of the sphere that cannot be seen. That is what we are interested in here, for reasons that will shortly be explained. If your viewpoint, the centre of the cube, and the centre of the sphere are all coincident (and provided of course that the sphere is large enough to completely contain the cube), the proportion of the inner surface of the sphere that you cannot see will remain constant, regardless of the relative sizes of the cube and the sphere.
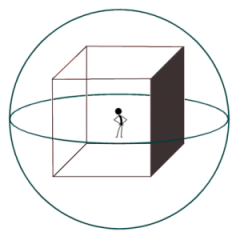
The stick man has a partially obscured view of the inside of the sphere
The area of the inner surface of the sphere that cannot be seen from the viewpoint of the stickman can be mapped out using projection. We do this by drawing a line from the centre of the sphere to each corner of the darkened face of the cube. Then we extend each of these lines until they intersect the surface of the sphere. The points at which the lines intersect the surface of the sphere form the corners of our projection. The area covered by the projection, expressed as a fraction of the total surface area of the sphere, is called the solid angle, and is represented by the upper case Greek letter Omega (Ω). The term angle is perhaps misleading, since what we are really talking about here is the total surface area of some arbitrary sphere that is obscured by an object viewed from the centre of the sphere. The object can be either two-dimensional or three-dimensional, and need not be regular in shape.
We might, for example, be projecting a circle onto a sphere. Obviously a circle does not have corners. We will probably need to draw quite a few lines from the centre of the sphere to the edges of the circle and then extend them before we can accurately map the projection of the circle onto the sphere's surface. What is important here is the proportion of the sphere's surface area obscured by the projection. It is that, and not the shape of the projection, that will determine the solid angle. Two separate projections may cover different areas on the surface of the sphere, and be completely different in shape. If the areas covered are the same size, they will represent the same solid angle.
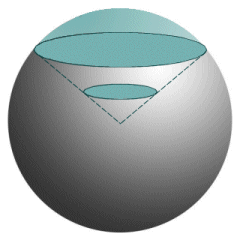
The proportion of the sphere's surface covered by the projection represents the solid angle
In the case of the solid angle formed by the projection of a disc onto the surface of the sphere, we can think of the solid angle as a cone. The cone has its apex at the centre of the sphere and extends to infinity, with the area subtended on the surface of the sphere being one of its spherical cross sections. Another way of thinking about the solid angle is to see it as a measure of how big things look to an observer. The sun and the moon, for example, look approximately the same size in the sky. The sun (which you should never look at directly, by the way) is of course considerably larger than the moon, but the moon is a lot closer to the observer.
If we think of the sky as part of an infinitely large celestial sphere that surrounds us, then the solid angle subtended by the sun or the moon represents the proportion of the total surface area of that sphere occupied by one of those objects, which is (very approximately) 0.005%. Clearly, a relatively small object nearby can subtend the same solid angle as a much larger object that is far away - one of the reasons that the moon will from time to time totally eclipse the sun. It is interesting to note, incidentally, that an observer standing at the equator over a period of several hours will be able to see the entire celestial sphere as the Earth turns. An observer standing at one of the poles, on the other hand, only sees half of the celestial sphere.
Obviously, the solid angle of any projection may be expressed as a fraction or a percentage of the total surface area of the sphere that it subtends. Our cube, for example (see above), has six identical faces and its centre is coincident with that of the sphere. The solid angle subtended by the darkened face is thus 4πr 2/6 = 2πr 2/3. From the point of view of mathematicians, the solid angle does not have a unit of measure. The International System of Units (SI) nevertheless defines a unit for the solid angle called the steradian (abbreviated to sr). One steradian is defined as an area equivalent to the square of the radius of the sphere, or r 2. Since the total surface area of a sphere is given as 4πr 2, it follows that the total surface area of the sphere in steradians is equal to 4π sr. Given any object for which we are interested in finding the solid angle, let the area of the sphere's surface covered by the object's projection be S. The solid angle Ω subtended by the object will be given by:
| Ω = | S |
| r 2 |
Conversely, if the solid angle Ω and the radius r of the sphere are both known, we can find the surface area S of the projection as follows:
S = Ω r 2
The solid angle is of interest in various branches of science and engineering. We have already seen that the solid angle subtended by a celestial body (as seen from a viewpoint on Earth) will depend on both its size and its distance from the Earth. The solid angle is therefore of great importance for astronomers. Closer to home, we are interested in things like the attenuation of signals that are transmitted from a directional antenna. The term attenuation means the amount of signal strength lost over a given distance. A signal transmitted from an Earth station to a communication satellite in space, for example, has only a fraction of its original strength when it reaches the satellite's receiver.
The predominant reason for this loss of signal strength is that the signal, which originates from a focused directional antenna on the Earth's surface with a relatively small surface area, spreads out as it travels out into space towards the satellite. You can observe the same effect using a battery-powered torch by shining the torchlight onto a wall. If you stand very close to the wall, the circle of light shining on the wall is relatively small. As you move further away from the wall, the circle of light becomes bigger, but you will notice that it also becomes somewhat dimmer. What is happening is that the same amount of light is distributed over a greater area. The solid angle subtended by a signal beamed out into space by a parabolic antenna will be a constant, but the surface area of its projection will be a function of distance (i.e. it will increase as the distance over which it is transmitted increases).

A microwave signal transmitted from a ground station is attenuated by distance
