The Indefinite Integral
The indefinite integral (also called the antiderivative, and sometimes the primitive integral) is related to the definite integral through the fundamental theorem of calculus - a topic we shall be exploring in some depth elsewhere in this section. We know that the definite integral will give us the area of the region under a curve for a continuous function over a closed interval. As such, it evaluates to a number. The indefinite integral does not evaluate to a number. Rather, the indefinite integral is a function. In fact, as we shall see, it is an entire family of functions with an infinite number of members.
The name antiderivative actually describes the nature of the indefinite integral quite well. It is, in essence, the opposite of the derivative. Suppose we have a function ƒ(x) for which we want to find the indefinite integral. We have already established that we are looking for a function. It turns out that ƒ(x) is actually the derivative of the function we are looking for. Let's look at an example. Suppose we want to find the indefinite integral of the function ƒ(x) = x 2 + 2x. We know that ƒ(x) is the derivative of the function we are looking for, but how do we reverse the process of differentiation in order to get the indefinite integral? Let's think about what we had to do to get the derivative in the first place.
Consider the term x 2. When we differentiate a power of x, we multiply the coefficient of x by the exponent to which x is raised, and then decrement the exponent by one. To reverse the process, we need to increment the exponent by one, and divide the coefficient of x by the new exponent. The new exponent of x will therefore be three (3), and the new coefficient of x will be one third (1/3). The integral of x 2 is thus 1/3 x 3. Applying the same procedure to the term 2x, we see that the integral of 2x must be x 2. The function we are looking for - which we'll call F(x) - will therefore be:
F(x) = 1/3 x 3 + x 2
If this is correct, then finding the derivative of this function should give us the original function ƒ(x) = x 2 + 2x. Applying the basic rules of differentiation to F(x) will confirm that this is the case:
F ′(x) = x 2 + 2x
In general terms, we can define the indefinite integral of ƒ(x) as any function F(x) such that:
F ′(x) = ƒ(x)
There is a potential problem here, however. Consider the following possibilities for F(x):
F(x) = 1/3 x 3 + x 2 + 5
F(x) = 1/3 x 3 + x 2 + √86
F(x) = 1/3 x 3 + x 2 + π
F(x) = 1/3 x 3 + x 2 + e 2
Now think about what the derivative will be for each of these functions. You will of course find that they will all have the same derivative, i.e.
F ′(x) = x 2 + 2x
Why? Because the last term in every case is a constant. Whenever we differentiate a constant, we get zero. It therefore doesn't really matter what constant term we have at the end of a function when differentiating. Any collection of functions that only differ from one another by a constant term will all have the same derivative. When you think about it, this is perfectly logical. Why? Because the derivative of a function simply gives us the slope of that function for a given value of x. Adding a constant value to a function does not change its slope, merely its vertical orientation. We can see this from the illustration below.
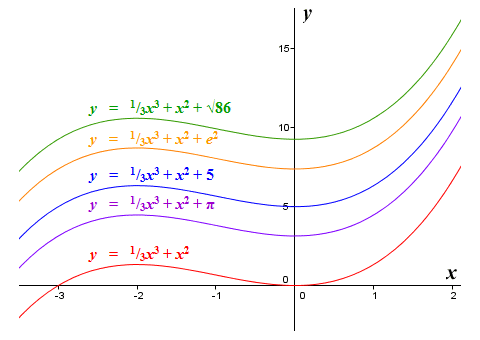
Adding a constant term to a function does not alter its slope
There are in fact an infinite number of functions that will give us exactly the same derivative. The only difference between them will be the constant term. We could therefore perhaps write the indefinite integral of the function ƒ(x) = x 2 + 2x as follows:
F(x) = 1/3 x 3 + x 2 + ?
where the question mark represents the unknown constant value. We'll come back to the question of how we deal with this unknown value shortly. Meanwhile, let's turn our attention to the notation we should be using here for the indefinite integral. You probably remember how to write a definite integral for a function ƒ(x):
| ∫ | b | ƒ(x) dx |
| a |
The integral symbol (that's the long 's' character over on the left-hand side) tells us that we are looking at an integral, and the subscripted and superscripted characters a and b immediately to the right of the integration symbol are the lower and upper limits of integration respectively. The function ƒ(x) is the integrand (i.e. the thing we are integrating), and the dx at the end tells us that x is our variable of integration (it can also be seen as representing infinitesimally small increments of x). Now look at how we write the indefinite integral of ƒ(x):
| ∫ | ƒ(x) dx |
At first glance, this looks the same as the notation for a definite integral. Note, however, that the upper and lower limits of integration are missing. This is because there is no domain of integration. Whereas the definite integral leads us to a number that represents the area of a bounded region under the graph of a function, the indefinite integral is simply another function - the function we get, in fact, by reversing the process of differentiation that gave us the function ƒ(x). This process, which is the inverse of differentiation, is called antidifferentiation (or indefinite integration).
We still need to do something about the constant term that was lost when we carried out our differentiation (to simplify things, we will work on the assumption that there was a constant term, even if there wasn't). There is of course no way to determine the value of the constant term. Once it has been eliminated in the differentiation process, it is gone for good. But how do we show this missing constant in our notation? The answer is actually very simple. We just use the letter C as a placeholder. Here is how we write the indefinite integral of the function ƒ(x) = x 2 + 2x:
| ∫ | x 2 + 2x dx = 1/3 x 3 + x 2 + C |
The letter C represents all possible values of the missing constant, including zero. We call C the constant of integration. The dx that follows the integrand is a differential. In fact, you should already be quite familiar with it from your study of differential calculus. It is very important, and must never be omitted. Why? Well for one thing, it tells us where the expression to be integrated (the integrand) ends. In the above example, its absence would not really cause a problem, but consider the following indefinite integral:
| ∫ | 3x 2 + 2x dx + 3 = x 3 + x 2 + C + 3 |
Suppose we forgot to include the dx on the left-hand side of the equation? Obviously, our notation would be incorrect. Of far more importance, though, is the fact that we would get the wrong answer, i.e.
| ∫ | 3x 2 + 2x + 3 = x 3 + x 2 + 3x + C |
There are other good reasons for always including the differential. For example, it tells us which variable we are integrating for (i.e. whether we are integrating for x, or for some other variable). This is particularly important if we wish to venture into the realms of multivariable calculus. Even if we never go further than single-variable calculus, we will inevitably encounter integration problems far more complex than the examples we have looked at so far. This will often involve manipulating equations using algebraic operations that rely on the presence of the differential.
Putting everything we have learnt so far together, we can now express the indefinite integral of a function ƒ(x) as follows:
| ∫ | ƒ(x) dx = F(x) + C |
where F(x) satisfies the condition that:
F ′(x) = ƒ(x)
Although we will talk about the fundamental theorem of calculus in much more detail elsewhere, it is worth briefly outlining the theorem here in order to give you an idea of how integration and differentiation are related, and why the indefinite integral can help us to calculate a definite integral for an integrable function. The theorem itself is in two parts. The first part, which is sometimes called the first fundamental theorem of calculus, essentially just tells us that integration and differentiation are the inverse of one another. The second part, which is sometimes called the second fundamental theorem of calculus, tells us that we can calculate a definite integral for a function using one of its indefinite integrals (of which, remember, there are an infinite number).
We have already seen an example of how we can apply the first part of the theorem to find the indefinite integral of a function, simply by applying the power rule for integration. This rule is essentially the inverse of the power rule used in differentiation. It is based on Cavalieri's quadrature formula, which is named after the seventeenth century Italian mathematician Bonaventura Francesco Cavalieri (1598-1647). The integration power rule formula is as follows:
| ∫ | ax n dx = a | x n+1 | + C |
| n+1 |
Note that n must not be equal to minus one (n ≠ -1) because this would put a zero in the denominator on the right hand side of the formula. The letters a and C represent the constant coefficient of x, and the constant of integration respectively. This rule on its own enables us to integrate all polynomial functions of one variable. As with differentiation, we integrate each term separately, and the plus or minus sign in front of each term does not change. More complex functions will require additional rules, which we will talk about elsewhere in this section. Integration has no equivalents for the product and quotient rules used in differentiation. If we encounter a product or a quotient in an integration problem, we need to find other ways of dealing with them.
The most important consequence of the second fundamental theorem of calculus is that it gives us a relatively straightforward way of evaluating a definite integral for a function. In a nutshell, it tells us that if a function is continuous over some closed interval, then the definite integral for that interval (or domain of integration) can be calculated by finding the values of the indefinite integral (which is a function, remember) at each end of the interval. The definite integral will be the difference between these two values. In other words, if the function F(x) is the indefinite integral of the function ƒ(x), and ƒ(x) is continuous over the closed interval [a, b], then:
| ∫ | b | ƒ(x) dx = F(b) - F(a) |
| a |
Let's try an example. We'll find the definite integral for the function ƒ(x) = 2x 5 - 10x 3 + 5 for -2 ≤ x ≤ 2. The graph of this function is shown below. As you can see, the definite integral will have both positive and negative components.
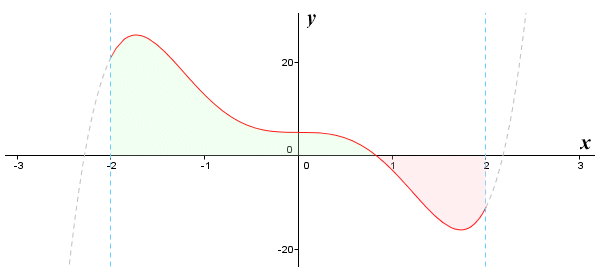
The graph of the function ƒ(x) = 2x 5 - 10x 3 + 5 for -2 ≤ x ≤ 2
Applying the power rule for integration to each term of the function in turn, we get the following:
| ∫ | 2x 5 dx = 2 | x 6 | = | 1 | x 6 |
| 6 | 3 |
| ∫ | -10x 3 dx = -10 | x 4 | = - | 5 | x 4 |
| 4 | 2 |
| ∫ | 5 dx = 5 | x | = 5x |
| 1 |
The indefinite integral F(x) for the function ƒ(x) = 2x 5 - 10x 3 + 5 is therefore given by:
| F(x) = | ∫ | 2x 5 - 10x 3 + 5 dx = 1/3 x 6 - 5/2 x 4 + 5x |
And the definite integral for the function ƒ(x) = 2x 5 - 10x 3 + 5 for -2 ≤ x ≤ 2 will be:
| ∫ | 2 | 2x 5 - 10x 3 + 5 dx = F(2) - F(-2) |
| -2 |
| ∫ | 2 | 2x 5 - 10x 3 + 5 dx = (211/3 - 40 + 10) - (211/3 - 40 - 10) |
| -2 |
| ∫ | 2 | 2x 5 - 10x 3 + 5 dx = -82/3 + 282/3 = 20 |
| -2 |
Which is the correct answer. If you ever need to check the result of your calculations, there are many online definite integral calculators you can use, like this one at the Number Empire website:
http://www.numberempire.com/definiteintegralcalculator.php
