Introduction

Integral calculus is one of the two major branches of calculus, the other being differential calculus. Both branches of calculus are concerned with measuring things that change in a non-linear way. Differential calculus is about finding the instantaneous rate of change of some quantity. Integral calculus is more concerned with how much something has changed over a specified interval. Suppose we we plot a graph of the speed of a motor vehicle travelling from point A to point B. The x axis represents time (the independent variable), and the y axis represents the speed of the vehicle (the dependent variable).Since the speed of the vehicle is bound to vary over time, the graph will be non-linear. The total distance travelled can be found by multiplying the average speed by the elapsed time. It can also be found by measuring the area under the graph. Consider the following illustration.

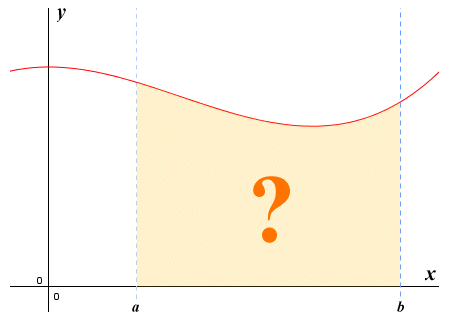
Integral calculus is about finding the area under a curve

Integral calculus is about finding the amount by which some quantity has changed according to some function. In order to do so, we need to find the area under a graph of that function between two points. But looking at the above illustration, how would we calculate the area of the shaded region under the curve between points a and b? If all of the lines forming the boundary of the region were straight, finding its area would be relatively easy. Unfortunately, despite being bounded by the x axis at the bottom and the vertical lines enclosing the interval [a, b], it has an irregular shape. There is no simple formula we can use to calculate the area of a shape like this. The good news is that integral calculus provides us with all the tools we need to solve exactly this kind of problem! We will be exploring some of those tools in this section.