The Cosine Function
Although the sine function is probably the most familiar of the six modern trigonometric functions, the cosine function comes a close second. Indeed, the sine and cosine functions are very closely related, as we shall see (if you are not familiar with the sine function, you may wish to read the page entitled "The Sine Function"). However, whereas the modern sine function is closely related to the chord function used by the ancient Greeks, the cosine function has no equivalent in Greek trigonometry. In fact, the Greeks had no other trigonometric functions apart from the chord. Nevertheless, they were aware of the association between the sine and the cosine functions, albeit not in a trigonometric sense. The way in which the two functions relate to each other is captured in geometric terms by the Pythagorean theorem, which defines the relationship between the sides of a right-angled triangle. Consider the illustration below.
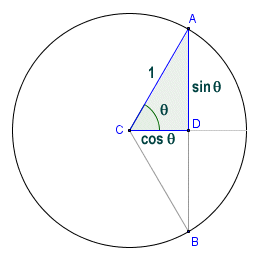
The relationship between sine and cosine
You should be able to see from the diagram that the half-chord AD is one leg of the right-angled triangle ADC. The other leg is line segment CD, which lies on the perpendicular bisector of chord AB. The hypotenuse AC of the right-angled triangle is a radius of the circle. The illustration shows a unit circle, which has a radius of one unit in length. The length of the half-chord subtending central angle θ will therefore have the same value as the sine of angle θ. Similarly, the length of the line segment joining the chord's mid-point to the centre of the circle will have the same value as the cosine of angle θ. Note that for a circle of arbitrary radius r, the length of line segment CD would be equal to cos (θ ) r. Just in case you are still a little uncertain about how all this works, let's revisit how the sine and cosine functions are defined in terms of a right-angled triangle.
Consider the right-angled triangle shown below. In any right-angled triangle, one of the internal angles will always be ninety degrees (90°). Since the internal angles in any triangle must always sum to one hundred and eighty degrees (180°), the other two internal angles must both be acute angles (i.e. less than ninety degrees). The side opposite the right-angle is always the longest side, and is called the hypotenuse. In relation to either one of the acute angles, the side opposite the angle is referred to as the opposite. The remaining side (the side common to both the angle in which we are interested and the right angle) is called the adjacent.
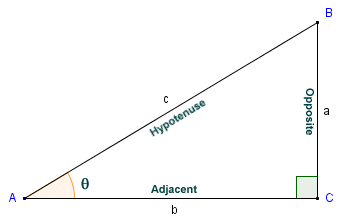
In triangle ABC, sin (θ ) = a/c and cos (θ ) = b/c
In triangle ABC, we are interested in angle θ. We have used the convention of labelling each vertex with an upper case character, and the side opposite each vertex with the corresponding lower-case character. The opposite in relation to angle θ is side a. The adjacent is side b, and the hypotenuse is side c. The sine of an angle in a right-angled triangle is defined as the quotient of the lengths of the opposite and the hypotenuse. Thus, in triangle ABC, the sine of angle θ is given as:
| sin (θ ) = | a |
| c |
The cosine of an angle in a right-angled triangle is defined as the quotient of the lengths of the adjacent and the hypotenuse. Thus, in triangle ABC, the cosine of angle θ is given as:
| cos (θ ) = | b |
| c |
In the illustration below, we show part of a unit circle with its centre at point A and a radius r = 1. We have extended line segment BC to a point D on the perimeter of the circle, so that line segment BD becomes a chord of the circle. In the right-angled triangle ABC the vertical leg, i.e. the half-cord subtending angle θ, represents the sine of angle θ. The horizontal leg represents the cosine of angle θ. You have probably also noted the fact that, with respect to angle θ, the legs corresponding to the sine and cosine are also the opposite and adjacent sides of the right-angled triangle respectively.
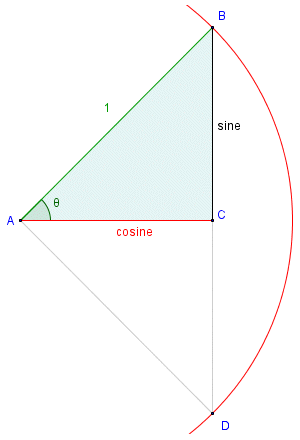
The sine and cosine are line segments of the unit circle
Look at this triangle, and think about what we know from Pythagoras' theorem. In a right-angled triangle, the square of the hypotenuse is always equal to the sum of the squares of the other two sides. In this case, since the length of the hypotenuse is one (1), then the square of the hypotenuse will also be one. From this, we can reason that the sum of the squares of the sine and cosine must be equal to one. Now, bear in mind that for any similar triangle (i.e. a triangle in which all of the angles are the same and the lengths of the sides are in the same proportion to one another) the sine and cosine values will not change, since they relate to the ratios of the sides to one another regardless of their lengths. Thus, from the Pythagorean theorem, we derive the following relationship between the sine and cosine of an angle θ:
sin2 (θ ) + cos2 (θ ) = 1
From the above equation, and looking at the representation of the sine and cosine as line segments in the unit circle, we can derive some other interesting facts about the relationship between the sine and cosine. First of all, we can re-arrange the equation in order to derive an expression for the sine of an angle in terms of its cosine, and vice versa:
sin2 (θ ) = 1 - cos2 (θ )
cos2 (θ ) = 1 - sin2 (θ )
Now look at the diagram again and consider how things would change if, instead of angle θ, we were interested in finding the sine and cosine of the other acute angle, i.e. angle ABC. Line segment AC now becomes the opposite, and by definition the sine of angle ABC. Line segment BC meanwhile becomes the adjacent, and by definition the cosine of angle ABC. Since the two acute angles in a right-angled triangle are complementary (i.e. they must add up to ninety degrees), we can derive the following relationships between the sine and cosine of angle θ:
sin (θ ) = cos (90° - θ )
cos (θ ) = sin (90° - θ )
Hence the sine of an angle is equal to the cosine of that angle's complement. For this reason, the cosine function is considered to be a co-function of the sine function (which is probably why it is called a cosine). If you have read the page entitled "The Sine Function", you may recall that each of the three main trigonometric functions (sine, cosine and tangent) is defined as the ratio of two of the sides of a right-angled triangle. As we saw above, the sides are labelled in accordance with the way in which they relate to the acute angle in which we are interested, and the trick is to remember which of the sides to use in order to calculate the value of whatever trigonometric function we want to find. So, just as a reminder, here once again is the (relatively) easy-to-remember mnemonic SOH-CAH-TOA, which should remind you that:
Sine = Opposite over Hypotenuse
Cosine = Adjacent over Hypotenuse
Tangent = Opposite over Adjacent
Thankfully, the days of having to use trigonometric tables to find the cosine of an angle (or the angle corresponding to a given cosine value) are long gone. Modern calculators can instantly perform the necessary calculations, providing you know how to use the calculator correctly. Nevertheless, for those interested in such things, we have used Microsoft Excel to produce our own table of cosines for angles ranging from zero degrees (0°) up to three hundred and sixty degrees (360°) in increments of one tenth of a degree. To see the table, click here.
Finding the cosine of an angle with the built-in calculator provided in Microsoft Windows is relatively straightforward. Let's assume we want to find the cosine of an angle of seventy-five degrees (75°). If you have it, start the Microsoft Windows built-in calculator by clicking on the start button in Windows 7 and selecting All Programs>Accessories>Calculator (other versions of Windows might require a different sequence of keystrokes). Select the scientific version of the calculator from the application's View menu. To find the cosine of seventy-five degrees using the Windows calculator, enter the following keystrokes (if you don't have the Windows calculator, use any available calculator that can perform trig functions):
Enter these keystrokes to find the cosine of seventy-five degrees
Make sure that you have the calculator set to the Degrees mode (unless you are planning to enter a value for the angle in radians or gradians). If you have entered the keystrokes correctly, you should now see the following display:
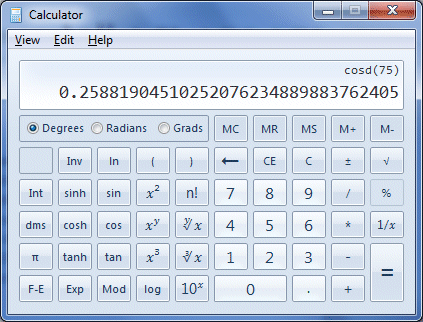
The calculator displays the value of cos (75°)
Now let's assume that you want to find the size of an acute angle in a right-angled triangle by first finding the quotient of the adjacent and hypotenuse (i.e. the angle's cosine). Providing you have values for the lengths of the sides of the triangle, you can find the value of the angle's cosine easily enough. Finding the angle is then simply a case of applying the arccosine function (which is the inverse of the cosine function) to the result. Let's find the value of angle θ for the right-angled triangle illustrated below.
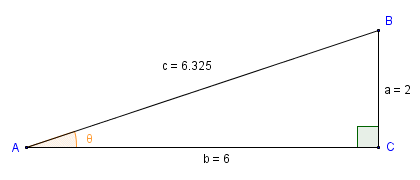
We want to find the size of angle θ
For angle θ, sides b and c are the adjacent and the hypotenuse respectively. We can actually find the size of the angle in a single operation on the Windows calculator. We do this by using brackets in the key sequence entered, in order to get the calculator to find the quotient of the adjacent and hypotenuse (i.e. the cosine of the angle) first. We then apply the arccosine function to the result. Here is the key sequence to use:
Enter these keystrokes to find the size of angle θ
If you have entered the keystrokes correctly, you should see the following display:
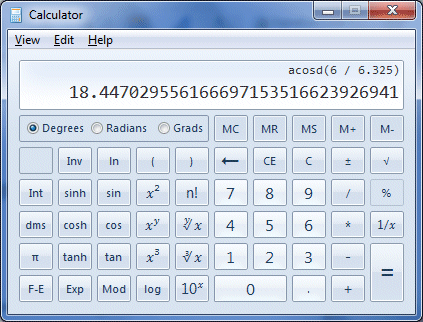
The calculator displays the value of angle θ
As with the sine function, we can apply the cosine function to angles of greater than ninety degrees. To see an interactive demonstration of how the cosine varies as the size of the angle changes, click here (note: your browser must support Java in order for the interactive page to work). The demonstration uses the unit circle to demonstrate how the cosine values vary with the angle of rotation. Note that the cosine is represented by the horizontal leg of a right-angled triangle. The vertical leg is the half-chord subtending the central angle in which we are interested, and also represents the sine. The hypotenuse is a radius of the circle, and is also the terminal side of the angle of rotation (the initial side being the positive x-axis).
As the angle of rotation increases beyond ninety degrees, the right-angled triangle moves into a new quadrant. The series of screen shots below illustrate the point (we have added the quadrant numbers to the screen shots for clarity). The unit circle has its centre (shown here as point O) at the origin of a Cartesian coordinate system, and a radius of one unit. The length of the vertical leg of the right-angled triangle at any point is therefore equal to the absolute value of the sine of the central angle subtended by the half-chord. Similarly, the length of the horizontal leg of the triangle is equal to the absolute value of the cosine of the central angle subtended by the half-chord.
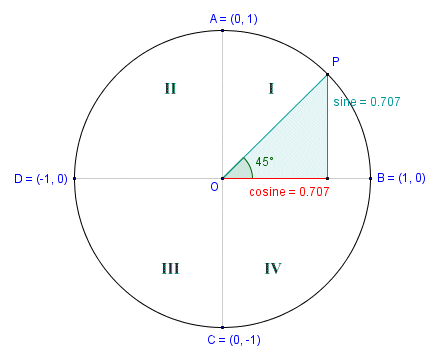
The cosine in quadrant I
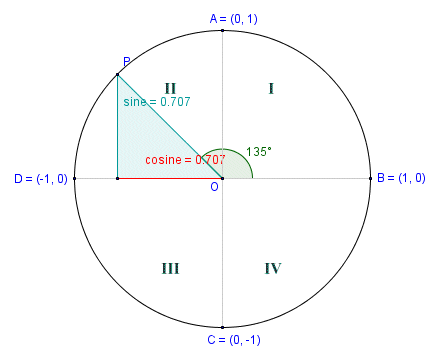
The cosine in quadrant II
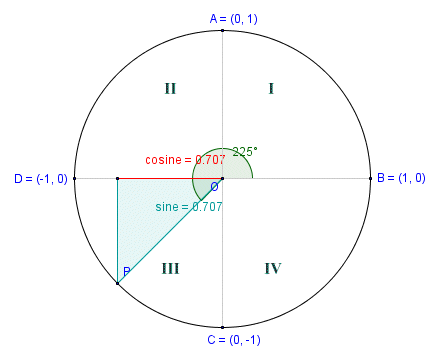
The cosine in quadrant III
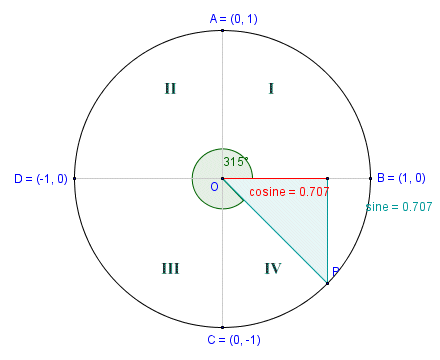
The cosine in quadrant IV
The angle of rotation in the first quadrant is forty-five degrees (45°), and is therefore the same as the angle subtended by the half-chord. In the second screenshot, we have increased the angle of rotation by ninety degrees to one hundred and thirty-five degrees (135°). The half-chord is now in the second quadrant, but the central angle subtended by the half-chord is once again forty-five degrees. We see the same thing in the third and fourth quadrants. The angle of rotation continues to increase as we move point P anti-clockwise around the circumference of the circle, but the central angle subtended by the half-chord in each quadrant will never exceed ninety degrees.
Both the sine and cosine trigonometric functions can be defined in terms of a point lying on the circumference of the unit circle. That point is the point at which the half-chord touches the circumference of the unit circle (point P on the diagrams shown above). The angle θ to which the cosine corresponds is the angle between the positive x-axis and the radius joining point P and the centre of the circle O, measured anti-clockwise. The cosine of this angle is defined to be the x-coordinate of point P. We can express this simply as:
cos (θ ) = x
Like the sine function, the cosine function has values in the range one to minus one (1 to -1). In the first and fourth quadrants (the quadrants to the right of the y-axis), those values will always be between zero and one, since x will always be equal to or greater than zero. In the second and third quadrants, (the two quadrants to the left of the y-axis), the values will always be between zero and minus one, since x will always be equal to or less than zero. The cosines of the angles zero degrees (0°), ninety degrees (90°), one hundred and eighty degrees (180°) and two hundred and seventy degrees (270°) will be one (1), zero (0), minus one (-1) and zero (0) respectively.
We saw above that in terms of the unit circle, the x and y coordinates of any point P on the circumference of the circle are given by the cosine and sine respectively of the angle between the positive x-axis and the line segment connecting the centre of the circle to point P, measured anti-clockwise. As we have seen, this line segment forms the hypotenuse of a right-angled triangle for which the cosine gives the length of the horizontal leg (sometimes referred to as the run), and the sine gives the length of the vertical leg (sometimes referred to as the rise). The tangent function, which we talk about elsewhere, gives the slope (i.e. the quotient of the rise and the run).
Both the sine and cosine functions are said to be periodic functions with a period of three hundred and sixty degrees (360°) or 2π, because the values returned by each function will be repeated after each complete cycle. This means that we can find the sine or cosine of any angle, no matter how large. A rotation of two and a half turns, for example, is equivalent to an angle of nine hundred degrees (900°). The sine and cosine would be given as:
sin (900°) = sin (900 (mod 360)°) = sin (180°) = 0
cos (900°) = cos (900 (mod 360)°) = cos (180°) = -1
The mod operator used here is short for modulus, and yields the remainder produced when one number is divided by another. In the example used here, we are dividing nine hundred by three hundred and sixty, which produces a remainder of one hundred and eighty. The periodic nature of the sine and cosine functions can be demonstrated graphically by plotting a graph of these functions against a range of angles, as illustrated below. Like the sine function, the cosine function is often used to model the behaviour of cyclic phenomena. A cosine wave represents a smooth, repetitive oscillation in exactly the same way that a sine wave does, except that (in terms of the unit circle) it is a graph of the way in which the value of x varies over time, rather than y.
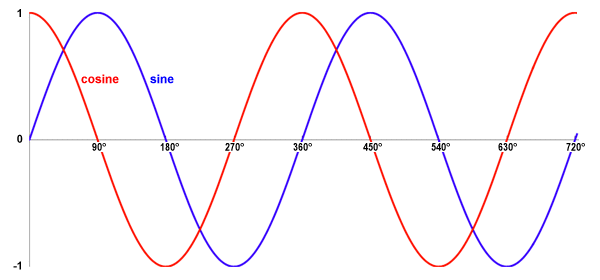
A graph of sine and cosine values plotted against angles from 0° to 720°
You can see from the graph that both the sine and cosine functions go through a complete cycle at three hundred and sixty degree intervals. You may also observe that the cosine wave is ninety degrees (90°) in advance of the sine wave. The cosine wave is thus said to lead the sine wave by ninety degrees. Apart from this obvious difference, the cosine wave is identical in shape to the sine wave and, like the sine wave, is often used to model the behaviour of cyclic phenomena. In its most basic form, a cosine wave is a function of time that is described by the formula:
x (t) = A · cos (ωt + φ)
where:
A = the amplitude of the function (the maximum absolute value of y)
ω = the angular frequency (usually measured in in radians per second)
t = the elapsed time
φ = the phase, i.e. the angle (in radians) when t = 0
The history of the cosine function is closely bound to that of the sine function. Indian mathematicians had developed the cosine function by the fifth century CE, which they used together with the sine function in the context of performing astronomical calculations. Their knowledge of the sine and cosine functions, along with the rest of their astronomical and mathematical knowledge, was subsequently acquired by Arab scholars as the Islamic empire expanded. Much of the work of these Arab scholars, translated into Latin and accompanied by the extensive trigonometric tables they had compiled, had found its way into Europe by the twelfth century CE.
By the end of the sixteenth century CE, European scholars had produced trigonometric tables which were accurate enough to be used for astronomical calculations even as recently as the early twentieth century. Somewhat more recent developments have included the development of various representations of trigonometric functions as infinite series. Without dwelling too much on the details, suffice it to say that values for the sine or cosine of many angles cannot be calculated using simple algebraic formulae. As with the sine function, the cosine function of an angle can only be accurately expressed as the result of adding together an infinite number of terms. One such representation gives the cosine of an angle x (expressed in radians) as:
| cos (x) = 1 - | x2 | + | x4 | - | x6 | + · · · |
| 2! | 4! | 6! |
Obviously, it is not practical, or even possible, to perform calculations using an infinite number of terms. The number of terms actually used will depend to a large extent on the computational resources available, and on the degree of accuracy required for the cosine value.
