The Scalar Triple Product
The scalar triple product, as the name suggests, is a way of multiplying three vectors together that gives a scalar value as the result. It actually combines the dot product and cross product operations in order to produce a scalar value using three vectors, which for the purposes of this discussion we will call vectors a, b and c. The scalar triple product of vectors a, b and c is written as (a b c), and is defined as:
(a b c) = a · (b × c)
You may occasionally see the parentheses omitted, since the cross product operator takes precedence over the dot product operator. The scalar triple product of vectors a, b and c is thus the dot product of vector a and the vector defined by the cross product of vectors b and c. Before we proceed further, it may be useful to consider what the scalar triple product of three vectors is not (and why). Consider the following arrangements involving three vectors and the dot product or cross product operators:
(a · b) · c
(a · b) × c
(a × b) × c
The first arrangement won't work because the dot product of vectors a and b will be a scalar value, and we cannot subsequently find the dot product of a scalar value and a vector. The second arrangement is also a non-starter because again, the dot product of vectors a and b will be a scalar value, and we cannot find the cross product of a scalar value and a vector. The third arrangement is perfectly feasible, since the cross product of vectors a and b will be a vector, and we can find the cross product of two vectors. This last arrangement is not what we are looking at in this page, however, and actually produces something called the vector triple product (another vector, rather than a scalar value).
The scalar triple product is frequently used in geometry to find the volume of a parallelepiped, which is a three-dimensional shape with six faces, each of which is a parallelogram. The three vectors may be seen as three adjacent edges of the parallelepiped, originating from a common vertex. The value of the scalar triple product, if non-zero, will be a positive value if vectors a, b and c are defined using a right-handed coordinate system, otherwise it will be negative. Obviously, when used to find the volume of a parallelepiped, the absolute (unsigned) value must be used regardless of the handedness of the coordinate system.
The scalar triple product is also a test of whether or not the three vectors are linearly independent. If the vectors are not linearly independent, the value of the scalar triple product will be zero. Linear dependence means that, for a given collection of vectors, at least one of the vectors can be duplicated by some combination of one or more other vectors in the collection (or multiples thereof). What this means is that, in order for our three vectors to be linearly independent, no more than two of the vectors can lie in the same plane, and the vectors that do lie in the same plane must point in different directions (i.e. they must be non-parallel).
Let's think about it another way. We said that the scalar triple product gives us the volume of a parallelepiped. If the scalar triple product has a value of zero, there is no parallelepiped, since a three-dimensional object cannot have a volume of zero. Consider the illustration below, which shows a parallelepiped. Three adjacent edges of the parallelepiped are formed by the vectors a = (1, 1, 1), b = (4, 2, 0) and c = (0, 2, -1). The x, y and z axes are included to show the orientation of the coordinate system used (in this case, a right-handed system).
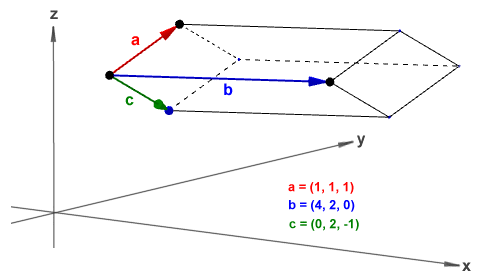
Vectors a, b and c form three adjacent edges of a parallelepiped
In order to find the scalar triple product of vectors a, b and c, we first need to find the cross product of vectors b and c. If you have read the page entitled "The Cross Product of Two Vectors", you will know that we can find the x, y and z components of the cross product vector (which for convenience we will call vector d ) using the x, y and z components of vectors b and c as follows:
dx = bycz - bzcy = (2)(-1) - (0)(2) = -2
dy = bzcx - bxcz = (0)(0) - (4)(-1) = 4
dz = bxcy - bycx = (4)(2) - (2)(0) = 8
We now need to find the dot product of vectors a and d. If you have read the page entitled "The Dot Product of Two Vectors", you will know that finding the dot product is straightforward if you know the x, y and z components of the two vectors, and is found as follows:
a · d = axdx + aydy + azdz = ((1)(-2)) + ((1)(4)) + ((1)(8)) = -2 + 4 + 8 = 10
We can also obtain the scalar triple product somewhat more directly using matrix arithmetic. The scalar product will be the determinant of a three-by-three matrix, each row of which will consist of the x, y and z components of one of the vectors. Row one will be the x, y and z coordinates of vector a, row two will be the x, y and z coordinates of vector b, and row three will be the x, y and z coordinates of vector c. The matrix for vectors a, b and c is shown below.
| ax | ay | az | ||
| bx | by | bz | ||
| cx | cy | cz |
The cross product vector is obtained by finding the determinant of this matrix. If you are unfamiliar with matrices, you might want to look at the page on matrices in the Algebra section to see how the determinant of a three-by-three matrix is found. Below is the actual calculation for finding the determinant of the above matrix (i.e. the scalar triple product of vectors a, b and c). Note that the determinant of a matrix is written in the same format as the original matrix, but instead of brackets, the columns are enclosed within vertical bars.
| (a b c) = a · (b × c) = | ax | ay | az | = ax | by | bz | - ay | bx | bz | + az | bx | by | |||||||||
| bx | by | bz | cy | cz | cx | cz | cx | cz | |||||||||||||
| cx | cy | cz | |||||||||||||||||||
Substituting actual values, we get:
| (a b c) = a · (b × c) = | 1 | 1 | 1 | = | 2 | 0 | - | 4 | 0 | + | 4 | 2 | ||||||||
| 4 | 2 | 0 | 2 | -1 | 0 | -1 | 0 | 2 | ||||||||||||
| 0 | 2 | -1 | ||||||||||||||||||
The calculation then becomes:
(a b c) = a · (b × c) = ((2)(-1) - (2)(0)) - ((4)(-1) - (0)(0)) + ((4)(2) - (0)(2))
(a b c) = a · (b × c) = -2 + 4 + 8 = 10
This gives us the same result that we had before, which is as it should be. Before we leave the scalar triple product, it is worth noting a couple of things about it. Firstly, the same result can be obtained using a different ordering of the vectors, providing the cyclic order in which they appear remains constant. This gives us the following equivalences:
(a b c) = (b c a) = (c a b) = a · (b × c) = b · (c × a) = c · (a × b)
Secondly, switching the two vectors in the cross product part of the scalar triple product expression negates the value of the scalar triple product (the absolute value remains the same, but the sign changes). This gives us the following:
(a b c) = (b c a) = (c a b) = - (a c b) = - (b a c) = - (c b a)
This translates to:
a · (b × c) = -a · (c × b)
b · (c × a) = -b · (a × c)
c · (a × b) = -c · (b × a)
In essence, any non-cyclic permutation causes the sign of the result to change.
