Acceleration, Freefall and Projectile Motion
Overview
We have seen that an object in an inertial frame of reference is either at rest or has a constant velocity (i.e. it moves at a constant speed in a straight line). In order for the object's speed or direction to change, it must experience a net force in some direction. The result of the net force acting on the object is called acceleration. An object that is accelerating due to a gravitational force, but has no other forces acting upon it, is said to be in free fall.
We can see examples of objects that are accelerating all around us. A train leaving a platform, a car pulling away from a set of traffic lights, an aircraft taking off, or an apple falling from a tree. We may even be fortunate enough to witness the launch of a NASA or ESA space mission. All of these things are examples of things that are accelerating. There are also some not so obvious examples of acceleration, most of which you can see in the night sky, either with the naked eye or with the aid of a telescope.
The Moon, for example, is accelerating, as are all of the World's orbiting satellites. This sounds like a contradiction in terms, especially considering that we use the term “geostationary” to describe many of these satellites, but we'll see in due course why it really is the case that these orbiting objects are accelerating.
What's even more interesting is that these same objects - the Moon and all of the man-made satellites - are also in free fall. Don't worry, though. They're not going to land on your head - at least, not any time soon. This simply means that the only force acting on them (and the reason they are in fact accelerating) is the force of gravity - primarily the gravitational force exerted on them by the Earth, although the orbiting objects themselves exert a gravitational force on the Earth (and each other) in proportion to their mass.
Acceleration
Acceleration describes the rate of change of velocity with respect to time. It could describe a change in either the magnitude of the velocity or the direction of the velocity, or both. Note that if the velocity's magnitude is changing, it is accelerating regardless of whether the magnitude is increasing or decreasing (we all speak colloquially about deceleration on occasion, but the term is not generally used by physicists). In mathematical terms, acceleration is the derivative of velocity with respect to time, and the second derivative of position with respect to time.
Acceleration is a vector quantity (it has both magnitude and direction). The SI unit of acceleration is metres per second per second or metres per second squared (m s-2). When a train standing at a platform in a station starts to move and gather speed, it accelerates in the direction of travel. We'll assume for the moment that once the train reaches its cruising speed and stops accelerating, it will maintain that speed. If the train then goes round a bend in the track, it will be accelerating towards a new direction.
If the train is moving in a straight line as it pulls away from the station, it is said to be undergoing linear acceleration. Passengers in the train will experience it as a force pushing them back in their seats. If the train goes round a bend at a constant speed, it is undergoing centripetal (or radial) acceleration. In this case, the passengers will experience a sideways force. When the train slows down again as it approaches the next station, passengers will experience acceleration in the opposite direction to the direction of travel, this time as an inertial force pushing them forwards in their seats.
Note that acceleration is not a measure of velocity. It tells you how fast the velocity is changing, but it doesn't tell you what the velocity is. If the acceleration acts in the same direction as the velocity, i.e. in the direction of motion, then the magnitude of the velocity will increase. This is what happens as our train leaves the station. If the acceleration acts in the opposite direction, i.e. against the direction of motion, then the magnitude of the velocity decreases. This is what happens as our train approaches a station.

Train passengers will experience acceleration as a force pushing them back in their seats as the train leaves the station
Photograph: Daniel Abadia
The acceleration of an object due to uniform circular motion (i.e. its centripetal acceleration), whether it is moving at a constant or varying speed, is due to something called the centripetal force. It is of course also possible that the train is increasing or decreasing its speed (a change in the magnitude of its velocity) at the same time it is going round a bend (a change in the direction of its velocity). If this is the case it would also be undergoing both centripetal and tangential acceleration. We'll come back to these topics in due course. For the moment, we'll concentrate on linear acceleration – specifically, the question of average acceleration versus instantaneous acceleration.
Average acceleration
If an object changes velocity at a constant rate, it is called constant acceleration. A body undergoing constant acceleration will have the same acceleration at any point in time. In other words, its instantaneous acceleration will be the same as its average acceleration. A stone dropped from the top of a cliff is good real-world example of constant acceleration. As soon as the stone is released, it starts to fall due to the effects of gravity.
After one second, the stone has increased its velocity from zero (0 m s-1) to ten metres per second (10 m s-1). After two seconds, its velocity has increased to twenty metres per second (20 m s-1), and after three seconds, it is thirty metres per second (30 m s-1). The rate at which the stone's velocity is changing is thus ten metres per second per second (10 m s-2).
Because the acceleration is uniform, the instantaneous acceleration will also be ten metres per second per second, which is the acceleration due to gravity at the Earth's surface. Actually, the acceleration due to gravity is slightly less than ten metres per second per second (it's closer to 9.8 m s-2), and we've ignored the effects of air resistance, but hopefully you get the general idea.
Acceleration will not always be constant, however. A train pulling away from a station, for example, will gather speed rapidly at first, but will gradually reduce the rate at which it increases its velocity as it approaches cruising speed. The illustration below shows a graph of velocity versus time for an object, initially at rest, accelerating to some maximum speed. For the purposes of this discussion, we'll assume that the object is travelling in a straight line.
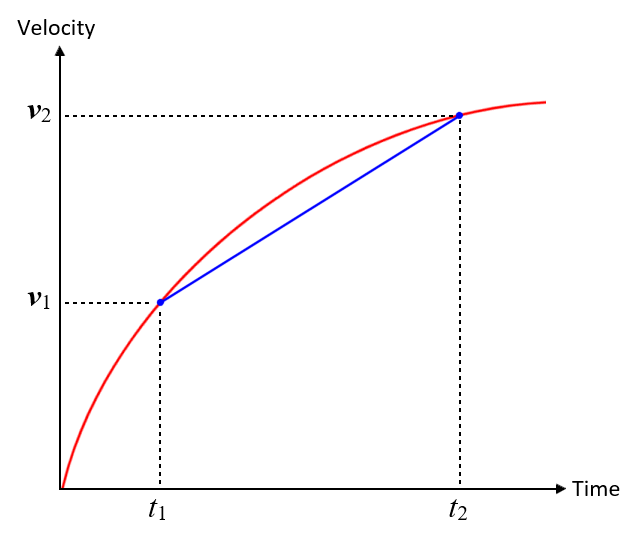
A velocity versus time graph for a moving object
As we stated above, acceleration is the rate of change of velocity with respect to time. The average acceleration of an object is thus equal to the change in velocity (Δv) in metres per second divided by the change in time (Δt) in seconds. We can therefore express average acceleration (ā) as:
| Average acceleration ā (m s-2) = | Change in velocity v (m s-1) | = | Δv |
| Change in time t (s) | Δt |
Suppose we want to find the average acceleration of an object during a given time interval. We'll call the start of the time interval t1, and the end of the time interval t2. The initial velocity and the final velocity will be v0 and v1 respectively. The average acceleration ā of the object will be the slope of the line segment connecting points (t1, v1) and (t2, v2) on our graph, and can thus be calculated as follows:
| ā = | Δv | = | v1 - v0 |
| Δt | t1 - t0 |
Instantaneous acceleration
As you no doubt realise, acceleration is not always uniform. Sometimes we want to know the instantaneous acceleration, i.e. the rate at which velocity is changing at a single instant in time. Let's look once more at the graph we saw above, which plots velocity against time for an object moving in a straight line and accelerating from rest to its maximum speed. This time, we are interested not in the average acceleration over some time interval, but in the instantaneous acceleration at time t.
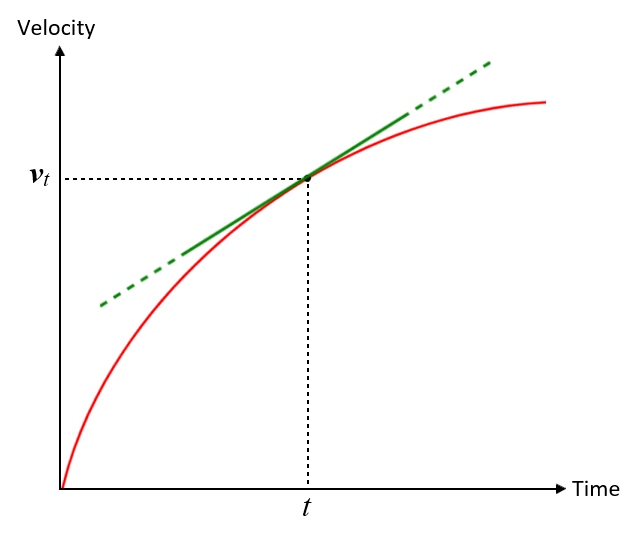
A velocity versus time graph for a moving object
What we are looking for here is the change in velocity over a time interval for which Δt approaches zero. The instantaneous acceleration a of the object will be the slope of the line that is tangent to the graph at time t. It is therefore, by definition, the derivative of velocity, as a function of time, at time t. The instantaneous acceleration can thus be defined as:
| a = | lim | Δv | = | dv |
| Δt→0 | Δt | dt |
Now, we know that acceleration is the rate of change of velocity with respect to time. We also know that velocity is the rate of change in position with respect to time. This means that acceleration is the rate of change of a rate of change. In mathematical terms, as we have already mentioned, acceleration is the derivative of velocity with respect to time and the second derivative of position with respect to time. We can express this relationship as follows:
| v = | dx | ⇒ a = | dv | = | d | ( | dx | ) | = | d2x |
| dt | dt | dt | dt | dt2 |
where x is displacement.
We can therefore find the instantaneous velocity in two ways. We can take the derivative of a velocity function, or we can take the second derivative of a position (displacement) function.
Uniform circular motion
An object moving along a circular path, such as a satellite orbiting the Earth, or a swinging pendulum, is undergoing acceleration by virtue of the fact that its direction of motion is constantly changing, even if its speed remains constant. It is said to be undergoing centripetal acceleration, i.e. acceleration directed towards the centre of the circle. The term is thought to have first been used by the English scientist and philosopher Isaac Newton (1642-1726]), and comes from the Latin centri, meaning "centre", and petere, meaning "to fall".
Centripetal acceleration is associated with centripetal force. This is the force required to make something move in a circle. It can take various forms, such as the tension in a rope or chain (think about the swings you played on as a child) or the force of gravity. Centripetal force is always directed towards the centre of the circular motion, i.e. along the radius of the circle, and is perpendicular to the tangential acceleration. It is a real force, and should not be confused with centrifugal force, which is a fictitious or apparent force (we'll talk more about that elsewhere).
Centripetal acceleration ac and tangential acceleration at are orthogonal (perpendicular to one another). Tangential acceleration is tangential to the circular path, and acts in a direction that is perpendicular to the centripetal acceleration. If an object is moving along a circular path at a constant speed, it is undergoing uniform circular motion. The tangential acceleration will be zero and the acceleration a will simply be the centripetal acceleration ac. Otherwise, a will be the result of adding the two vectors, ac and at. The diagram below illustrates the relationship.
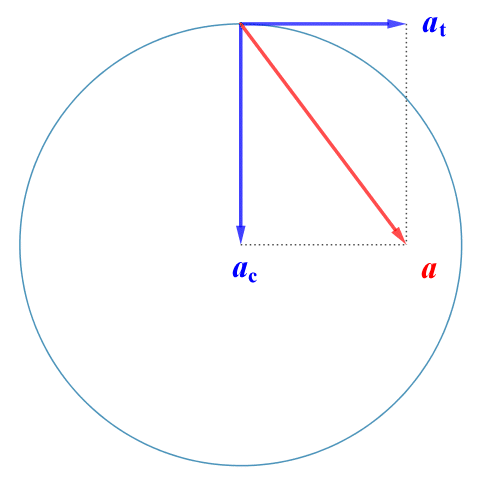
Centripetal and tangential acceleration are orthogonal
An object following a circular path thus has two components of acceleration. The tangential component at is due to a change in the magnitude of the velocity (i.e. speed). If speed is increasing, the tangential acceleration acts in the direction of the instantaneous velocity. If speed is decreasing, it acts in the opposite direction. The centripetal (or normal) component ac is due to the change in direction of the velocity vector, and acts perpendicular to the object's trajectory (i.e. along the radius) towards the centre of the circular path.
For the time being, we're just going to consider uniform circular motion, in which the object is moving at a constant speed v. There are (at least) two ways to do this. One of the methods we're going to look at is based on the geometry of a circle. The other takes a slightly more formal approach, using trigonometry and a little bit of calculus. We'll look at the geometrical approach first. Consider the following diagram:
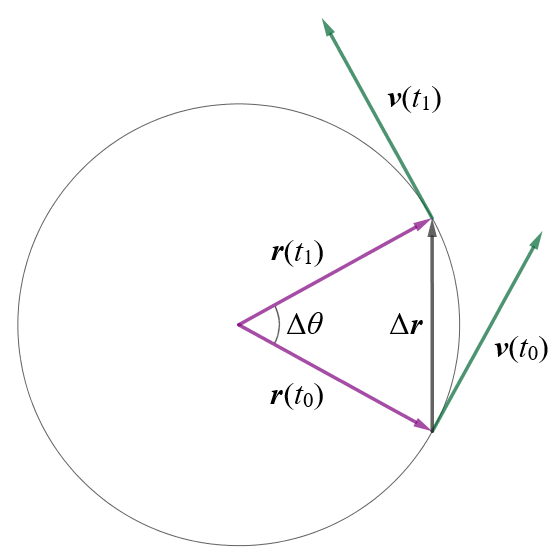
In circular motion, the direction of velocity constantly changes
Let's say we have a particle moving in an anti-clockwise direction along a circular path of radius r at a constant speed v. We have shown two velocity vectors for the particle, one at time t0 and one at time t1. The magnitude of each vector is the same, but each has a different direction because, at any point on the circular path, the instantaneous velocity must be tangential to the circle and perpendicular to the radius connecting that point to the centre of the circular motion.
Since velocity vector v(t0) is perpendicular to position vector r(t0) and velocity vector v(t1) is perpendicular to position vector r(t1), the triangle created by the vectors r(t0), r(t1) and Δr, and the triangle created by the vectors v(t0), v(t1) and Δv, are similar. And, since |r(t0)| = |r(t1)| = r and |v(t0)| = |v(t1)| = v, the triangles are isosceles (each triangle has two equal sides).
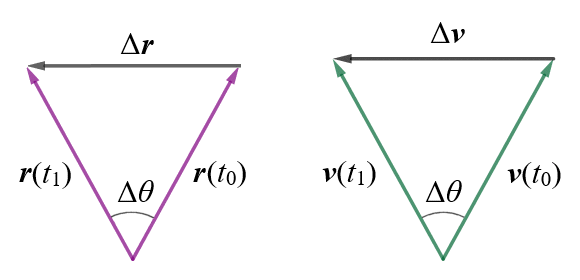
The triangles created by the position vectors and Δr, and the velocity vectors and Δv, are similar.
From the above, we can state:
| |Δv| | = | |Δr| |
| v | r |
Re-arranging, we get:
| |Δv| = | v | |Δr| |
| r |
Remember that
| |a| = | |Δv| |
| Δt |
therefore:
| |a| = | v | · | |Δr| |
| r | Δt |
As Δt tends to zero, however, the value of |Δr| will approach that of |Δv|
| lim | Δr | = | Δv | = v |
| Δt→0 | Δt | Δt |
therefore, the magnitude |ac| of the centripetal acceleration is given by:
| |ac| = | lim | Δv | = | v | ( | lim | |Δr| | ) | = | v2 |
| Δt→0 | Δt | r | Δt→0 | Δt | r |
where v is the particle's tangential speed.
But how do we prove that the acceleration always acts towards the centre of the circle? Here once more is the triangle formed by the vectors v(t0), v(t1) and Δv.
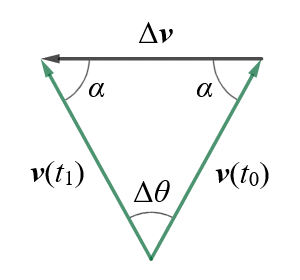
The triangle created by vectors v(t0), v(t1) and Δv
As we have already established, because the sides v(t0) and v(t1) are equal, the triangle is isosceles, and from our study of geometry we know that the angles opposite to the equal sides of an isosceles triangle are also equal (we have labelled them both α).
Remember that what we are interested in here is the direction of the instantaneous acceleration. As Δt gets smaller, the vectors v(t0) and v(t1) will get closer together, and angle Δθ will also get smaller. At the same time, since the internal angles of a triangle must always sum to 180°, each angle α will approach 90°. In the limit Δt→0, Δθ tends to zero, angle α tends to 90°, and Δv is thus perpendicular to v. Since v is tangent to the circle, Δv, which represents the direction of ac, points toward the centre of the circle.
* * *
The second approach we're going to use to derive a formula for centripetal acceleration involves trigonometry, and some calculus, but it's still relatively straightforward. We'll need to make use of a cartesian coordinate system in order to demonstrate this approach, and we'll be using the diagram below to illustrate the concept.
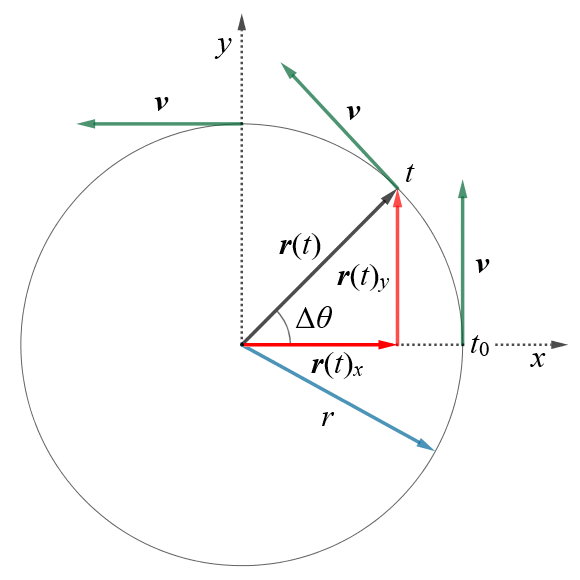
We can define circular motion in terms of a cartesian coordinate system
After time t, the position vector r(t) has rotated through an angle of Δθ with respect to the x-axis, and has a horizontal component, r(t)x, and a vertical component, r(t)y. At any time, t, the particle's position vector can be expressed as:
r(t) = r(t)x î + r(t)y ĵ
r(t) = r cos (Δθ) î + r sin (Δθ) ĵ
where î and ĵ are the unit vectors for the x and y axes respectively.
Since the speed of the particle moving along the circular path is constant, the angular velocity ω of the particle will also be constant:
| ω = | Δθ |
| t |
we can rearrange this to give the change in angle Δθ as:
Δθ = ωt
We can now re-write the position vector function as:
r(t) = r cos(ωt) î + r sin(ωt) ĵ
Since acceleration is the rate of change of velocity, let's now think about the instantaneous velocity of the particle, which we find by differentiating the position vector function to give us the velocity vector function (note the use of the chain rule here - the inner function of both terms to the right of the equals sign is ωt, so differentiating the inner function gives us ω):
| v = | dr | = -ωr sin(ωt) î + ωr cos(ωt) ĵ |
| dt |
In order to find the instantaneous acceleration a, we need to differentiate the velocity vector function:
| a = | dv | = -ω2r cos(ωt) î - ω2r sin(ωt) ĵ |
| dt |
Remember that what we are ultimately looking for here is the centripetal acceleration, i.e. the magnitude and direction of the acceleration acting towards the centre of rotation. We'll begin by finding the magnitude of the vectors, starting with r(t):
|r(t)| = √r2cos2(ωt) + r2sin2(ωt)
|r(t)| = r
Now we'll find the magnitude of v:
|v| = √(-ωr)2 sin2(ωt) + (ωr)2 cos2(ωt)
|v| = ωr
And finally, the magnitude of a:
|a| = √(-ω2r)2 cos4(ωt) - (ω2r)2 sin4(ωt)
|a| = ω2r
However, we know that the magnitude of a velocity vectors v is the speed v, so:
v = |v| = ωr
Therefore:
| ω = | v |
| r |
And the magnitude of a can be written as:
| |a| = | v2 | r = | v2 |
| r2 | r |
Which is the same result we arrived at using the geometric approach. We just need now to find the direction in which the acceleration a is acting. As we saw above:
a = -ω2r cos(ωt) î - ω2r sin(ωt) ĵ
We can factor out the -ω2 to give the following:
a = -ω2 (r cos(ωt) î + r sin(ωt) ĵ)
We also saw the following result above for position vector r(t):
r(t) = r cos(ωt) î + r sin(ωt) ĵ
So, we can express the acceleration a as:
a = -ω2 [r(t)]
The minus sign here indicates that the direction of the acceleration vector a is acting in the opposite direction to position vector r(t), because ω2 will always have a positive value. And, since position vector r(t) always points away from the centre of rotation and towards the particle wherever it is on the circular path, the acceleration vector must always point in the opposite direction, i.e. away from the particle's position on the circular path and towards the centre of rotation. Since the angular velocity of the particle is constant, there is no tangential acceleration, which means that:
ac = a = -ω2 [r(t)]
Non-uniform circular motion
As we have seen, an object moving along a circular path at a constant speed is undergoing uniform circular motion. The only form of acceleration experienced by the object is centripetal acceleration. If the speed is not constant, we have non-uniform circular motion. We now have angular acceleration, so in addition to the centripetal acceleration, the object is also exhibiting transverse, or tangential, acceleration. The diagram below shows the velocity and acceleration vectors for an object moving in an anti-clockwise direction along a circular path, in uniform circular motion (left), and in non-uniform circular motion (right).
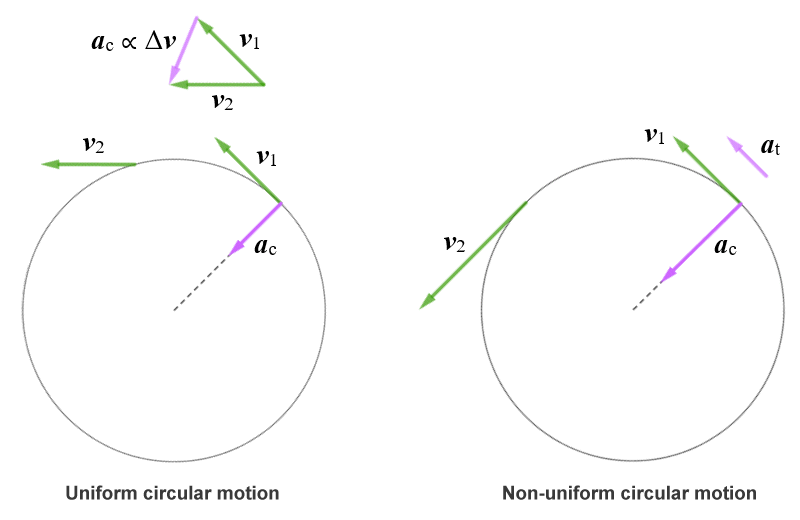
Non-uniform circular motion has both centripetal and tangential acceleration
An object moving along a circular path will always have centripetal acceleration. If the object's angular velocity is changing, the object will also have tangential acceleration. If the angular velocity is increasing, the tangential acceleration is a positive vector - it acts in the direction in which the object is moving. If the angular velocity is decreasing, it is a negative vector, and acts in the opposite direction.
The magnitude of the centripetal acceleration will also change during non-uniform circular motion. As we saw above, the magnitude of the centripetal acceleration ac of an object moving along a circular path is equal to the square of its tangential speed v divided by the radius r of the circular path:
| |ac| = | v2 |
| r |
So, if the object's angular velocity increases, its tangential speed, and hence the magnitude of the centripetal acceleration, also increases. If on the other hand the object's angular velocity decreases, both its tangential speed and the magnitude of the centripetal acceleration will also decrease.
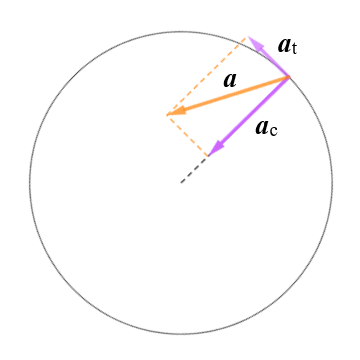
Our object now has two components of acceleration - a centripetal acceleration vector ac and a tangential acceleration vector at - that are perpendicular to one another. The object thus has a total linear acceleration vector, a, which is the vector sum of the centripetal and tangential acceleration:
a = ac + at
The principle is illustrated by the following diagram.
Total linear acceleration is the vector sum of centripetal and tangential acceleration
From the above, then, we can see that the magnitude of the total linear acceleration can be found using Pythagoras' theorem as follows:
|a| = √ac2 + at2
We already have an expression for the centripetal acceleration, ac, but we now need one for the tangential acceleration at. Since what we're looking at here is essentially just linear acceleration along a circular path, then the average tangential acceleration can be expressed as follows:
| āt = | Δv | = | v1 - v0 |
| Δt | t1 - t0 |
We have also already seen that the magnitude of the instantaneous acceleration can be taken by taking the derivative of velocity, as a function of time, at time t. In most cases, we can assume that the tangential acceleration is uniform, in which case the above formulae will be sufficient to allow us to calculate both the magnitude of the instantaneous tangential acceleration and that of the instantaneous total linear acceleration at time t1.
At this point it may help to clarify the difference between angular acceleration and tangential acceleration. Angular acceleration, represented by the lower-case Greek letter alpha (α), is an angular quantity expressed in radians per second per second (rad s-2). It is the rate of change of angular velocity ω per unit time.
| α = | Δω | = | ω1 - ω0 |
| Δt | t1 - t0 |
Tangential acceleration at is a linear quantity expressed in metres per second per second (m s-2). A body undergoing non-uniform circular motion has a tangential acceleration that is equal to the product of the angular acceleration and the radius of the circular path r. We can express this relationship as follows:
at = rα
When we talk about uniform circular motion, we are not usually concerned about the angle of rotation at any given time, since there is no angular acceleration. The only acceleration that occurs is centripetal acceleration, which acts from the current position of the rotating object towards the centre of the circular path. Once we start to look at non-uniform circular motion, we have both centripetal and tangential acceleration.
We now have two components of acceleration that are perpendicular to one another. At any given instant, the resulting linear acceleration is acting, not in the direction of the centre of rotation, nor in the direction of travel of the object, but somewhere in between. One way in which we can specify the direction in which the total acceleration is acting at a given instant is to calculate the angle φ between the acceleration vector a and the centripetal acceleration vector ac. Consider the following diagram, which shows an enlarged portion of the diagram we saw above:
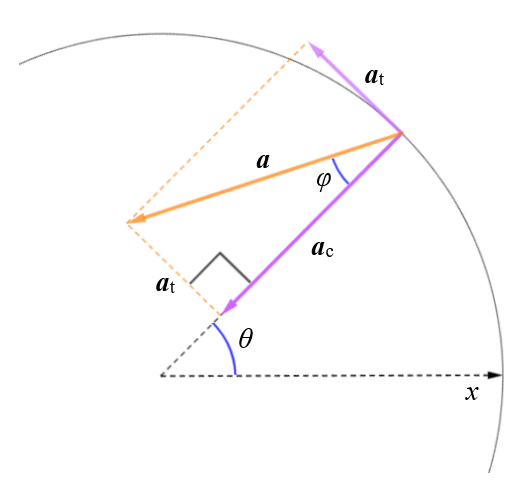
A right-angled triangle is formed by the vectors a, ac and at
The vectors a, ac and at will form a right-angled triangle in which the opposite and adjacent sides are represented by at and ac respectively (we achieve this by moving the tail of at to the head of ac). From trigonometry, we know that the tangent of an angle in a right-angled triangle is defined as the quotient of the lengths of the opposite and the adjacent. Once we have the tangent, we can find the angle by taking its arctangent (arctan or tan-1). The calculation is therefore as follows:
φ = arctan (at ÷ ac)
In order to find the direction in which the acceleration is pointing in terms of a polar coordinate system, we need to find the angle between the polar axis (in this case, the x-axis in the positive direction) and the total linear acceleration vector a. This will be equal to θ + 2π - φ or θ + 2π + φ (depending on whether the direction of rotation is clockwise or counter clockwise, and whether the acceleration is positive or negative).
* * *
There are a number of other ways of finding the centripetal, tangential and total acceleration of an object in non-uniform circular motion. Let's look at one involving unit vectors, as we did for uniform circular motion. We saw earlier that we can specify the position vector for an object in uniform circular motion within a cartesian coordinate system using the unit vectors î and ĵ for the x and y axes respectively, and we know that the centripetal acceleration at any instant acts in the opposite direction, from the object towards the centre of rotation. Once we begin to consider non-uniform circular motion, we need two additional unit vectors - the polar coordinate unit vectors ur and uθ.
All of the unit vectors have a magnitude of one. The purpose of the unit vectors is to specify direction, as we saw earlier. The unit vectors î and ĵ specify the x and y direction respectively, and as such are fixed. By contrast, the radial unit vector ur always points in the same direction as the position vector r(t) for an object moving along a circular path. It is defined in terms of the angle between r(t) and the polar axis (in this case the x-axis), in the counter-clockwise direction. The tangential unit vector uθ acts perpendicular to ur, and specifies the direction in which θ is increasing at a given instant. The unit vectors ur and uθ are thus constantly changing as the object moves along its circular path.
The following diagram illustrates the relationship between the unit vectors and the position vector r(t).
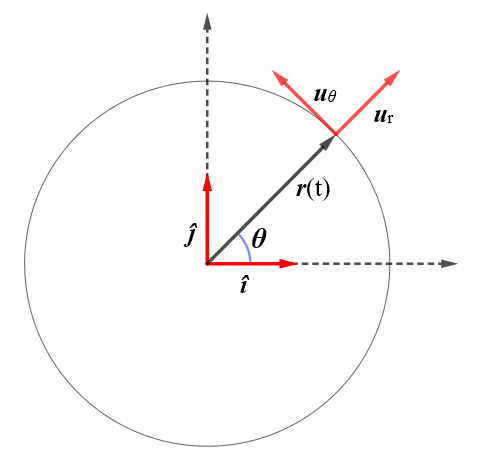
The position vector r(t) and the unit vectors î, ĵ, ur and uθ
The polar unit vectors can be expressed in terms of the cartesian unit vectors as follows:
ur = cos θ î + sin θ ĵ
and
uθ = -sin θ î + cos θ ĵ
We can define the position vector r(t) in terms of the radial unit vector ur:
r(t) = rur
where r is the radius of the circle (a constant).
What we're ultimately looking for is the acceleration, which is the rate of change of velocity, so we'll start by finding the instantaneous velocity. We find the instantaneous velocity by differentiating the position vector function to give us the velocity vector function:
| v = | dr | = r | dur | = r | d | (cos θ î + sin θ ĵ) |
| dt | dt | dt |
| v = r | dθ | (-sin θ î + cos θ ĵ) |
| dt |
| v = r | dθ | uθ |
| dt |
v = rωuθ
Note that, because r is a constant, we can move it to the left of the derivative in accordance with the constant coefficient rule. We have also substituted the expression cos θ î + sin θ ĵ for ur because, whereas ur is a polar unit vector that changes direction with time, î and ĵ are fixed Cartesian vectors that are independent of time. In the second line we have applied the chain rule, since θ here is a function of time. Since -sin θ î + cos θ ĵ is the definition of ur, we have simply replaced it in line three. The last line reflects the fact that dθ/dt is the angular velocity, ω.
This result is as expected. The velocity is acting tangentially to the circular path, and has a magnitude of rω. To get the acceleration, however, we need to differentiate again (this time using the product rule):
| a = | dv |
| dt |
| a = r | ( | dω | uθ + | duθ | ω | ) |
| dt | dt |
Note that:
| duθ | = | d | (-sin θ î + cos θ ĵ) |
| dt | dt |
| duθ | = | dθ | (-cos θ î - sin θ ĵ) |
| dt | dt |
| duθ | = - | dθ | ur |
| dt | dt |
| duθ | = -ωur |
We can thus write the total acceleration a as:
| a = r | ( | dω | uθ - ω2ur | ) |
| dt |
And the centripetal and tangential components of the acceleration are thus:
| ac = - ω2ur = - | v2 | ur |
| r |
and
| at = r | dω | uθ = | dv | uθ |
| dt | dt |
Freefall
An object is said to be in free fall if the only force acting on it is a gravitational force. Put another way, any object that is being acted upon solely by a gravitational field can be said to be in free fall. We used the example of a stone being dropped from the top of a cliff above to illustrate how an object will undergo a constant acceleration under the influence of a gravitational field. This example works well enough because the stone is small and dense, and the distance involved is relatively small. The effects of air resistance are therefore insignificant and can safely be ignored.
The same is not true for a larger and less dense object falling through the atmosphere from a much greater height. The classic example of what many people refer to as “free fall” is that of a skydiver descending from a high altitude (having jumped out of a perfectly serviceable aircraft - something I would never do!). At first, the speed at which the skydiver falls will steadily increase due to the pull of the Earth's gravitational field. The faster the skydiver falls, however, the more air resistance they will encounter.

A skydiver will encounter increasing air resistance as their speed of descent increases
Photograph: Kamil Pietrzak
Air resistance - sometimes referred to as drag - is the frictional force that an object experiences as it moves through the atmosphere. The moving object collides with gas particles in the atmosphere (mostly nitrogen and oxygen molecules) which impede the object's motion. The larger the surface area over which these collisions take place, and the faster the object is moving, the greater the resistance will be. In fact, we have all experienced air resistance when attempting to walk against the wind on a windy day!
In the case of a skydiver, a point is quickly reached where the upward force due to drag is equal to the downward force exerted by gravity. The skydiver's rate of descent will no longer be increasing, and from that point onwards they will be falling at a constant velocity (this is known as the terminal velocity). The use of the term free fall, then, does not really apply to a skydiver in a physics context, because gravity is not the only force acting on the skydiver. Objects orbiting the Earth, on the other hand, such as man-made satellites and the Moon, are in free fall.
The terminal velocity for a falling object will depend on several factors, including the mass and relative surface area of the object, the drag coefficient, and the height from which the object begins its descent. For a skydiver in the arch (or belly down) position, where the arms and legs are spread out to enable a stable attitude to be maintained, the terminal velocity is typically around 53 metres per second (195 kilometres per hour). An object will only achieve its terminal velocity if it falls from a sufficient height; a skydiver requires about 12 seconds to reach their terminal velocity, by which time they will have fallen approximately 450 metres.
Conjecture about why objects fall to the ground started thousands of years ago. The Greek philosopher Aristotle (384-322 BCE) was of the opinion that each of the four elements (earth, air, fire and water) had a natural place in the order of things, and that things formed from these elements had a tendency to migrate towards that natural place. Water returns to the sea, fire rises towards heaven, objects made of earth or stone fall to the Earth, and so on.
The Italian philosopher, astronomer and mathematician Galileo Galilei (1564-1642) carried out numerous experiments to determine the nature of bodies in motion. He is famously alleged to have dropped two cannonballs, differing from one another in both size and mass, from the top of the Leaning Tower of Pisa in order to demonstrate that they would both fall at the same rate, regardless of their respective masses. Whether this experiment actually took place is the subject of some debate; nevertheless, Galileo correctly determined that a freely falling body will accelerate uniformly, at a rate that does not depend on its mass.

Galileo allegedly dropped cannonballs from the top of the Leaning Tower of Pisa
Newton's theories concerning gravity were allegedly inspired by an apple falling on his head, which apparently led him to the conclusion that the force that compelled an apple to fall to the ground, and which appeared to be directed towards the centre of the Earth, was the same force responsible for holding the Moon in its orbit around the Earth. Newton's musings in this respect later led him to the conclusion that gravity - which he called "universal gravitation" - was responsible for the orbital motions of all of the planets in the solar system.
Closer to home, we are primarily interested in free fall in terms of how it affects the acceleration of a falling body that is relatively close to the Earth's surface, in the absence of other forces such as air resistance. The acceleration due to gravity at the Earth's surface is denoted by the symbol g, and is officially defined as:
g = 9.80665 m s-2
Note that the acceleration due to gravity is not uniform over the entire surface of the Earth. It is greater at the poles than at the equator; it is also greater at sea level than at high altitudes, and there are small regional variations due to geological factors. The figure given above is the nominal average value - sometimes referred to as standard gravity - at the Earth's surface.
The Earth's atmosphere does of course provide considerable resistance to falling objects that are light, or that have a large surface area. A deployed parachute is an example of an object that is both light and presents a large cross-sectional area in order to maximise the effects of air resistance. On the other hand, if an object is sufficiently heavy, has an aerodynamic shape, and is only falling a relatively short distance, then the effects of air resistance will be negligible and the object may be considered to be in free fall for most practical purposes.
The illustration below shows the velocity-time graph of an object in free fall, starting from a position of rest, and ignoring the effects of air resistance. The object's initial velocity is zero. After ten seconds, the object's velocity has increased to 98.1 metres per second, and its displacement from the rest position (i.e. the distance through which it has fallen) is 490.5 metres (we have assumed an acceleration due to gravity of 9.81 m s-2). The concave up shape of the graph tells us that the object has a positive acceleration, i.e. velocity is increasing. The slope of a line tangent to the graph at any time t represents the instantaneous velocity (vt) of the object at time t.
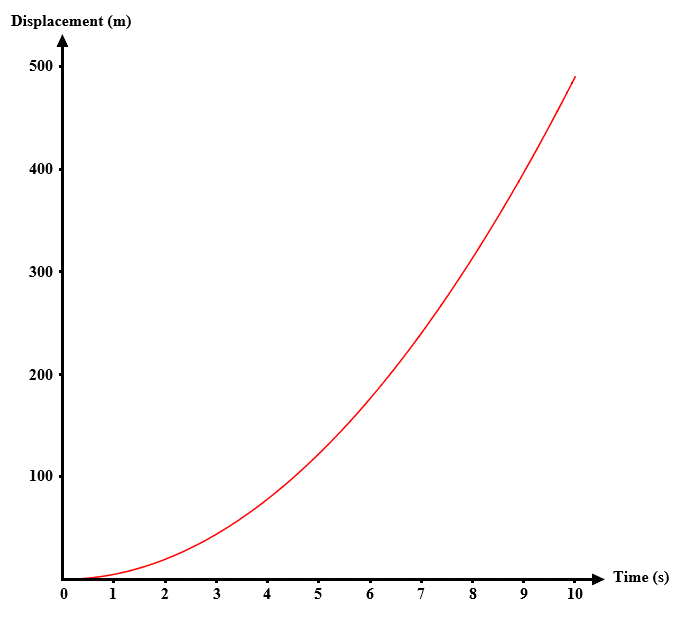
A velocity-time graph of an object in free fall
The distance through which a free-falling object falls (i.e. its displacement) will depend on the acceleration due to gravity g, the elapsed time t, and the initial velocity of the object (if the object starts from a rest position, the initial velocity will be zero). Note that an object can be in freefall even if it is initially moving in an upwards direction (think of a ball thrown high into the air). For an object moving in an upward direction, velocity and displacement are positive. If the object is falling, velocity and displacement will be negative.
Acceleration can be considered to be constant if we ignore factors like air resistance and variations in the gravitational field due to altitude and geographical location. Remember, however, that the acceleration due to gravity is always acting in the downwards (i.e. negative) direction, regardless of whether the object is moving upwards or downwards.
We'll consider the behaviour of objects that are following a parabolic trajectory when we look at projectile motion. For now, let's just consider motion in one dimension, i.e. objects that are moving in a straight line up or down. This simplifies things, because for an object that is dropped from a rest position, we know that its initial velocity is zero, and that once it has been released it will be in free fall (we'll also ignore the effects of air resistance). The most commonly used formulae relating to an object in free fall are:
v = v0 – g t
| y = y0 + v0 t + | g t 2 |
| 2 |
v 2 = v0 2 - 2g (y - y 0 )
where:
v = velocity (m s -1)
g = acceleration due to gravity (9.81 m s -2)
t = time (s)
y = vertical displacement (m)
The fact that two objects with very different masses will accelerate at the same rate under the influence of a uniform gravitational field in a vacuum was demonstrated in a dramatic way on the surface of the Moon by astronaut David Scott during the Apollo 15 Moon mission in 1971. Scott released a rock hammer and a feather at the same time, and from the same height. The items fell at the same rate, and landed on the lunar surface simultaneously, despite the difference in mass. The same experiment on Earth would have to be carried out in a vacuum.
Projectile motion
Projectile motion is the motion of a body (the projectile) that is projected into the air from some point close to the surface of the Earth. Examples of projectiles that demonstrate projectile motion could include an arrow fired from a bow, an artillery shell, a mortar bomb, or a ball thrown into the air. The study of projectile motion is called ballistics.

Soldiers of the Royal Artillery firing 105mm Light Guns during an exercise
Photograph: Ministry of defence
In addition to his observation that objects of different mass will fall to Earth from a position of rest at the same rate, Galileo also correctly surmised that the motion of a projectile was subject to movement in two principle directions simultaneously. As well as movement in the horizontal direction, the projectile was also moving in the vertical direction. He expressed this concept in his book Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica (or Dialogues Concerning Two New Sciences), in which he states:
"It has been observed that missiles and projectiles describe a curved path of some sort; however no one has pointed out the fact that this path is a parabola."
Once a projectile has been set in motion, the only force acting on it will be the Earth's gravitational field (for the purposes of this exercise, we will assume that the effects of air resistance are negligible). The gravitational force acts downwards towards the centre of the Earth, giving the projectile a downward acceleration. As Galileo pointed out, apart from the special case of a projectile that is launched vertically, the projectile will follow a parabolic curved path (we call this path a trajectory). The horizontal component of the projectile's motion is due to its inertia, and no additional external force is needed to maintain it.
A number of factors will determine the maximum height attained by a projectile, the amount of time it remains in the air, and the horizontal distance it will travel before landing. The most important factors are the initial velocity of the projectile, the angle at which it is launched, and the acceleration due to gravity. Other factors include wind speed, the effects of air resistance (as previously mentioned), and the nature of the terrain over which the projectile must fly. Depending on just how far the projectile is likely to fly, the curvature of the Earth's surface could also be a significant factor.
For the purposes of this discussion, we will assume that the effects of air resistance and wind speed can be ignored, that the terrain over which the projectile must fly is level, and that the distances involved are not sufficiently great that we need to take the curvature of the Earth into consideration. Bear in mind, however, that for practical applications of ballistics such as naval gunnery, artillery ranging, archery, or firearm related outdoor target sports, one or more of these factors must often be considered.
When we want to plot the trajectory of a projectile we can deal with the vertical motion and the horizontal motion separately, since they are essentially independent of one another. The horizontal component of velocity will be determined by the initial velocity of the projectile and the angle at which it is launched, and will remain constant throughout the duration of the projectile's flight. The launch angle θ is the angle between the direction in which the projectile is moving at the moment it is launched and the horizontal plane.
The vertical component of velocity is also determined by the initial velocity of the projectile and the angle at which it is launched, but will not remain constant throughout the duration of the projectile's flight because gravity is acting in the negative (downwards) direction. The upward motion of the projectile will slow and momentarily stop before it begins to fall back towards the Earth's surface at an increasing rate.
Let's consider the example of an artillery shell fired from a field gun at various angles. The initial velocity of the projectile will be the velocity at which the shell leaves the barrel of the gun, i.e. the muzzle velocity. Obviously different types of field gun have different muzzle velocities, but for argument's sake we'll assume that it's a fairly light gun with a muzzle velocity of 150 metres per second (150 m s -1). The graphic below shows the trajectories taken by a shell fired from the field gun at various angles of elevation.
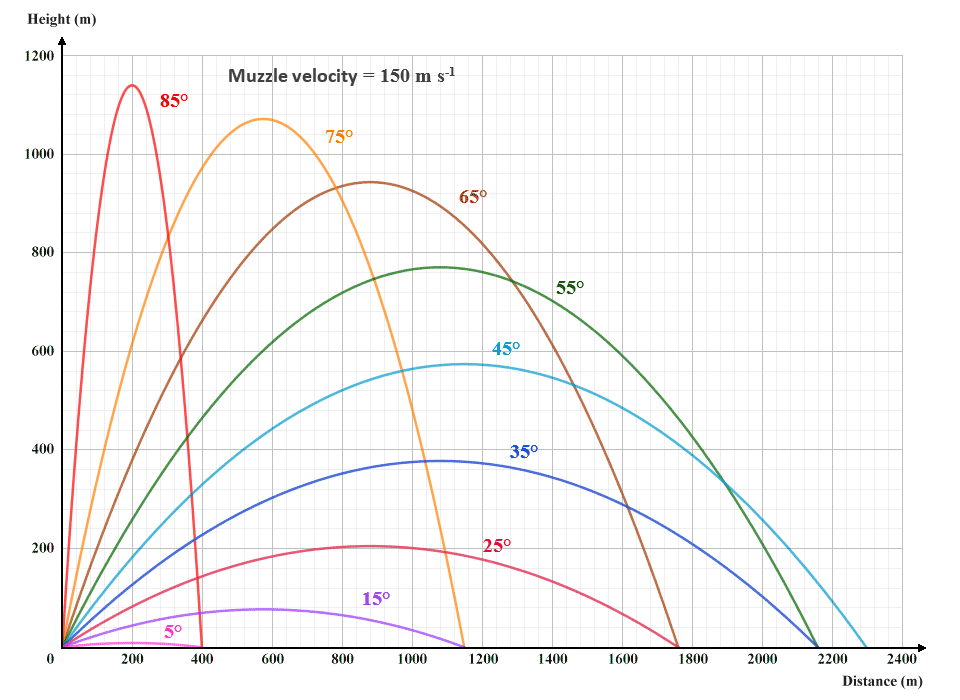
The path of a projectile is determined by launch angle and initial velocity
Before we start looking at the formulae used to analyse projectile motion, let's think about what the above graphic tells us. The first thing we should probably state is that we are considering motion in two dimensions only; the trajectory followed by our projectile has a horizontal component and a vertical component, but that's it. In many real-world situations (archery or outdoor target shooting, for example) we might need to take the effects of things like a cross-wind into account, and we would then be looking at motion in three dimensions. But let's keep things (relatively) simple.
What we can see straight away from the graphic is that for a projectile launched at a given initial velocity, both the maximum height attained and the horizontal distance travelled by the projectile will depend on the angle at which it is launched, which can be anywhere from zero to ninety degrees. The steeper the angle, the greater the maximum height.
The horizontal distance travelled by the projectile is called the range, which can vary somewhat depending on the terrain over which the projectile flies. We will work on the assumption that the point at which the projectile lands lies in the same horizontal plane as the location from which it is launched. The maximum range is achieved when the launch angle is exactly 45 degrees. At elevations above or below this angle, range decreases. In fact, as shown in the illustration, two projectiles launched with the same initial velocity but at complementary angles (angles that sum to 90 degrees), will have the same range.
The last thing to consider is the flight time - the time interval between the moment the projectile is launched and the moment it reaches the ground. This will depend on the height attained by the projectile, which is dependent upon the launch angle and initial velocity. The steeper the launch angle, and the higher the initial velocity, the higher the projectile will fly, and the longer it will remain in the air. The launch angle is important here, because it determines the magnitude of the vertical component of velocity.
Remember that the only force acting on the projectile is the downward force due to Earth's gravitational field. The negative acceleration due to gravity is constant and does not depend on the launch angle, so the greater the projectile's initial speed in the upward direction, the longer it will take to slow down, and the higher it will go. The illustration below shows how a shell fired from our field gun at various angles will behave in the time domain - we've plotted the height of the shell as a function of time. The total flight time in each case can be determined by looking at where the right-hand end of the curve meets the horizontal axis.
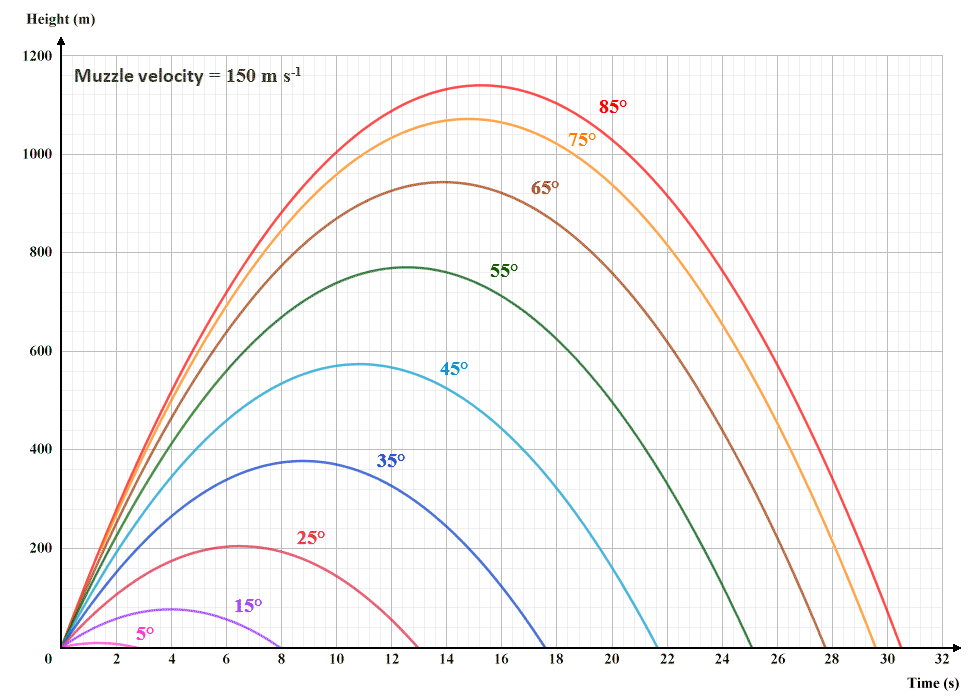
The flight-time and maximum height of a projectile is dependent on launch angle and initial velocity
Projectile motion formulae
There are numerous formulae that can be used to analyse projectile motion, depending on what we already know and what we want to know. In the majority of cases, we will be given the initial velocity and launch angle. The acceleration due to gravity g can usually be considered to be a constant (g ≈ 9.81 m s -2). We might also be required to base our calculations on the projectile being launched from a specific point in the two-dimensional plane, in which case we will be given the initial x and y coordinates. From these parameters, we can calculate:
- the horizontal component of velocity
- the initial vertical component of velocity
- the range of the projectile
- the maximum height reached by the projectile
- the flight time of the projectile
- the path length of the projectile's trajectory (i.e. the length of the parabolic arc)
- the velocity of the projectile at some time interval after launch
- the displacement of the projectile at some time interval after launch
We can also derive a function that describes the complete trajectory of the projectile, as well as being able to calculate the "angle of reach" to be used (assuming a fixed initial velocity) to achieve a specific range, or the initial velocity needed (assuming a fixed launch angle) to achieve a specific range. Note that, in most cases, initial velocity is the parameter most likely to be fixed (for example, the muzzle velocity of a projectile weapon).
The variables we can use in our calculations are summarised below (note that different sources may use different symbols for some of these variables; the angle of launch, for example, can denoted by either θ or α (the lower-case Greek letters theta and alpha respectively).
- x and y are the horizontal and vertical coordinates of the projectile respectively, and denote its position relative to the origin (0) in a two-dimensional coordinate system. The position can be expressed as a coordinate pair (x, y), and by convention the origin usually has the coordinates (0, 0). If the projectile is launched from a point other than the origin, the launch coordinates are usually represented by x0 and y0 , otherwise it is usually safe to assume that the projectile is launched from the origin.
- vx and vy are the horizontal and vertical components respectively of velocity v. The initial velocity is designated as v0 , and the horizontal and vertical components of the initial velocity are represented by v0x and v0y . As we have already mentioned, since there are no forces acting on the projectile in the horizontal direction, the horizontal component of velocity remains constant throughout the projectile's flight (vx = v0x ).
- θ is the angle of launch, i.e. the angle between the direction in which the projectile is moving at the moment it is launched and the horizontal plane. The launch angle can be expressed in either radians or degrees (1 radian ≈ 57.2958 degrees).
- R is the maximum range of the projectile, in metres. The calculation of range is based on the premise that the point at which the projectile lands lies in the same horizontal plane as the location from which it is launched.
- H is the maximum height attained by the projectile, in metres.
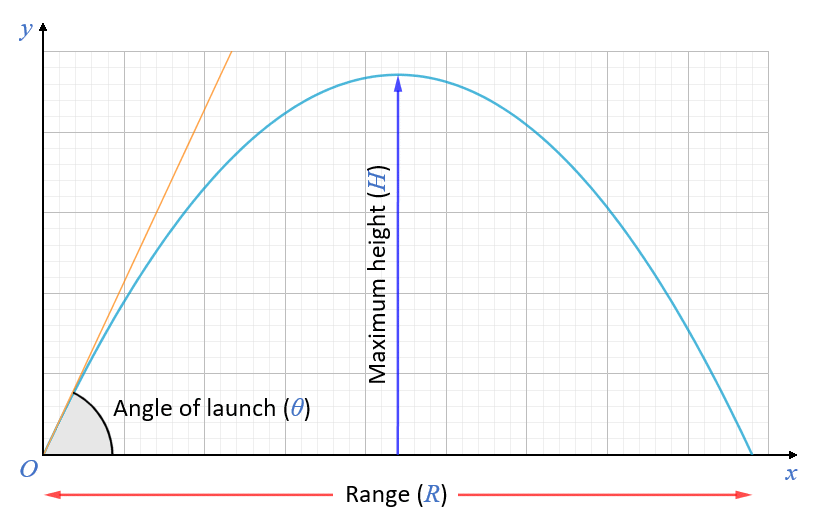
The range R and maximum height H are dependent on the initial velocity v and the angle of launch θ
- t is the time, in seconds, that has elapsed since the launch. Time dependent variables include the x and y coordinates of the projectile at any point on its trajectory.
- T is the total flight time of the projectile in seconds. As for range, the calculation of flight time assumes that the point at which the projectile lands is in the same horizontal plane as that from which it is launched.
- s is the displacement vector for the projectile at time t where t ≤ T. The magnitude of the displacement is expressed in metres.
- Φ is the displacement angle at time t where t ≤ T, i.e. the angle between the displacement vector and the horizontal plane. The displacement angle can be expressed in either radians or degrees. Note that at the instant the projectile is launched, the displacement angle is equal to the launch angle.
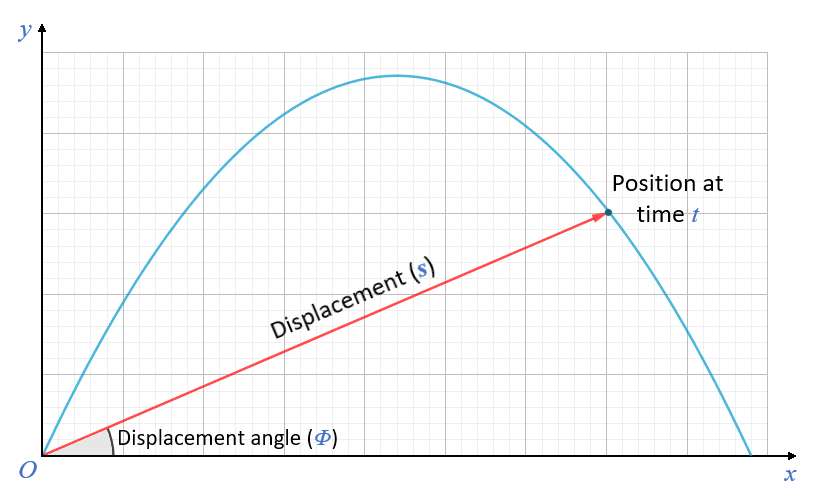
The displacement vector s points to the position of the projectile at time t
Some of the formulae used to analyse projectile motion are listed below.
Initial components of velocity:
v0x = v0 cos θ
v0y = v0 sin θ
Components of velocity: [0 < t ≤ T]
vx = v0x = v0 cos θ
vy = v0y - g t
Magnitude of velocity:
|v| = √vx 2 + vy 2
Position coordinates: [0 ≤ t ≤ T]
x = x0 + v0 t cos θ
| y = y0 + v0 t sin θ - | 1 | g t 2 |
| 2 |
Magnitude of displacement:
|s| = √x 2 + y 2
Displacement angle:
Φ = tan -1 (y/x)
Maximum height:
| H = | v0 2 sin 2 θ |
| 2g |
Range:
| R = | v0 2 sin 2θ |
| g |
Flight time:
T = 2v0 sin θ g
Trajectory path:
| y = tan θ x - | ( | g | ) | x 2 |
| 2v0 2 cos 2 θ |
Angle of reach for specified initial velocity and range:
For a shallow trajectory:
| θ = | 1 | sin -1 | g R |
| 2 | v0 2 |
For a steep trajectory:
| θ = | 1 | cos -1 | g R |
| 2 | v0 2 |
Note that, as we have mentioned previously, complementary angles will achieve the same range for a given initial velocity. The angle chosen for a given application will depend on factors such as the terrain. Whereas a shallow trajectory reduces flight time and thus lessens the effects of air resistance and cross winds, obstacles such as hills may necessitate the use of a steep trajectory in order to take the projectile over the obstacles (this is sometimes the case for a long-range artillery bombardment, for example).
From projectile to orbital motion
A projectile launched horizontally has no initial vertical component of velocity. In fact, the projectile will not travel very far at all if launched horizontally unless it is launched from some height. A cannonball fired horizontally from a cannon mounted atop a castle wall or some other elevated position would travel some distance before striking the ground, but a cannonball fired horizontally from a cannon standing on level ground would strike the ground almost immediately.
The range R and flight time T of a projectile launched horizontally will depend upon the height H from which it is launched and its initial velocity v0 , assuming that the terrain over which the projectile flies is level. If this is indeed the case, and over relatively short distances, the relevant calculations are as follows:
| R = v0 | √ | 2H |
| g |
| T = | √ | 2H |
| g |
If the range is large enough by comparison with the circumference of the Earth, the Earth's surface curves away below the path of the projectile, and the acceleration due to gravity changes direction. The range will be significantly greater than that predicted by the range formula given above, because the projectile must fall further before it reaches the ground.
It has been estimated that on average, the Earth curves approximately 5 metres downward for every 8000 meters along its horizon. It is often not possible to see this effect on land because the terrain tends to be uneven and there are often obstacles in the way. The effect can be quite noticeable, however, if you stand on the seashore and look out to sea. A point on the surface 8 kilometres away is effectively 5 metres lower than the point where you are standing, and distant ships will disappear below the horizon as they move away from you.
Given that the acceleration due to gravity is approximately 10 metres per second per second, a projectile will fall roughly 5 metres in one second. A horizontal velocity of 8000 metres per second close to the surface of the Earth would keep the projectile in orbit around the Earth, because the surface of the Earth continually falls away from the projectile. The mean orbital velocity needed to maintain a stable low Earth orbit is about 7.8 kilometres per second, but the requirement decreases with altitude. A low Earth orbit (LEO) satellite at an altitude of 200 kilometres, for example, has an orbital speed of 7.79 kilometres per second.
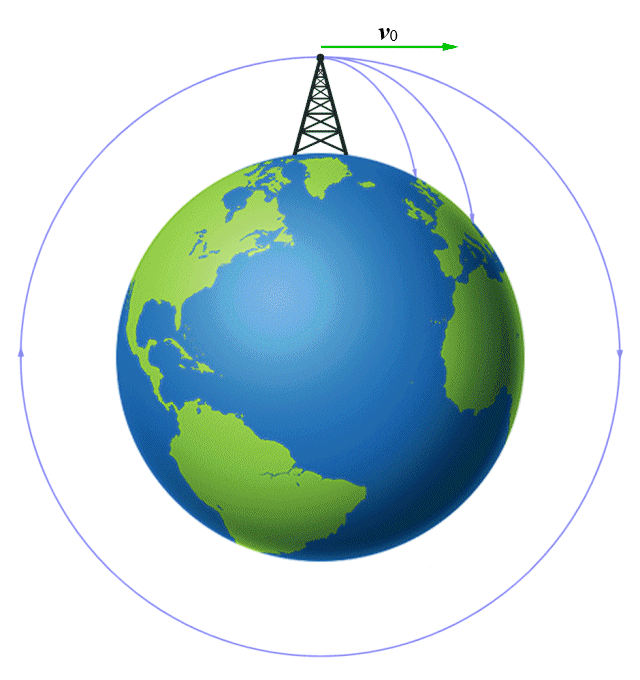
A projectile launched from a high tower with a sufficiently large initial velocity can achieve orbit
Note that the tower from which the projectile is launched must be tall enough to ensure that air resistance is not a significant factor (the lowest LEO satellites orbit at a height of around 160 kilometres).



