About Time
The story so far ...
Like most of the quantities we talk about in this section, time is one of the base quantities defined by the International System of Units. The internationally agreed base unit for time is the second. Common sub-multiples of the second include the millisecond (one millisecond is equal to one thousandth of a second) and the microsecond (one microsecond is equal to one millionth of a second). For historical reasons, most commonly used multiples of the second are not based on powers of ten. For example, the minute and the hour are time intervals consisting of sixty seconds and three thousand six hundred seconds (or sixty minutes) respectively.
Time is sometimes called the fourth dimension (the first three being the three spatial dimensions, typically referred to using a combination of three labels chosen from the terms length, width, height, depth and breadth). Man has always been aware of the passage of time. This is hardly surprising when you think about it. The passing of days is marked by the appearance of the Sun in the morning and its disappearance in the evening, while the passage of the years can be determined from the shortening and lengthening of the days, seasonal changes in the weather, the flowering of trees and plants, and the breeding cycles and migratory behaviour of birds and animals. Over many tens of thousands of years, Man's observations of the movements of the Sun, Moon and stars provided the basis for establishing a calendar, and for telling the time of day.
The history of time measurement is a long one. There is evidence to suggest that prehistoric peoples recorded the phases of the moon as long as thirty thousand years ago. Establishing a calendar has always been important to us, because our very survival depends upon being able to predict the seasons. Primitive man lived in hunter-gatherer societies that moved around from place to place, and relied primarily on foraging for nuts and berries, fishing, and hunting wild animals for food. This could often become difficult or impossible in winter, so food had to be gathered, preserved, and stored before the arrival of the snow and ice.
Eventually man learned how to domesticate wild animals and grow crops, and began to live in permanent settlements. The development of an agrarian society would not have been possible without a detailed knowledge of the seasons. In cooler regions, crops had to be sown at the right time of year and harvested before the onset of winter, and flocks of sheep and cattle had to be brought in from pasture and sheltered from the harsh winter weather. Even in lands that were warm all year round, it was important for farmers to be familiar with annual rainfall patterns and seasonal flooding. The calendar evolved out of a need to mark such events.
The ability to tell the time accurately grew in importance as man began to venture further from home and explore the world around them. Navigating the seas, far from land and with no familiar landmarks to guide them, sailors were able to determine their latitude (i.e. the distance north or south of the equator) by measuring the angular height of the Sun at mid-day. Navigators would measure their latitude when they left port on a voyage. For the return journey, they would sail north or south until they attained that latitude, then simply turn right or left as appropriate, and sail along the line of latitude until they reached their home port. Unfortunately, there was no way to accurately determine longitude (a measure of how far east or west one is from a given location).
By the eighteenth century, the accumulated astronomical observations of many centuries together with the development of powerful telescopes made it possible for astronomers at the Greenwich observatory to compile accurate charts and almanacs that gave the positions of the Sun, Moon and stars in the sky at various times throughout the year. A skilful navigator could use this information to find his longitude with a reasonable degree of accuracy, provided he was able to calculate the current time at the Greenwich observatory - a calculation that involved measuring the angular distance between the Moon and a known star or planet and comparing the result to a table of "lunar distances" compiled by the Greenwich observatory (for a more detailed explanation of how these calculations were made, see the article "A Brief History of Navigational Instruments" elsewhere in this section).
Navigation became much easier once reliable and accurate marine chronometers became available. These timekeeping devices could be synchronised to Greenwich time, reducing the number of calculations navigators had to make. This made the task of calculating one's position both more accurate and less time consuming. Today, of course, the Global Positioning System (GPS) enables anybody with a GPS-enabled device to establish both their position (accurate to within a few metres), and the current time, from virtually anywhere in the world - providing, of course, they can establish a line of sight with at least three GPS satellites.
The need for precise time measurement has grown with the development of industrialised societies. Modern transport and communication systems are highly dependent on accurate timekeeping. Timing is also a critical component in many industrial and manufacturing processes, as well as in most commercial endeavours. In scientific research, the availability of accurate of timekeeping apparatus is essential for the successful outcome of many experiments. And of course, we all live our lives according to schedules, with set times to get up, go to work or school, eat meals, or watch our favourite TV show (on demand TV notwithstanding, of course). The central heating system in your home, your washing machine, tumble dryer and dishwasher, your microwave oven, and the ignition system in your family car are all controlled by timers of one kind or another.
An instrument used to measure time is usually called a clock, although we refer to small portable versions designed for personal use as watches. The name "clock" is thought to come from the Celtic words clocca and clogan, both of which mean "bell". You probably consult a watch or a clock several times each day in order to determine when to get up, when to go to school, college or work, when to eat, or when to go to bed, as well as for many other purposes. You may well have used a stopwatch to see how long it takes to run a certain distance, or an egg-timer to ensure that your eggs are cooked just the way you like them.
Most if not all of our modern technological wonders are only possible because we can create increasingly accurate clocks and timing devices. The first commercial personal computer was the Altair 8800, which was produced in 1975 and used an Intel 8080 processor with a "clock speed" of two megahertz (two million cycles per second). Modern processors typically have clock speeds of several billion cycles per second. Computers and other electronic devices rely on these internal clocks in order to ensure that they can carry out their computational operations. Such operations must occur in discrete steps, in the correct order, thousands of millions (or even billions) of times per second.
And of course, we must ensure that all of our clocks, and the countless systems that depend on accurate timekeeping, remain synchronised. In order to achieve this, we need a reliable point of reference. This exists in the form of an international group of atomic clocks that define Coordinated Universal Time (UTC). The National Physical Laboratory (NPL) in Teddington, London, operates a caesium fountain clock (a type of atomic clock) that currently serves as the United Kingdom's primary frequency and time standard. Following recent improvements, this clock is now considered to be so accurate that it will lose or gain less than one second over a period of one hundred and thirty eight million years! In the United States, a similar clock called NIST-F1 is operated by the National Institute of Standards and Technology in Boulder, Colorado, and provides the primary frequency and time standard for the US.
Some common units of time
| Unit | Duration | Comment |
|---|---|---|
| Planck time unit | 5.39 × 10 −44 seconds | The time taken by light to travel one Planck length |
| yoctosecond | 10 −24 seconds | |
| zeptosecond | 10 −21 seconds | |
| attosecond | 10 −18 seconds | The shortest time period currently measurable |
| femtosecond | 10 −15 seconds | |
| picosecond | 10 −12 seconds | |
| nanosecond | 10 −9 seconds | |
| microsecond | 10 −6 seconds | |
| millisecond | 10 −3 seconds | |
| second | 1 second | The SI base unit for time |
| minute | 60 seconds | |
| hour | 60 minutes | |
| day | 24 hours | |
| week | 7 days | |
| megasecond | 10 6 seconds | Approximately 11.6 days |
| month | 28-31 days | |
| year | 12 months | |
| common year | 365 days | |
| tropical year | 365.24219 days (avg.) | Also knows as a solar year |
| Gregorian year | 365.2425 days (avg.) | |
| Julian year | 365.25 days | |
| sidereal year | 365.256363004 days | The time it takes for the earth to orbit the Sun once with respect to the fixed stars |
| leap year | 366 days | |
| decade | 10 years | |
| gigasecond | 10 9 seconds | Approximately 31.7 years |
| century | 100 years | |
| millennium | 1,000 years | |
| terasecond | 10 12 seconds | Approximately 31,700 years |
| petasecond | 10 15 seconds | Approximately 31.7 million years |
| exasecond | 10 18 seconds | Approximately 31.7 × 10 9 years |
| zettasecond | 10 21 seconds | Approximately 31.7 × 10 12 years |
| yottasecond | 10 24 seconds | Approximately 31.7 × 10 15 years |
The calendar
From the dawn of civilisation, man cannot have helped noticing that certain types of event would occur repeatedly, and at similar time intervals. The appearance and disappearance of the Sun marked the passing of days, the phases of the moon followed a regular pattern over a period of about twenty-nine days, and the days were longer during the summer and shorter during the winter. Ancient peoples observed the passage of the Sun, Moon and stars across the heavens. They recorded their observations, and gradually developed an extensive knowledge of the relationship between the lengths of the days and the position of the stars and constellations in the night sky.
It is thought that the concept of dividing a circle into three hundred and sixty degrees may have originated with the Babylonians, who discovered that the position of the sun with respect to the celestial sphere changes by approximately one degree of arc each day. The Babylonians used a sexagesimal number system (i.e. a number system based on the number sixty), and may have chosen the number three hundred and sixty because it was more convenient to work with than three hundred and sixty five. In any event, they recorded a vast amount of information relating to the movement of the stars and planets, the cycles of the sun and the moon, and the timing of lunar and solar eclipses. These records clearly showed that the events unfolding in the night sky throughout the year were cyclic, and provided the basis for the development of a calendar.
There is evidence to suggest that lunar calendars were in use some six thousand years ago, with the year divided into either twelve or thirteen lunar months. An extra month would have been added to some years to compensate for the fact that a full year (which we now know is about three hundred and sixty-five and a quarter days) is significantly longer than a year consisting of twelve lunar months. It is believed that this may be the reason why the numbers twelve and thirteen are significant in many cultures, even today. Archaeological evidence suggests a lunar calendar was used in China as long ago as 2000 BCE, although there is also evidence of a Chinese calendar of three hundred and sixty-six days, based on the movements of the Sun and Moon, which could date back to 3000 BCE.
By the second century CE, Chinese astronomers had noticed that their calendar was slowly becoming less and less reliable. The problem was due to a phenomenon called precession, which is a change in the orientation of the axis of rotation of a spinning body - in this case, the Earth. If you have ever played with a gyroscope or a spinning top, you may have witnessed this effect. As the speed of rotation decreases due to frictional forces, the gyroscope or spinning top begins to "wobble" around its axis. The Earth's rotation also experiences a "wobble", which causes each end of its axis to move in a circle in relation to the stars. Although this circular movement occurs very slowly (one complete turn occurs approximately once every twenty-six thousand years), the position of the stars in the night sky will slowly change. The Chinese adjusted their calendar to take precession into account during the fifth century CE.
The calendar most widely used today is the Gregorian calendar, which is a de facto international standard. The origins of the Gregorian calendar stretch back to the early days of Rome. The original Roman calendar is believed to have been a lunar calendar, and may itself have been based on one of several Greek lunar calendars, although various ancient Roman texts attribute it to the mythical figure Romulus, who supposedly founded the city of Rome in 735 BCE. The calendar of Romulus covered a period of three hundred and four days, divided up into the ten months of Martius, Aprilis, Maius, Iunius, Quintilis, Sextilis, September, October, November and December. Four of these months had thirty-one days each, while the rest all had thirty days. There were also fifty-one winter days between the end of December and the beginning of Martius that were not assigned to any month.
In circa 713 BCE Numa Pompilius, the king of Rome (Rome was still a kingdom at the time), reformed the Roman calendar. Allegedly, because the Romans thought even numbers to be unlucky, he reduced the length of each of the six months having thirty days to twenty-nine days each. This left a total of fifty-seven days that were unassigned. Numa Pompilius created two new months at the start of the calendar - January, with twenty-nine days, and February, with twenty-eight days. This resulted in a year of three hundred and fifty-five days. The year was now divided up into twelve months, four of which had thirty-one days each, with the remainder having twenty-nine days each (except for February, which had twenty eight days).
You have probably already noticed that this Roman calendar was ten days shorter than the three hundred and sixty-five day calendar we are familiar with today, which is based on the solar year. In order to bring the Roman calendar back into line with the solar year, it was necessary to insert an intercalary month (or leap month, if you prefer) every two years. This appears to have been inserted into the calendar (during an intercalary year) towards the end of February. The duration of an intercalary month is believed to have been about twenty days or so, although the details in various historical accounts vary. In any event, things must have been somewhat less than satisfactory, because the Roman dictator Gaius Julius Caesar (100-44 BCE) reformed the calendar once more in 46 BCE.
The Julian calendar, as it became known, was based on the solar year, which was known to be approximately three hundred and sixty-five-and-a-quarter days long. To achieve this, Caesar added either one or two days to each of the existing twenty-nine day months. The new calendar had three hundred and sixty-five days in a normal year instead of three hundred and fifty-five, with an additional intercalary day (or leap day) being added to February (normally twenty eight days long) every fourth year. Three additional months were added to the year 46 BCE in order to bring the start of the Julian calendar into alignment with the seasons once more, and the Julian calendar itself subsequently began on the first of January, 45 BCE.
A solar (or tropical) year is based on the time between two vernal equinoxes. The word equinox comes from the Latin aequinoctium, which means time of equal days and nights. An equinox is a point in time at which the Sun crosses the plane of the equator, which means that day and night will be of approximately equal duration over most of the globe. This occurs twice a year, once around 20th March (the vernal equinox) and once around 23rd September (the autumnal equinox). The solar year (i.e. the time between two vernal equinoxes) is three hundred and sixty-five days, five hours, forty-eight minutes and forty-six seconds.
The Julian calendar was virtually identical to the calendar we use today. Nevertheless, it differed from the solar year by approximately eleven minutes, which meant that eventually it would inevitably have to undergo some further adjustment. In 1572, the Italian cleric Cardinal Ugo Boncompagni (1502-1585) was elected Pope Gregory XIII. He is best remembered for commissioning changes to the Julian calendar in order to bring it into line once more with the solar year. The result was the Gregorian calendar with which we are familiar, and which is now almost universally accepted. The changes were implemented in 1582, by which time the vernal equinox had shifted by about ten days.
The change took place at midnight, on 4th October 1582. The following day, which would have been Friday 5th October, instead became Friday 15th October 1582. Although most Catholic countries in Europe adopted the changes more or less immediately, some protestant states refused to accept the new calendar for well over a century, and many Eastern European states, including Russia, held out until the early twentieth century.
Just another day
What difference does a day make? Well, according to Dinah Washington, "Twenty-four little hours brought the sun and the flowers where there used to be rain". But what is twenty-four hours? A good question really, and one that is not as straightforward to answer as you might think. The length of a sidereal day is the time it takes for the Earth to make one complete rotation on its axis relative to a given star. In other words, the interval between the moment a star appears at a particular point in the sky, and the moment it next appears at that precise point. This is actually about four minutes less than twenty-four hours, which is the time taken for the sun to appear at the local meridian (i.e. directly overhead) on two consecutive occasions, and by which we measure our days. We call this time interval the apparent solar day.
If you think about this for long enough you will understand why. As the Earth rotates on its axis, it is also orbiting the Sun, making one complete orbit over a period of approximately three hundred and sixty-five days. That means that in the time it takes for the Earth to rotate once on its axis, the Sun's position in the sky will have shifted by about one degree. Effectively, therefore, the Earth has to rotate through approximately one extra degree in order to "catch up". If you divide twenty four hours by three hundred and sixty-five, you get just under four minutes, which is roughly the additional time needed for the sun to appear at the local meridian twice running.
Things are actually even more complicated, partly due to the fact that the Earth's orbit around the Sun is elliptical (as opposed to circular). This means that both its distance from the Sun and the speed at which it moves along its orbital path vary throughout the year. Furthermore, the Earth's axis is not perpendicular to the plane of its orbit. The result of these factors is that the length of the apparent solar day is not constant, but can vary by up to twenty-two seconds. Our twenty-four hour day is therefore based on a mean solar day. The mean solar day, as its name suggests, is the average length of the apparent solar day, taken over the whole year.
Hours and minutes
If you were to be asked the question "how many hours are there in a day?", then the obvious answer that springs to mind is "twenty-four" (although I can think of a few people, myself included, who might say "not enough"). However, a day has not always consisted of twenty-four hours, and the hour itself has not always been of fixed duration. The Egyptian civilisation is generally credited with being the first to divide the day into smaller time intervals, and the available evidence suggests that they divided the time between sunrise and sunset into twelve parts, which were measured using various forms of shadow clock (and later sundials), perhaps as early as 1500 BCE. The night was also divided into twelve parts, but in the absence of the Sun the passage of time is believed to have been marked using the position of various stars, and later through the use of water clocks.
In ancient times, both the Greeks and the Romans are known to have used a similar system, dividing the time between sunrise and sunset into twelve hourly intervals. Obviously, because the hours of daylight vary throughout the year, these hourly intervals (known as temporal hours) varied in length from one day to the next. The significance of the number twelve may have originated with the Babylonian sexagesimal number system (a number system with a base of sixty), because twelve is a factor of sixty. It could also be related to the fact that both Egyptian and Babylonian astronomers recognised twelve major constellations through which the sun appeared to pass over the course of a year, each separated from the next by a thirty degree angle. There is also a theory that the number twelve was important because the three joints on each of the four fingers of one hand (twelve joints in total) were often used for counting.
Whatever the truth of the matter, it seems clear that the division of both day and night into twelve distinct time intervals by ancient civilisations laid the foundations for the modern twenty-four hour day. The development of equal-length hours probably arose from the need for astronomers to be able to accurately record the movement of various celestial bodies across the night sky. The Greek astronomer, geographer and mathematician Hipparchus of Niceae (c.190-c.120 BCE) is credited with being the first person to propose the division of the day into twenty-four equal-length equinoctial hours, so called because they are based on the equal length of day and night at the equinox (as mentioned earlier, an equinox occurs twice yearly, and is a point during the year at which the plane of the Earth's equator crosses the centre of the sun).
Another Greek astronomer and mathematician, the Egyptian-born Claudius Ptolemy (c.100-c.170 CE), is thought to have been responsible for dividing the equinoctial hour into sixty minutes of equal length, again possibly inspired by the sexagesimal number system used by the Babylonians. Despite these developments, however, most people continued to use seasonally varying hours until as late as the fourteenth century CE, when the first mechanical clocks began to appear in Europe.
Greenwich Mean Time (GMT)
Greenwich Mean Time (GMT) is one of the earliest time standards to be widely used. The standard was adopted by British railway companies in 1847 as a means of harmonising their timetables. Prior to this date, local times varied throughout the United Kingdom, and there was no established standard outside of London. The Great Western Railway Company had already made the decision to standardise its timetables, based on London time, in 1840. It was probably inevitable that the other major railway companies would follow suit.
Greenwich Mean Time defines the day as a twenty-four hour period equal to one mean solar day, from which the duration of a second is derived accordingly. The length of a mean solar day used to be calculated based on telescopic observations made at the Royal Observatory in Greenwich, London. The observatory was commissioned in 1675 by Charles II, and its designated purpose was to improve the navigation of ships at sea through the creation of accurate astronomical data. Navigators could use this data to find their longitude from anywhere in the world, providing they had an accurate time-keeping device that enabled them to determine the current time in Greenwich. The accurate measurement of time thus became an essential part of the observatory's remit, and in 1852 the Royal Observatory began transmitting the time to railway offices around Britain using the telegraph network.
The longitude of a location is the angular distance in degrees between that location and some prime meridian (a meridian is an imaginary line that runs from pole to pole). It essentially tells you how far east or west you are from the prime meridian. The Greenwich meridian is the meridian that passes through the Greenwich observatory, and because the Royal Observatory at Greenwich had built a reputation for producing reliable navigational and timekeeping data, it eventually became the internationally accepted prime meridian for navigational purposes. The status of the Greenwich meridian was established officially in 1884, when delegates from twenty-five countries attended the International Meridian Conference in Washington DC. Largely on the basis that it was already the de facto prime meridian for most of the world's seafaring nations, the Greenwich meridian was chosen to be Longitude 0°, and the starting point for each new day, year and millennium.
In 1928, the International Astronomical Union adopted the term Universal Time (abbreviated to UT) to replace "Greenwich Mean Time" as the name of the international telescope-based system used to determine the length of mean solar day. The new name was chosen in order to better reflect the almost universal acceptance of the standard, although I suspect that even today the abbreviation GMT is more familiar to most people. Observations at the Greenwich observatory itself ceased in 1954, and it is today part of the National Maritime Museum. Nevertheless, the Greenwich meridian is still the prime meridian, and will probably remain so for the foreseeable future.
Modern time systems
Given that there are twenty four hours in every day, sixty minutes in every hour, and sixty seconds in every minute, then a relatively simple mathematical calculation will lead you to the result that there are eighty-six thousand, four hundred (86,400) seconds in a day. Observations made at the Greenwich observatory enabled astronomers to accurately record the length of the solar day, from which they derived the length of the mean solar day. Given also that the average length of the solar (or tropical) year has been calculated to be 365.2421891 days (as of 2010), the approximate number of seconds in an average tropical year (currently) can be calculated as follows:
Solar year = 365.2421891 × 86,400 = 31,556,925.13824 seconds
Up until 1952, the duration of a second was derived by dividing the mean solar day (as measured by the Greenwich observatory) by 86,400. This was seen as being somewhat unsatisfactory, however, due to irregular fluctuations in the length of a mean solar day. Furthermore, the rotation of the Earth is gradually slowing down (the length of one rotation is increasing by approximately two milliseconds per century) due to friction caused by tidal action. In 1952, therefore, the International Astronomical Union adopted something called the Ephemeris Time scale. This was a new time standard that defined the second as a fraction of a solar year (i.e. a fraction of the Earth's orbital period around the Sun) rather than as a fraction of a mean solar day. Until 1967, the length of a second was officially defined as follows:
| One second = | 1 | × Solar Year |
| 31,556,925.9747 |
You will no doubt have noticed that the denominator in this fraction does not quite match up with the number of seconds we calculated for the solar year. We were careful to state that the number of seconds in the solar year was only the current figure, based on the length of the solar year calculated in 2010. Are we implying, then, that this number is subject to change? Well, yes, actually, and therein lies a problem. The fraction used in the definition used up until 1967 reflects the number of seconds in the solar year as calculated in 1900. Unfortunately, this number is slowly decreasing. One effect of the Sun's gravitational field is that it causes the Earth's orbit around the Sun to slowly become smaller. This in turn reduces the length of the Earth's orbital period around the Sun (i.e. the solar year).
Clearly, any definition of the second based on either the rotational period of the Earth or the duration of its orbit around the Sun is going to change over time. The amount by which it changes may well be far too small to have any bearing on most human activities, but for scientists it represents a very real problem. Scientists will insist, quite rightly, that any meaningful definition of time must be based on a constant value. Time, after all, is used to define a number of other quantities, such as velocity.
A solution emerged in 1955, in the form of an experimental atomic clock developed at the National Physical Laboratory in London, although it would be several years until a time system based on this new technology would be adopted internationally. We will be discussing the atomic clock in more detail shortly. For now, suffice it to say that the device was capable of generating a constant-rate high-frequency signal that could be used to provide a method of timekeeping that was both more stable and more convenient than any method based on astronomical observations. In 1967, the SI definition of the second was re-written in terms of the frequency supplied by a caesium atomic clock. The official definition of a second is:
"The duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom."
This means that the electromagnetic radiation emitted by caesium 133 has a waveform with a constant frequency of 9,192,631,770 hertz (cycles per second). This number will never change, which means that, as a means of measuring the passage of time, it is far more reliable than the use of astronomical observations. The reference to the "ground state" means that the definition applies to a caesium atom in its lowest energy state, which occurs at a temperature of zero degrees Kelvin (-273.15 degrees Celsius - essentially, absolute zero).
In 1971, the name International Atomic Time (abbreviated to TAI from its French name of Temps Atomique International) was given to a time scale based on the new SI definition of the second. The time scale in question had actually been in operation since 1958, although it had been known by various different names. From the outset, it had been synchronised with Universal Time (essentially Greenwich Mean Time), but due to its far greater accuracy had been drifting steadily apart from Universal Time. Note that, to ensure its continued accuracy, TAI is not based on the output of a single device. Rather, it is the weighted average of more than four hundred atomic clocks that are operated by some fifty or so laboratories around the world under strictly controlled conditions.
TAI formed the basis for what was later to become known as Coordinated Universal Time, which was abbreviated to UTC. The abbreviation is a compromise based on the anglicised version of the name and its French counterpart (Temps Universel Coordonné). UTC has actually been around since 1960, when it was formalised by the International Radio Consultative Committee in its Recommendation 374, although the name was not universally adopted until 1972. Time signals for the system were broadcast by the US Naval Observatory, the Royal Greenwich Observatory and the UK National Physical Laboratory. The broadcasts were closely coordinated, with the frequency of the signals initially being synchronised with Universal Time (UT), which was probably why the system became known as Coordinated Universal Time.
UTC is based on the extremely accurate atomic clock, whereas UT is based on the length of the mean solar day. Since the latter is both unpredictable and gradually increasing in length, it was inevitable that UTC would slowly drift away from UT. Each time the difference between the two became significant (a difference of around twenty milliseconds) the UTC signal would be phase shifted to synchronise it once more with UT. UTC was thus kept (more or less) in step with UT, but as a consequence of the frequent corrections, drifted further and further away from TAI (the time system on which it was originally based). Between 1958 and 1960, some twenty-nine such adjustments were made.
Things were further complicated by the fact that, for Universal Time, the duration of the second itself is defined as a fraction of the solar year, whereas for both TAI and UTC it is based on the frequency of the signal generated by an atomic clock. In addition, the need to make numerous minor adjustments to UTC in order to keep it synchronised with UT was seen as being far from satisfactory - not least because the difference between UTC and TAI was not an integer number of seconds. The redefinition of the second in 1967 meant that the duration of a second would now be the same, regardless of whether the system being used was TAI, UT or UTC. This represented an opportunity to introduce some much needed changes.
By the end of 1971, the difference between TAI and UTC was 9.892242 seconds. An adjustment of 0.107758 seconds was made to UTC at midnight on the final day of 1971 which meant that January 1st 1972 00:00:00 UTC was January 1st 1972 00:00:10 TAI precisely. This had the effect of making the difference between UTC and TAI an integer number of seconds (exactly ten seconds, in fact). At the same time, the tick rate of UTC was synchronised with that of TAI, and it was confirmed that, in order to simplify matters, all future adjustments made to UTC to keep it in line with UT would consist of increments of exactly one second. These increments were to become known as leap seconds.
The first leap second was added to UTC on 30th June 1972. At the time of writing, the most recent addition of a leap second to UTC occurred on 30th June 2015, bringing the total number of leap seconds added to UTC since 1972 to twenty-six, and the total difference between UTC and TAI to thirty-six seconds. The rotation of the Earth is monitored by the International Earth Rotation and Reference Systems Service (IERS), who announce the addition of a leap second at least six months in advance (in fact, it is only possible to determine when a leap second will be required a few months in advance, due to the unpredictable nature of the Earth's rate of rotation). A leap second is added when necessary in order to maintain Coordinated Universal Time within 0.9 seconds of Universal Time.
Leap seconds are always added on either the last day of June or the last day of December, although there is a contingency to add a leap second on the last day of either March or September should the necessity arise in future. At the time of writing (December 2015), leap seconds are required at intervals of approximately nineteen months, but the frequency is expected to increase as the Earth's rotation continues to slow down. It is estimated, for example, that by the end of the twenty-first century, a leap second will need to be added at intervals of just over eight months. At some point during the twenty-second century, two leap seconds will be required in each year in order to keep UTC synchronised with UT.
For those interested, UTC is currently formally defined by the International Telecommunications Union Recommendation ITU-R TF.460-6 Standard-frequency and time-signal emissions. Since 1972, UTC has officially been calculated by subtracting the accumulated leap seconds from TAI. So far, all of the leap seconds added have been positive (i.e. a second has always been added to UTC to keep it within 0.9 seconds of UT), although the option of using a negative leap second exists in order to allow for the (somewhat remote) possibility of the Earth's rotation speeding up rather than slowing down.
Time zones
As the Earth spins on its axis, the sun will rise and set on different parts of the world at different times. For that reason and by international agreement, the world is divided into twenty-four time zones, each of which is fifteen degrees wide, and each of which differs from its immediate neighbours on either side by exactly one hour. This system, which became known as Standard Time, dates back to 1879, when it was proposed by the Scottish-born Canadian engineer and inventor Sir Sandford Fleming. Fleming reportedly proposed a single twenty-four hour time system to be used worldwide after missing a train in Ireland in 1876, allegedly due to the fact that the departure time published on the timetable was shown as p.m. instead of a.m.
At a meeting of the Royal Canadian Institute, held in 1879, it was decided that the new time system should be linked to the anti-meridian of Greenwich. This is the meridian running from pole to pole on the opposite side of the world from the Greenwich meridian, at a longitude of one hundred and eighty degrees (180°). The use of local time zones linked to Standard Time was suggested at the same meeting, but it would be nearly fifty years before there was any kind of international consensus on this issue. By 1929, however, many countries had accepted a system of time zones based on Universal Time (which is essentially synonymous with Greenwich Mean Time).
The local time at Greenwich was generally accepted to be the starting point for calculating local time elsewhere in the world, mainly due to the fact that the Greenwich meridian had already been widely accepted worldwide as the prime meridian for navigational purposes. There were twenty-four time zones, each covering fifteen degrees of longitude. The offset of the centre of each time zone from the prime meridian determined the time within that time zone - one hour for every fifteen degrees west of the prime meridian. All clocks within the time zone would be set to the same "local time", but would be one hour behind those in the neighbouring time zone to the East, and one hour ahead of those in the neighbouring time zone to the West.
Today, most time zones are computed as an offset from UTC or GMT (also referred to as Universal Time or Western European Time), although many countries also implement a system of daylight saving in which clocks are advanced by one hour during the summer months in order to increase the number of daylight hours available to the majority of people at the end of their working day. Central European Time, for example, is one hour ahead of UTC. Tokyo Time (Japan) is nine hours ahead of UTC. New York, on the other hand, is five hours behind UTC, while Los Angeles (on the opposite side of the United States) is eight hours behind UTC.
The westernmost time zone from the prime meridian has an offset of UTC minus twelve hours (UTC-12), whereas the easternmost time zone (theoretically, at least) has an offset of UTC plus twelve hours (UTC+12). A very small number of countries use an offset of up to UTC plus fourteen (UTC+14) for geographical reasons. The Republic of Kiribati, for example, is an island nation of just over one hundred thousand people located in the Pacific Ocean. The republic is made up of thirty-three atolls and reefs, plus one raised coral island (Banaba), dispersed over an area of some three and a half million square kilometres that straddles the antemeridian (the meridian one hundred and eighty degrees east or west of the prime meridian).
The antemeridian is essentially the International Date Line (IDL), except that the IDL deviates from the antimeridian at certain points in order to avoid crossing certain territorial boundaries. As of 1995, Kiribati now extends over three time zones - namely UTC+12, UTC+13 and UTC+14. This somewhat strange-sounding arrangement makes sense once you realise that it was necessary in order to allow the various islands making up the republic to all be on the same day (at least for twenty-two hours out of twenty-four). Prior to 1995, the Line Islands, which form part of the Republic of Kiribati, were officially in time zone UTC-10, and were therefore never on the same day as the rest of the republic.
Note that the time zones adopted and administered by individual countries are primarily a matter for the countries concerned, and are not mandated by any kind of international law. A time zone adopted by a particular country often crosses over the nominal boundaries that exist in accordance with strict fifteen-degree offsets from UTC. Countries covering a large geographical area, such as Australia, Brazil, Canada, China, Russia and the United States, extend across multiple UTC time zones. Some of these countries have adopted internal time zones to reflect this fact.
The United States, for example, uses nine standard time zones. From east to west, these are Atlantic Standard Time (AST), Eastern Standard Time (EST), Central Standard Time (CST), Mountain Standard Time (MST), Pacific Standard Time (PST), Alaskan Standard Time (AKST), Hawaii-Aleutian Standard Time (HST), Samoa Standard Time (UTC-11) and Chamorro Standard Time (UTC+10). The boundaries of these standard time zones are not straight lines. Instead, they tend to follow state or county boundaries. China, on the other hand, uses a single time zone internally, despite spanning five UTC time zones. The official national standard time in China is known as Beijing Time internally, and China Standard Time (CST) internationally.
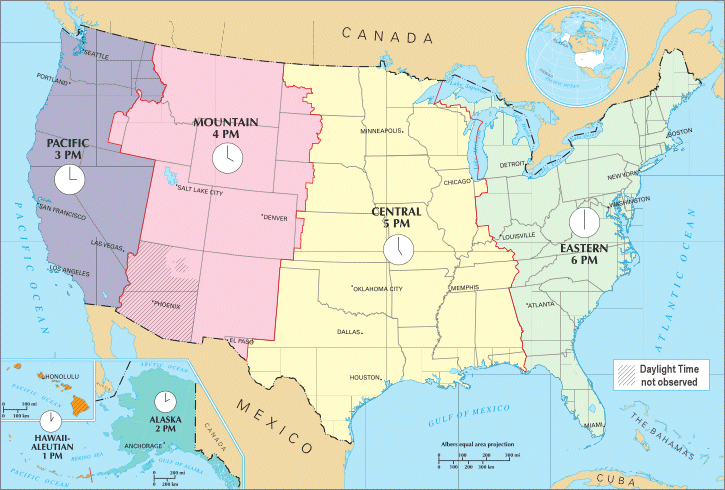
Time zones in the Continental United States do not have straight boundaries
Clocks before clockwork
Before the advent of clocks, man would mark the daylight hours by looking at the position of the Sun in the sky. At night, familiar patterns among the stars served a similar purpose. In order to measure time more precisely, however, man has had to invent various types of clock. The primary purpose of a clock is to measure the passage of time. All clocks rely on some physical process that occurs at a constant rate, and all clocks have some way of displaying information about the passing of time to an observer. Clocks are generally classified according to the methods they use to measure time, and the way in which the time is displayed. There is also a general dichotomy between clocks that indicate the time of day, and those that simply indicate how much time has elapsed.
Of the latter variety, candle clocks were perhaps among the earliest. Candle clocks were used in China from the sixth century CE, and have been used since that time in many other parts of the world. In its most basic form, the candle clock is a candle of uniform thickness, with markings at regular intervals along its length. Since the candle burns at a constant rate, the length of time required for the candle to burn down to each mark will be the same. The time period represented by each interval depends on the height of the interval, the diameter of the candle, and the kind of wax used by the candle-maker. The main disadvantage of the candle clock is that the rate at which a candle burns can vary with the quality of the candle used, and can also be affected by draughts.
Other methods of time measurement that are based on the rate at which something burns include the oil-lamp clock and the incense clock. The oil lamp clock typically has a glass reservoir for the oil marked with graduations so that the user can see how much oil has been consumed, and thus determine how much time has elapsed. The incense clock is essentially an incense stick marked with evenly spaced graduations. Like the candle clock, the incense stick burns at a steady rate, so the length of time required for it to burn down to each mark will be the same.
Shadow clocks and sundials
The earliest instruments used to tell the time of day are probably those that rely on the casting of shadows. Indeed, a number of ancient civilisations, including those of Babylon, China, Egypt, India and Mesopotamia, used a device called a shadow clock. In its most basic form, the device was simply a stick, placed upright and driven into the ground. The shadow cast by the stick during the daylight hours could be used to determine both the direction and elevation of the sun in the sky. The Egyptians built a number of obelisks (or tekhenu) which symbolised the Sun god Ra. These tall stone monuments, some thought to have been constructed as long ago as 3500 BCE, appear to have served as public shadow clocks, with markers placed around the base of the obelisk to indicate different times.
A more sophisticated version of the shadow clock consisted of an elongated oblong base marked at intervals along its length. At one end of the base is a raised crossbar. In the morning, the device is placed so that one end points east and the other west, with the crossbar at the eastern end so that it casts a shadow over the base. As the Sun rises, the shadow gets closer and closer to the crossbar. The base of the shadow clock typically had four marks. In the morning, the shadow cast by the crossbar would reach the mark farthest from the crossbar two hours after sunrise, and each subsequent mark at intervals of one hour. At noon, when the sun is directly overhead, the shadow disappears. The direction of the device is then reversed so that the crossbar is at the western end. As the sun sinks towards the horizon, the shadow moves further and further away from the crossbar. The last mark is crossed two hours before sundown.

Sketch showing a reproduction of an Egyptian shadow clock
The shadow clock was the forerunner of the sundial. The sundial is thought to have been used in Egypt as early as 1500 BCE. A sundial typically consists of a flat plate marked with lines radiating out from a central point and covering a roughly semi-circular area. A perpendicular arm called a gnomon is mounted on the plate, and casts a shadow over the plate when the Sun shines on it. As the Sun moves across the sky from east to west, both the direction and length of the shadow will change. The lines marked on the plate are usually arranged to represent the daytime hours from six a.m. to six p.m. If the lines have been correctly calibrated, and providing the gnomon is aligned with the Earth's axis of rotation, the shadow cast by the gnomon should always indicate the correct time during the daylight hours, regardless of the time of year (unless the sun is obscured due to adverse weather conditions).

An ornamental sundial in Perth, Australia
The merkhet
Obviously, shadow clocks and sundials were limited in the sense that they were only useful during the daylight hours. During the hours of darkness, the Egyptians (and other ancient peoples) had to rely on other methods of timekeeping such as candle clocks, oil lamp clocks, or water clocks (see below). From at least 600 BCE, the Egyptians are known to have used an instrument called a merkhet (which means "instrument of knowing") to determine the time at night. This essentially consisted of a rod, usually carved from wood or bone, with a plumb-line attached to it to enable the user to establish a true vertical line. It is thought that two merkhets were used in tandem, together with a pair of sighting rods (or bays), each consisting of a vertical rod with a slit in one end, in order to establish a line of sight with Polaris (also known as the North Star or Pole Star), as shown by the illustration below.

Merkhets being used to establish a north-south meridian (image credit: Dave Shapiro)
Polaris lies almost in direct line with the Earth's axis of rotation, and thus remains almost motionless in the night sky. It currently lies about three quarters of a degree away from the Earth's axis of rotation, and therefore rotates around the axis in a small circle approximately one-and-a-half degrees in diameter. Polaris is thus precisely aligned with true north twice a day, and will never deviate by more than three quarters of a degree east or west of true north. For the Egyptians, establishing a line of sight with Polaris was a simple but effective method of creating a north-south meridian. The time at which a particular star crossed the meridian could be determined using a water clock, and recorded. As a consequence, it became possible to keep track of the time at night by observing the transit of particular stars across the north-south meridian.
Water clocks
Water clocks have a long history. Evidence has been found to suggest that they were used in Egypt at least as long ago as 1500 BCE. One very simple type of water clock employed an empty bowl with a small hole in its base. This bowl would be placed into a larger bowl that was full of water. The smaller bowl would gradually fill with water and sink to the bottom of the larger bowl. The amount of time required for the smaller bowl to sink would have been measured, probably using a sundial or shadow clock, and was thus known. Once the smaller bowl started sinking, it would immediately be emptied and placed once more in the larger bowl. The passage of time would typically be recorded by placing a small stone into a jar each time the smaller bowl sank. Water clocks of this type were still in use in some parts of North Africa well into the twentieth century.
Another kind of water clock consisted of a stone vessel with a small hole near the bottom. The vessel was filled with water, which then dripped from the hole. The amount of time taken for the vessel to become completely empty would depend on the capacity of the vessel and the size of the hole. Marks on the inside of the vessel were used to indicate how much time had elapsed. One obvious advantage of this type of clock is that it could be used at night, unlike shadow clocks or sundials. It was also more reliable than a candle or lamp clock. One problem, however, was that the water pressure inside the stone vessel would fall as the volume of water decreased, which caused the flow of water to slow.

An ancient Egyptian water clock (picture credit: Ian Corey)
There is evidence to suggest that water clocks of one kind or another were used by a number of ancient civilisations, including those of Greece, Rome, and China. The ancient Greeks, for example, are known to have used water clocks since at least the fourth century BCE (the Greek name for the water clock was clepsydra, which means water thief). Even so, the basic design of the water clock does not appear to have changed much until about 100 BCE. Around this time, the design of water clocks used by both the Greeks and the Romans appears to have evolved in order to solve the problem of falling water pressure. A conical vessel was now used, with the wider end facing upwards. As the water pressure dropped, less water flowed out of the vessel in a given time interval, but the height of the water (which is what was used, remember, to mark the passage of time) decreased at an even rate.
Greek, Roman, and later Chinese horologists (a horologist is someone who makes clocks) began to produce more and more sophisticated designs, although many of the additional features were more cosmetic than functional in nature. Water clocks were often adorned with intricate carvings, or drove complex mechanisms designed to produce a series of chimes or to animate miniature figures of people or animals. One remarkable example is the so-called "Tower of the Winds" in Athens, reportedly built by the Macedonian astronomer Andronicus of Cyrrhus in about 50 BCE, which still stands today. It is essentially a twelve-metre tall octagonal stone clock tower that combines a water clock with eight sundials and a wind vane. The water clock is driven by water flowing down to the tower from the Acropolis (an ancient citadel located on a rocky outcrop above Athens).

The Tower of the Winds in Athens (picture credit: Alun Salt)
The hourglass
An hourglass (or sand clock) consists of two glass bulbs, connected by a narrow neck. When in use, the hourglass is oriented so that one of the bulbs is positioned directly above the other. The hourglass contains a quantity of dry sand, or some other fine-grained material. Any sand in the upper bulb will flow through the neck to the lower bulb under the influence of gravity. Assuming that all of the sand is initially in the upper bulb, and depending on the amount of sand present, the coarseness of the sand, and the diameter of the neck at its narrowest point, the sand will take a specific amount of time to trickle through the neck and into the lower bulb.
If the hourglass is then inverted so that the upper bulb becomes the lower bulb, and the lower bulb (the one with the sand in it) becomes the upper bulb, the sand will take the same amount of time to trickle back into the lower bulb. Every time the upper bulb is empty, the hourglass can be inverted once more, and the sand will again trickle from the upper bulb to the lower bulb. This process will always take exactly the same amount of time.
If you think about it, the hourglass is in some ways a perfect timekeeping solution. It is completely re-usable; unlike candle clocks or oil-burning clocks, no materials are actually consumed while it is in use. It also works just as well at night as it does during the day, unlike shadow clocks or sundials, and it does not rely on something that can freeze or evaporate, unlike water clocks. Hourglasses are also cheap and relatively easy to manufacture. In fact, thanks to the fact that it could function perfectly well on the deck of a moving ship, the hourglass was used by sailors for general timekeeping and navigation purposes from the beginning of the fourteenth century up until John Harrison developed the first accurate marine chronometer in 1735.
The Portuguese explorer Ferdinand Magellan (1480-1521) led an expedition to the East Indies that lasted from 1519 to 1522, and resulted in the first recorded circumnavigation of the globe. Unfortunately Magellan himself did not survive the trip (only one of the five ships that set out actually made it home), but he was known to have used eighteen hourglasses on each ship.
There is some speculation that hourglasses were used at sea much earlier, perhaps as early as the eleventh century CE. Glass blowing technology certainly existed in Europe at that time. Glassblowing workshops had been set up in Rome during the first century CE, probably employing artisans gathered from the easternmost reaches of the Roman Empire, including the territories today known as Lebanon, Israel and Cyprus. Glassblowing centres were later established in several Italian provinces.
The history of the hourglass itself is not known with any certainty. There is little evidence of it having been in widespread use in Europe before the fourteenth century. Some sources claim it was invented in Egypt around 150 BCE, and there is certainly evidence to suggest that hourglasses were in use in Egypt during the fourth century CE. According to other sources, hourglasses may have been used by the Greeks as early as the third century BCE (the Greek name for the hourglass is clepsammia).
Hourglasses were obviously not particularly suited to keeping track of the time of day. They were however very useful for measuring specific periods of time - the duration of a church sermon or a university lecture, for example. As mechanical clocks became smaller, more accurate, and more affordable, the hourglass gradually became less and less significant as a timekeeping device. It didn't disappear altogether, however. Even today, you can buy an hourglass egg-timer very similar to one that might have been used several centuries ago. You can even purchase decorative hourglasses to adorn your home.

An hourglass in a wooden frame, possibly used as an egg timer
Even if it is no longer widely used, the hourglass is still very much a part of our cultural heritage. You have almost certainly seen an hourglass symbol on your computer desktop, telling you that some process or other is ongoing and requires a certain amount of time to complete. It seems likely that the reason why the hourglass symbol has outlived the usefulness of the hourglass as a timekeeping instrument is because of its unique and instantly recognisable shape.
Early mechanical clocks
Although most of the clocks developed during the first millennium and the early part of the second millennium BCE still relied on the flow of water to power them, many of the more advanced examples could also be considered to be "mechanical" clocks simply because they used various types of mechanism to display the time. Gradually, however, the design of such clocks was modified to allow the use large weights to drive the various clock mechanisms instead of a flow of water. The weight would typically be attached to a chord wrapped around a spindle. As the weight moved downwards under the influence of gravity, the chord would unwind and force the spindle to turn, driving the clock mechanism.
There are two significant challenges when using a weight to power a clock. The first challenge is to ensure that the chord unwinds at a constant rate, so that the clock can mark the passage of time in equal increments. The second is to restrict the speed at which the chord unwinds, since the chord, with the weight attached to it, must be rewound on the spindle each time it becomes fully extended. Both of these challenges could be met using a mechanism called an escapement. This is a general term for any mechanism that transfers energy to the time-keeping element of the clock at a constant rate in the form of a series of "impulse actions" or "oscillations".
Escapement mechanisms had already been developed for water-driven clocks. The most basic of these mechanisms typically involved a container located at one end of a beam mounted on a central spindle (sometimes referred to as the barrel). Water was allowed to flow into the container at a constant rate. A counterweight attached to the other end of the beam ensured that the container remained in an upright position until it was full of water. Once full, the weight of the container would exceed that of the counterweight and the beam would rotate on its axis, allowing the container to discharge its contents. Once empty, the container was returned to its upright position by the counterweight, and the process would begin again. Each cycle would advance the clock's mechanism by a fixed amount.
The earliest form of escapement used for mechanical clocks driven by weights was probably the verge and folio escapement, which appeared in Europe some time during the thirteenth century CE. This mechanism is thought to have evolved from similar mechanisms used in bell-ringing apparatus. The toothed wheel you can see in the illustration below is called the escape wheel (or crown wheel, due to its appearance). The escape wheel is driven by a weight (not shown), which is attached to a chord wound around the barrel of the crown wheel. A vertical rod called the verge is located in close proximity to the escape wheel, and perpendicular to the axis of the escape wheel. The verge has two protruding flanges (called pallets) angled at about ninety degrees to one another so that, when one pallet is engaged with the escape wheel's teeth, the other is not.
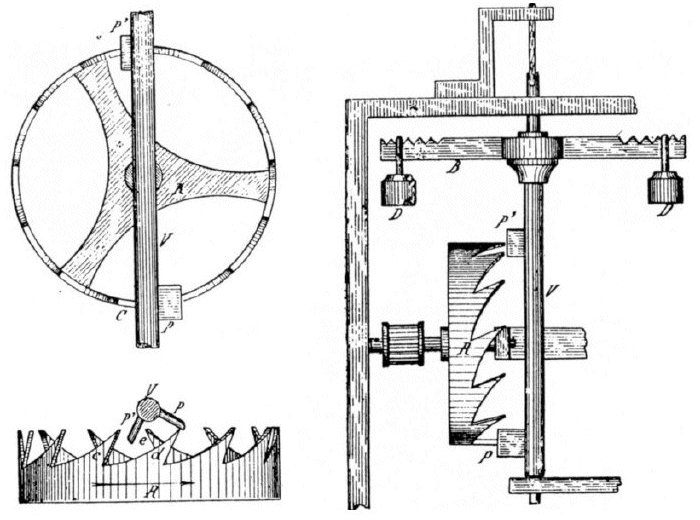
Sketch of a basic verge and foliot mechanism (origin unknown)
As the escape wheel turns, it pushes the pallet with which it is currently engaged (for argument's sake we'll assume this is the pallet at the top end of the verge), which turns the verge in one direction. As the verge turns, the pallet that is currently engaged with the escape wheel will move clear of the teeth, while the other pallet (the one at the bottom end of the verge) is rotated into position so that it can engage with the teeth. When the escape wheel engages with this second pallet, it will push it in the opposite direction. The verge is thus rotated first one way, and then the other. The action of the escape wheel engaging, first with one pallet and then the other, is where many old mechanical clocks get their characteristic "tick-tock" sound.
The foliot is the horizontal beam mounted on top of the verge. You can see in the illustration that it has weights suspended from both ends, the purpose of which is to inhibit the speed at which the verge can rotate (by increasing the overall inertia of the verge and foliot assembly), thus regulating the speed of the clock mechanism. The notches cut into the top of the foliot allow the position of the weights to be adjusted, either to slow the clock down (by moving the weights towards the ends of the foliot) or to speed the clock up (by moving the weights towards the centre of the foliot).
The verge and foliot mechanism was, in one form or another, in widespread use for several centuries after it first appeared. The accuracy and reliability of clocks employing this kind of mechanism, however, was limited. To some extent, of course, performance depended on the workmanship of the clockmaker and the degree to which the clock itself was maintained, but it could also be affected by factors such as friction, and the inevitable wear and tear caused by the constant interaction between the escape wheel and the verge.
Another problem was that the momentum of the foliot often caused it to push the escape wheel backwards for a short distance before the force of the weight acting on the escape wheel was able to reverse the direction of the verge's rotation - a phenomenon known as recoil - which adversely affected the accuracy of the timekeeping mechanism, and at the same time increased the wear on both the escape wheel teeth and pallets. In time, the foliot was replaced by a weighted balance wheel that performed much the same function, although the improvement in performance achieved was probably marginal.
Spring-driven clocks
Clocks driven by springs (as opposed to weights) began to appear during the early part of the sixteenth century CE. Using a spring to power a clock mechanism as opposed to heavy drive weights allowed clocks to be made considerably smaller. So much so, in fact, that it eventually became possible to make portable timepieces that were small enough to be carried in a pocket or worn about the person. The invention of the watch is usually accredited to the German locksmith and clockmaker Peter Henlein of Nuremberg (1485-1542). He made a number of small, highly ornate, and very expensive spring-powered timepieces that were popular among the nobility of the time.
These early spring-driven timepieces derived their power from a spiral spring called the mainspring that had to be wound periodically by the owner. They were not really small enough to be classed as watches or even pocket-watches by any modern definition, and didn't even keep particularly good time, since they ran slower and slower as the spring unwound. They were undoubtedly viewed as fashion accessories by their owners. Their price, unusual design, and uniqueness meant that they were often acquired more as status symbols than for their time-keeping properties.
Even though the balance wheel replaced the foliot in spring-driven timepieces, the speed at which the verge mechanism operated was still almost entirely dependent upon the force supplied by the spring, which of course decreased steadily as the spring wound down. The problem was partially solved by the invention of a mechanism called a stackfreed towards the end of the sixteenth century. In essence, this is a simple cam assembly, the purpose of which is to even out the force of the mainspring. The cam, which is eccentric, is mounted on a gearwheel (or stopwheel) linked to the mainspring arbor (the spindle around which the mainspring is wound) via a smaller gearwheel. The gear ratio is such that the cam makes one complete turn as the spring winds down.
A stiff spring arm (the follower arm) is mounted inside the timepiece as shown in the illustration below. At the end of the spring arm is a small roller (the follower) which rests on the edge of the cam. The follower exerts a force on the cam, slowing the unwinding of the mainspring and thereby reducing the power supplied by the mainspring to the verge. The shape of the cam is such that, as it turns, the force exerted on it by the follower is reduced. This allows the mainspring to unwind more quickly, so that it supplies more of its dwindling stored energy to the verge. The idea is to keep the power supplied to the verge by the mainspring constant by gradually increasing the rate at which it unwinds.
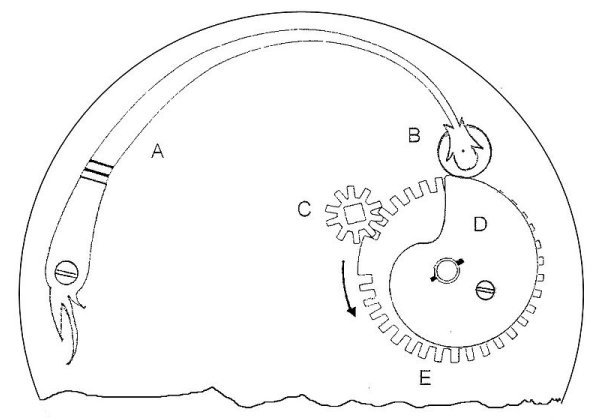
Drawing of a stackfreed assembly, showing the follower arm (A), follower (B), mainspring arbor (C), cam (D) and stopwheel (E)
Notice that there is a small section of the stop wheel in which there are no teeth. In one direction, this has the effect of preventing the mainspring from being wound too tightly, which could damage it. In the other direction, it prevents the mainspring from unwinding completely. The mainspring is thus never either completely wound or completely unwound, which helps to even out the amount of power it supplies to the verge at any given time. The cutaway section you can see on the cam in the illustration allows the force applied to the cam by the follower to fall rapidly as the power in the mainspring dissipates, resulting in a greater proportion of whatever power remains in the mainspring being transferred to the verge.
As you may have surmised, using the frictional force applied by one spring to regulate the power provided by another spring, although ingenious, did not prove to be particularly efficient. A more effective mechanism for smoothing out the power supplied by the mainspring emerged in the shape of the fusee. Although the origins of the fusee are not known in any detail, it is thought that the inspiration for this device came from the winding mechanisms used on some mediaeval crossbows. The fusee is a grooved and (more or less) cone-shaped pulley, attached to which is a chain (early versions used a chord made of gut or wire, but these had a tendency to break). The other end of the chain is attached to the mainspring barrel, as shown in the illustration below.

A woodcut engraving showing a mainspring and fusee in wound and unwound states. The components identified here include the mainspring arbor (A), the mainspring barrel (B), the chain (C), the fusee (F) and the winding arbor (G).
A helical groove ran around the fusee's cone from top to bottom, designed to accommodate the chain. Early versions of the fusee tended to be elongated and narrow, which made the timepieces in which they were used considerably bulkier than if a stackfreed mechanism had been used. In later examples, the height was significantly reduced at the cost of an increase in diameter.
The spiral mainspring is wound around a stationary spindle (the mainspring arbor) inside a cylindrical enclosure (the mainspring barrel). As the spring unwinds, it turns the barrel (to which one end of it is attached), which turns the fusee by pulling on the chain. The large gear wheel on the bottom of the fusee drives the clock's time keeping mechanism. The spring is wound up using the winding arbor, which protrudes from the base of the fusee. As winding takes place, the chain is wound around the fusee from the bottom to the top.
When the force supplied by the spring is at its strongest, it acts on the fusee at the point where its diameter is smallest. As a result, the angle through which the fusee turns in proportion to the force applied is relatively small. As the spring winds down, the chain gradually unwinds from the top to the bottom of the fusee. Thus, while the force of the mainspring is slowly decreasing as the spring unwinds, the diameter on which that force is acting is actually increasing, providing a greater turning moment (we will be covering the topic of turning moments in another section). As a consequence, the angle through which the fusee turns in proportion to the force applied remains constant. The force required to wind the mainspring also remains constant as the spring is being wound.
Although the fusee was a far more efficient way of regulating the power supplied by the mainspring than the stackfreed, it had its disadvantages. Even though fusees became more compact over time, they still took up far more space than a stackfreed, resulting in timepieces that were significantly larger. The fusee also cost more to make, and due to its relative complexity was more difficult to maintain and repair. What was needed was some kind of harmonic oscillator that would run at a constant rate, regardless of variations in the force supplied by the mainspring, and that did not involve a bulky and expensive mechanism. A pendulum could be used as the harmonic oscillator in large timepieces, but it was obviously not an option for smaller clocks and watches.
The crucial development was the invention of the balance spring. The credit for this invention is disputed, although it seems likely that the idea originated with the English scientist Robert Hooke (1635-1703). It was the Dutch mathematician and scientist Christian Huygens (1629-1695), however, who constructed the first functional timepiece to use it, in 1675. The balance spring is typically a fine spiral or helical spring that obeys Hooke's Law. This law essentially states that the force required to compress or extend a spring by some distance is proportional to that distance. In the case of a spiral or helical spring, the force is proportional to the angular distance through which the spring is turned.
The balance wheel is connected to the balance spring in such a way that, when the balance wheel is turned in one direction by the power provided by the mainspring, it partially winds the balance spring. This induces torque (the tendency of a force to rotate an object about some axis) in the balance spring, which stops the balance wheel from turning in one direction and pushes it back in the opposite direction. The balance wheel (which is weighted) will continue turning beyond its rest position because of its inertia. Torque will again develop in the balance spring, which now acts to push the balance wheel back in the other direction.
The balance wheel will therefore oscillate back and forth. Because of the relationship between the force applied by the balance wheel on the spring and the angle through which the spring is turned by that force (as defined by Hooke's Law), the balance wheel will be isochronous - i.e. it will oscillate back and forth at the same frequency, regardless of the amplitude of the oscillations. The balance spring and the balance wheel together thus become the harmonic oscillator we are seeking. In order for the balance wheel to continue to oscillate, however, it will need to get a nudge every so often from the mainspring. The job of the escapement is to ensure that this happens at exactly the right time. The diagram below shows a lever escapement of the kind invented by the English watch and clockmaker Thomas Mudge (1715-1794) in 1750.
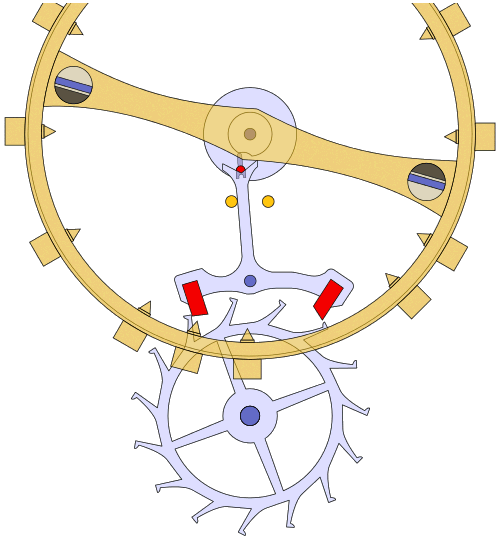
A lever escapement is used to regulate the power supplied to the balance wheel (image: Fred the Oyster)
In the animation below, the escape wheel (driven by the mainspring) is turning in a clockwise direction. One of the teeth on the escape wheel pushes against the pallet attached to the right-hand branch of the lever, forcing it upwards and causing the lever to rotate to the left. As it does so, the fork at the top of the lever will engage with an impulse pin (not shown) mounted on the central part of the balance wheel, giving it a momentary push. At the same time, the pallet attached to the left hand branch of the lever moves downwards, engaging with one of the teeth on the escape wheel and preventing it from turning any further.
Animation showing the action of a lever escapement (creator: Mario Frasca)
When the torque in the balance spring pushes the balance wheel back in the opposite direction, the impulse pin engages once more with the lever, turning it to the right. This releases the escape wheel, and the cycle is repeated. In a modern spring-powered watch, this action typically occurs four times per second. During each cycle, the escapement gives the balance wheel a short push to keep it oscillating about its rest position. The rate of the oscillation can be adjusted in some watches using a small lever which is attached to one end of the balance spring, allowing the effective length of the balance spring to be altered.
The introduction of the balance spring greatly improved the accuracy of portable timepieces to the extent that they were accurate to within ten minutes per day (prior to this innovation, the degree of inaccuracy was measured in hours per day rather than minutes). Over time, there were further improvements, both in the design of spring-driven clocks and watches, and in the quality of the materials used in their construction. It was finally possible to make timepieces that were both reasonably accurate (to the extent that many now included a minute hand) and small enough to truly be classed as pocket watches.
The marine chronometer deserves a special mention here, both because of its importance in the field of navigation and because it solved a number of problems associated with conditions at sea. Accurate time keeping was of vital importance to navigators. By the eighteenth century, a navigator could calculate their latitude with a high degree of accuracy, thanks to charts and almanacs compiled by astronomers at the Greenwich Royal Observatory. In order to do so, however, they had to know the time in Greenwich with a good degree of accuracy.
Clocks with pendulums, although sufficiently accurate on land, were virtually useless on a rolling ship. By 1761, more than two decades after producing his first chronometer, the English carpenter and self-taught clockmaker John Harrison (1693-1776) had built a spring-driven chronometer that some sources have described as resembling an "oversized pocket watch". This timepiece used a unique spring and balance wheel escapement, and the materials used for its construction were carefully chosen to compensate for the effects of both friction and variations in temperature. The final version of Harrison's marine chronometer was accurate to within about one fifth of a second per day, and allowed longitude to be determined to within half a degree.
Pendulum clocks
Another major advance in clock technology came with the introduction of the pendulum. Although the Italian astronomer, physicist, engineer, philosopher, and mathematician Galileo Galilei (1564-1642) is thought to have designed a clock mechanism involving a pendulum early in the seventeenth century CE, although there is no evidence to suggest that he ever built one. Instead, the invention of the pendulum clock is usually accredited to Christiaan Huygens (see above), who came up with the mathematical formula relating the period of oscillation of a pendulum to its length.
Huygens determined that, at least for relatively small oscillations (i.e. how far the pendulum swings back and forth), a pendulum with a length of ninety-nine-point three-eight (99.38) centimetres would have a period (i.e. the time required for a swinging pendulum to achieve one complete cycle) of two seconds. In other words, once set in motion, a pendulum of this length would be at the bottom of its swing (i.e. at its rest position) at intervals exactly one second apart. Huygens had the first pendulum-driven clock built in the Hague in 1657.
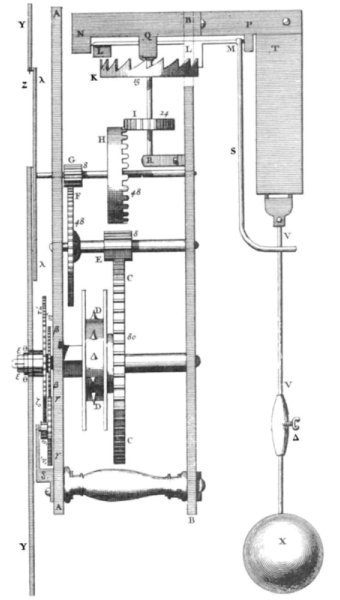
A drawing of Huygens' pendulum clock, from his treatise Horologium Oscillatorium (1673)
The verge escapement was still used, but now the verge itself, while still perpendicular to the barrel of the escape wheel, was mounted horizontally rather than vertically. The pendulum essentially replaced the foliot or balance wheel. Huygens' clock was accurate to within one minute per day. The English clockmaker William Clement was sufficiently interested in this development that in (circa) 1670 he built the first longcase clock (or grandfather clock, as it is better known today). The name comes from the fact that a long case (usually made of wood) is required to house the pendulum, and to provide a long drop space for the weights that power the clock.
It should perhaps be noted here that clocks can also have short pendulums. However, long pendulums require less power to keep them in motion, are subject to smaller frictional forces, suffer less wear, and are generally more accurate than their shorter counterparts. We should also mention that a change in the amplitude of the swing does affect the period of the pendulum very slightly. If the amplitude changes from four degrees (4°) to three degrees (3°), for example, the period of the pendulum would decrease by approximately 0.013 percent. This translates to a gain of about twelve seconds per day.
The problem can be eliminated if the pendulum has a cycloidal path (as opposed to a circular arc), but this precludes the use of a rigid pendulum. The alternative is to keep the amplitude of the swing as small as possible, so that its movement is as close to linear as possible. Clement knew that the pendulum needed to be given a "push" to keep it swinging at the same amplitude, and that this "push" should occur as close as possible to the mid-point of the pendulum's swing in order to provide energy to the pendulum whilst minimising the escapement error (i.e. the degree to which the escapement interferes with the motion of the pendulum). The verge escapement used by Huygens did the job, but the anchor escapement developed by Clement was a significant improvement.

Animation showing the action of an anchor escapement (creator: Chetvorno)
As you can probably see from studying the animation, the anchor escapement (so-called because the top end of the pendulum somewhat resembles an anchor) is very similar in operation to the lever escapement used in many spring driven watches. As one of the escape wheel's teeth pushes one arm of the pendulum up and to the right, another of its teeth is engaged by the pendulum's other arm as it moves down and to the right, temporarily preventing the escape wheel from turning. As the pendulum swings back to the left, the escape wheel is released, allowing it to give the pendulum a further push to the right as the cycle is repeated.
Clement's longcase clocks were accurate to about ten seconds per day, but further refinements over the next few decades would improve accuracy even further. For example, a pendulum made of metal will change in length to some extent as it expands or contracts with changing temperatures, which in turn changes the period of the pendulum slightly. Over time, special alloys were developed for pendulums in order to minimise the effects of thermal expansion and contraction.
Electric clocks
The first electric clock was patented by the Scottish clock and instrument maker Alexander Bain (1810-1877) in 1840. It would probably be more accurate to describe such clocks as electro-mechanical clocks, since electricity is used to provide power to an otherwise fairly conventional clock mechanism, and plays no direct role in timekeeping. Bain's clock featured an electromagnetic pendulum. An electric current is used to maintain the pendulum's motion, rather than weights. In other types of electric clock, an electric motor is used to periodically wind a mainspring or raise the drive weights.
Electricity plays a somewhat more direct role in timekeeping in clocks that are powered by an alternating current (AC) mains supply. These clocks do not have their own oscillator; there is no pendulum or balance wheel involved. There are various versions of this kind of clock. A digital version might count the cycles of the alternating AC waveform, which is generated at a precise frequency of fifty cycles per second by the electricity supply company. The clock will advance by one second each time it reaches a count of fifty, and then start counting again.
An analogue version typically drives a synchronous electric motor, in which the rotation of the motor's drive shaft is synchronised with the frequency of the supply current. The hands of the clock are driven by the rotating shaft using appropriate gearing to allow the hour, minute, and second hands to be turned at the correct speed.
Electronic (quartz) clocks
Up until the early part of the twentieth century, pendulum clocks were still the most accurate clocks. In fact, the electro-mechanical Shortt-Synchronome free pendulum clock, invented in 1921 by the British railway engineer William Hamilton Shortt and British horologist Frank Hope-Jones, was probably the most accurate pendulum clock ever produced. It was accurate to within one second per year, and was used in observatories and laboratories worldwide. From the late 1920s until the early 1940s, these clocks were used for maintaining national time standards in a number of countries, including the US and Britain.
The successor to the pendulum clock was already in development, however, in the shape of the quartz clock. Quartz is a crystalline form of the chemical compound silicon dioxide, and one of the most commonly occurring minerals on our planet. The piezoelectric properties of quartz crystals were first discovered by the French physicists Jacques Curie (1856-1941) and his younger brother Pierre Curie (1859-1906) in 1880. Being piezoelectric, quartz has the property that it produces a tiny electric current when it is deformed or put under pressure. Conversely, if an electric current is applied to a quartz crystal, it will change its shape.
In fact, when sufficient current is applied to a quartz crystal of just the right shape and size, it will vibrate at a constant frequency. The precise frequency at which the crystal vibrates will depend upon its dimensions and how it has been cut. In a quartz clock, a current is supplied to the crystal, causing it to vibrate at a known frequency. Electronic circuitry inside the clock counts the vibrations, and generates a pulse once every second. This pulse can then be used to control either a digital display, or a stepper motor that controls the movement of the hour, minute and second hands of the clock.
An oscillator controlled by a quartz crystal is many times more accurate than one that is controlled by a pendulum or a balance wheel. Although the operating frequency of a crystal may be affected very slightly by changes in temperature, the effect is negligible by comparison with the effect that a change in temperature would have on a pendulum or balance wheel in a mechanical clock. And, unlike the mechanical clock, a quartz clock is unaffected by variations in the Earth's gravitational field.
The first quartz clock was built in 1927 by Warren Marrison and J. W. Horton at the Bell Telephone Laboratories in Canada. The electronic counters used in these early clocks were built using valves (sometimes called vacuum tubes), because the miniaturisation that would become possible with the invention of the transistor and the integrated circuit was still decades away. As a consequence these clocks were large and very expensive, which pretty much limited their use to a laboratory setting. They were nevertheless far more accurate than any other kind of clock existing at the time, and were adopted by the National Bureau of Standards (now the National Institute of Standards and Technology) in 1929 to provide primary frequency and time standards for the US.

Quartz oscillators at the US Bureau of Standards
Quartz is an ideal material for use in electronic oscillator circuits. It is cheap, readily available, relatively easy to machine, and uses only tiny amounts of electricity (a quartz watch battery can sometimes last for years). The real breakthrough came with advances in electronics during the 1960s and 1970s that made it possible to produce miniaturised electronic components, and integrated circuits containing thousands of transistors. For the first time, it became possible to manufacture quartz clocks and watches for the consumer market.
The quartz crystal used in a modern quartz clock or watch is tiny. It typically consists of a crystal wafer that has been precision lapped or laser-trimmed, usually into a shape that looks a bit like a tuning fork. Two parallel surfaces on the crystal wafer have metal plates bonded to or deposited on them to enable the crystal to be connected to an electrical circuit. The crystal wafer is housed inside a small metal cylinder, which is what you would see if you could look into the inner workings of the clock or watch.
The crystal is typically designed to operate at a frequency of 32,768 (2 15) Hertz, for practical reasons. A crystal with a significantly lower frequency would be much larger, while one with a significantly higher frequency would require a significantly greater operating current. The choice of frequency (32,768 Hz) is also quite convenient, since it means that a 15-bit binary digital counter driven by the frequency will overflow at precise one-second intervals.
The first prototype quartz wristwatch was developed in 1967 by the Centre Electronique Horloger (CEH) in Switzerland, but it was the Japanese company Seiko who produced the world's first commercial quartz wristwatch - called the Astron - in 1969. The Astron initially retailed at a price of four-hundred and fifty thousand yen, which in those days was equivalent to about twelve hundred and fifty US dollars. For those interested in such things, an original 1969 Astron quartz wristwatch sold at auction in 2012 for nearly six thousand pounds sterling!

A look inside the Seiko Astron (Image: Deutsches Uhrenmuseum)
Modern quartz watches are much cheaper (and probably far more reliable, thanks to improvements in technology and manufacturing techniques). Indeed, quartz clocks and watches have dominated the marketplace since the 1980s because they offer excellent performance at a reasonable price. Quartz technology is now found inside countless household appliances and electronic devices - just about anything, in fact that requires a timing function, including personal computers, tablets and mobile phones.
Atomic clocks
As we have already learnt, current time standards such as Coordinated Universal Time (UTC) and International Atomic Time (TAI) are based on the SI definition of the second, which is derived using the frequency of the electromagnetic radiation emitted by caesium-133 in its ground state. International primary frequency and time standards are maintained using a number of atomic clocks operated in laboratories around the world. Notable examples include the caesium fountain clock operated by the National Physical Laboratory (NPL) in Teddington, London, which currently serves as the United Kingdom's primary frequency and time standard, and a similar clock called NIST-F1 operated by the National Institute of Standards and Technology in Boulder, Colorado, which provides the primary frequency and time standard for the United States.
An atomic clock uses the frequency of electronic transitions occurring in a particular kind of atom to measure time. The idea was first suggested by the Irish mathematician, physicist and engineer William Thompson (1824-1907), perhaps better known as Lord Kelvin, in 1879. At the time, however, there was no practical means of implementing his ideas. Then, in the 1930s, the Polish-born American physicist Isidor Isaac Rabi (1898-1988) developed a technique for measuring nuclear magnetic resonance (NMR).
The technique relies on the fact that the nuclei of all atoms are electrically charged. Many nuclei also have spin, which causes them to behave like a magnet. If a nucleus with spin is subjected to the influence of an external magnetic field, it makes a quantum jump to a higher energy level. In order to do so, it must absorb energy in the form of electromagnetic radiation. The energy must be at a specific frequency (called the resonance frequency), which will be dependent on the strength of the magnetic field and the magnetic properties of the particular isotope involved (the term isotope refers to the number of neutrons in the nucleus, which can vary, as opposed to the number of protons, which is fixed for a particular element).
The nucleus falls back to its original energy level by re-emitting the energy it absorbed, again in the form of electromagnetic radiation, and at the same resonance frequency. This electromagnetic radiation, which occurs at microwave frequencies, can be detected, and its frequency measured. Apparatus capable of generating electromagnetic radiation at microwave frequencies became available from the 1930s onwards. A prototype device that used an ammonia maser (an acronym for an acronym for microwave amplification by stimulated emission of radiation) was built in 1949 at the National Bureau of Standards in the US, and although not significantly more accurate than existing quartz clocks, it paved the way for further research.
The breakthrough came in 1955 with the development of an atomic clock based on caesium-133. This clock was built at the National Physical Laboratory in the UK by the English physicist Louis Essen (1908-1997) in collaboration with the US Naval Observatory and with the help of fellow physicist Jack Parry. The frequency of the electromagnetic radiation emitted by caesium-133 was measured in relation to Ephemeris Time (see above), which defined the second as a fraction of a solar year (the Earth's orbital period around the Sun). Within five years the National Standards Bureau in the US had completed its own atomic clocks based on caesium.

NBS-1 - the first caesium atomic clock built by the US National Bureau of Standards
The kind of atomic clock currently used to maintain national frequency standards is called a caesium fountain clock. At the time of writing, two of these clocks serve as the primary time standard for the United States - NIST-F1, which has been operational since 1999, and NIST-F2, which was brought online in 2014. Although the accuracy of NIST-F2 is still being evaluated, if it lives up to expectations, it will not gain or lose more than a second in over three hundred million years!
The caesium fountain clock gets its name from the fact that it throws a cluster of caesium atoms (consisting of about ten million atoms!) upwards inside a vacuum chamber, and then allows them to fall. The movement of the caesium atoms inside the chamber thus somewhat resembles the movement of water in a fountain. But why exactly is this happening? We'll try to explain the principles without going into too much detail.
Caesium is a chemical element (an alkali metal, to be precise). It has a relatively low melting point (28° C), and is one of only five elemental metals that are liquid at, or close to, room temperature. It is thus relatively easy to introduce caesium atoms into the vacuum chamber in a gaseous state, forming a kind of cloud. Once the caesium atoms are in the vacuum chamber an array of six lasers, mounted at right-angles to one another as shown below, push the atoms together to form a ball (this is known as an optical trap). In the process, they slow down the movement of the atoms, causing their temperature to drop to almost absolute zero - a process known as laser cooling.

Caesium atoms in the vacuum chamber are cooled and pushed together into a cloud by lasers
(Image: www.nist.gov)
The two vertical lasers are then employed to push the ball of caesium atoms upwards through the vacuum chamber for a distance of about one metre as shown in diagram (a) below. On their way up, the atoms pass through a microwave cavity (or radio frequency cavity) which is flooded with microwaves generated by a microwave oscillator. The microwaves bounce around inside the cavity, interacting with the caesium atoms as they pass through the chamber. All of the lasers are then turned off, and the atoms fall back down through the vacuum chamber under the influence of gravity, passing once more through the microwave cavity as shown in diagram (b). The interaction of the microwaves with the atoms may or may not cause the energy state of the atoms to change, depending on the frequency of the microwaves.

Caesium atoms move up and down the vacuum chamber, passing through the microwave cavity
(Image: www.nist.gov)
Once the caesium atoms return to their starting point, another laser is fired at them. As a result, any atoms whose state has been altered by their encounter with the microwave radiation will emit light particles called photons. The resulting fluorescence (light emitted by a substance being stimulated by electromagnetic radiation) can then be measured by a detector. The entire process thus far described takes approximately one second.

A laser directed at the caesium atoms may cause them to emit light that can be detected
(Image: www.nist.gov)
The important thing to realise here is that, the closer the frequency of the microwaves is to the resonance frequency of the caesium atoms, the greater the number of caesium atoms that will achieve a higher energy level. Any atoms with an increased energy level will emit photons when a laser is directed at them, and the total number of atoms emitting photons will determine the amount of fluorescence detected. The process is repeated many times while the frequency of the microwaves generated by the microwave oscillator is adjusted up or down in order to establish the frequency that produces the most fluorescence. This frequency will be the resonance frequency of the caesium atom (the frequency used to define the SI second).
The accuracy of an atomic clock depends in part on the temperature of the atoms used. The atoms should be in their lowest energy state at the start of the process, which is only achieved when the atoms are at a temperature of just above absolute zero. The more slowly the atoms move, the colder they will be, since the temperature of a particle is directly related to its kinetic energy. And, while it might sound odd to think of a laser beam cooling something down (we usually associate lasers with heat), you have to bear in mind that a laser beam is a stream of photons (light particles), and photons have momentum.
An atom in the path of a laser beam will absorb and then re-emit photons. If the photon and the atom are travelling in opposite directions, the absorption of a photon will reduce the momentum of the atom by the same amount as the momentum lost by the photon. The atom will re-emit the photon (thus gaining some momentum), but in a random direction. If all of the photons were to strike the atom head on, the overall effect would be to slow the atom down considerably. There is however a problem, because an atom travelling directly away from a photon when absorption takes place can actually increase its momentum in that direction. Since the movement of the atoms in a vacuum tube will be somewhat unpredictable, this could be a problem.
Fortunately, there is a solution. This involves setting the frequency of the laser to a level slightly below the frequency at which photons will most readily be absorbed by the atom (called the resonance absorption frequency). Thanks to the Doppler shift effect, photons approaching the atom head on will appear (from the atom's perspective) to be at or close to the resonance absorption frequency, and are thus readily absorbed. Photons approaching the atom from the opposite direction will appear to have a much lower frequency, and consequently are not so readily absorbed.
When a caesium fountain atomic clock is first turned on, there will be a short delay while the microwave oscillator stabilises itself using a feedback signal from the photon detector, but once the microwave oscillator has been tuned to the correct frequency (i.e. the resonance frequency of caesium-133), digital counters can be used to produce an accurate clock signal. This time signal is then broadcast to the world by a time signal radio transmitter.
Caesium is not the only element that can be used in an atomic clock. Commercial atomic clocks based on hydrogen are available at a cost of about three hundred thousand dollars, for example (for the sake of comparison, the cost of NIST-F1 is estimated to be around one million dollars, according to some sources). These devices are relatively complex to build and do not have the same degree of precision as caesium clocks due to the fact that they operate at a much lower frequency, but they provide a very stable output, and have a comparatively low power consumption (about 100W as opposed to somewhere around 500 W for NIST-F1).
Atomic clocks based on rubidium (another alkali metal) are not as accurate as caesium clocks, but they have the advantage of being cheap, compact, and power efficient. They are eminently suitable for portable applications, and prices start at under a thousand US dollars. Rubidium clocks are often used to provide secondary frequency standards (a secondary frequency standard is a frequency standard that does not have inherent accuracy, and must be calibrated against a primary frequency standard). Typical applications of rubidium clocks include controlling the frequency of television and radio broadcasting stations and mobile telephone network base stations.
In August 2004, NIST unveiled the world's smallest atomic clock, the core of which (sometimes referred to as the "physics package") was described as being the size of a grain of rice, with a power consumption of around 75 mW. The clock uses caesium vapour confined within a sealed cell, which is probed using a tiny infrared laser. Although less accurate than a caesium fountain clock, the new "chip-scale" clock was claimed to be a thousand-fold improvement on quartz oscillators of comparable size, gaining or losing less than a second in three hundred years. It was envisaged that the device could be used in countless portable applications, including battery-powered handheld devices.
In potential applications, a chip-scale atomic clock would probably be coupled to an external quartz oscillator, with the whole package occupying about one cubic centimetre. The physics package could eventually be mass-produced, using the same kind of manufacturing techniques used for other microelectronic systems. This would reduce costs considerably, and make it relatively easy to integrate a chip-scale atomic clock into an existing electronic product. We could, for example, see chip-scale atomic clocks replacing the quartz crystal oscillators currently used in computers. The first commercially available Chip Scale Atomic Clock (CSAC), introduced in 2011, was the Quantum SA.45s Chip Scale Atomic Clock from Symmetricom Inc (now part of Microsemi Corporation), priced at around fifteen hundred US dollars.

The Symmetricom Quantum SA.45s Chip Scale Atomic Clock
