Bits, Bauds and Bandwidth
Overview
The study of telecommunications encompasses a vast range of technologies and concepts. As you might expect, therefore, it also comes with a huge amount of technical jargon, the meaning of which can often vary depending on context. This is particularly true when it comes to the question that is often uppermost in the mind of many end users, which is: "How fast is my data connection?"
The connection in question could be a workplace network connection, a home Internet connection, or the connection between a smartphone and the mobile network. End users don't tend to think that much about the limitations imposed by hardware or data networks as long as they can access the data they want, when they want it, without encountering any problems.
From the point of view of the organisations and individuals responsible for designing and building telecommunications networks, manufacturing network and end-user equipment, administering enterprise network systems, or delivering content, it is of critical importance to understand both the capabilities of, and the limitations imposed by, the available technologies.
Ultimately, we need to ask ourselves two questions: how much data do we need to move from A to B in a given time frame, and how do we achieve the necessary capacity - preferably with some contingency built in - to allow us do so. In order to determine what capacity we need in order to satisfy our requirements, we need to know the volume of the data traffic we will be dealing with. We also need to know what our options are in terms of carrying that traffic.
We can't always say with any certainty how much data will need to be carried over a particular channel at any given time, because this can vary seasonally, monthly, weekly, daily, or even from one minute to the next, depending on how many users are using that channel, and what kind of data is being sent and received. Often, it's a case of making an informed guess based on projected use cases, including estimates of average throughput and worst-case scenarios.
When it comes to equipment or overall channel capacity, there is a great deal more certainty. We can consult technical manuals for network and end-user equipment to establish its data-handling capabilities, and we can similarly consult manufacturer specifications, data sheets or service provider specifications in order to determine the data-carrying capacity of different types of network cable or Internet connection. In order to interpret the information provided, however, we need to have a good grasp of the terminology used to describe those features.
The binary digit
Today, virtually all data communications, and an increasing proportion of radio and television broadcasts, are transmitted digitally. The digital data may be transmitted using a stream-oriented protocol which sends data as a continuous flow of bytes (e.g. Internet streaming media, or digital radio and television broadcasts), or using a message-oriented protocol that sends the data in discrete chunks (e.g. packets, datagrams or frames). All of the data sent, however, consists of a sequence of binary digits - more often referred to as bits.
The bit is the elemental building block of the digital data world. A single bit can represent one of two binary values - zero or one. On its own, a bit can't convey very much information, but several bits grouped together can represent numbers, alphanumeric values, punctuation characters, control characters, and other symbols. If we string enough bits together, we can represent any kind of information, including text, graphics, complex data, photographic images, audio files, and video. The only real limitation is the speed with which we can move all these bits from one place to another.
The monochrome digital image below uses a single bit to represent each pixel. The image is still recognisable as a cat, despite the fact that each pixel can only be either black or white. The overall dimensions of the image are 540 × 400 pixels, giving a nominal file size of 216,000 bits or 27,000 bytes. The image has been saved using the .gif file format, which uses run-length compression to reduce file size. In this case, the file size has been reduced to 6,960 bytes.

A digital image of a cat with a colour depth of 1 bit per pixel
The speed at which data can be carried on a transmission medium will of course depend upon the properties of the transmission medium and the manner in which the signal is encoded - topics we will be looking at in some detail elsewhere. For now, we'll examine what the numbers quoted by service providers and equipment manufacturers actually mean. At the time of writing, for example, British Telecom are offering a range of "Superfast" and "Ultrafast" fibre broadband packages with quoted average download speeds of between 36 Mb and 300 Mb.
Use of the word "average" implies that customers can expect the speed to vary, which is inevitable given the fact that the actual speed at any given time will depend on demand, with the speed of an individual connection being significantly lower at peak times. For non-fibre services, it will also depend on the area in which the customer is located, the type of cabling serving that area, and how far the customer's home or business is from a telephone exchange.
Having established that, however, what does a figure like "300 Mb" actually mean? We said earlier that a sequence of bits can carry more complex information than a single bit on its own. The smallest coherent unit of data is the binary octet - a grouping of eight bits, usually referred to as a byte. Historically, the number of bits in a byte has varied from one hardware implementation to another, but the de facto standard today defines the byte as a grouping of eight bits. When we use the term "byte" in these pages, we are referring to the eight-bit version.
The number of abbreviations used to label digital units can be bewildering. And, just to complicate matters, the terms those abbreviations stand for can mean slightly different things in different contexts. For example, in computer science, byte multiples are usually defined in terms of binary powers. Take the term "kilobyte", for example. In the field of computer science, the kilobyte (together with other units used to describe digital memory capacity) is expressed as a power of two. The kilobyte is thus defined as 210 or 1,024 bytes. The use of the kilo prefix is thus slightly misleading, since the International System of Units (SI) defines the prefix kilo as denoting a multiple of one thousand (1,000 or 103).
Towards the end of the 1990s, the International Electrotechnical Commission (IEC) made recommendations for a set of binary prefixes specifically for powers of 1,024. The terms kibibyte (KiB), mebibyte (MiB) and gibibyte (GiB) were introduced in order to denote 1,024 (210), 1,048,576 (220), and 1,073,741,824 (230) bytes respectively. The SI prefixes kilo, mega and giga were henceforth to be used for only to represent one thousand (103), one million (106), and one billion (109) bytes respectively.
Unless otherwise stated in these pages, the prefixes used should be interpreted according to their SI definition. For example, the term "kilobyte" should be taken to mean one thousand bytes, and not one thousand and twenty-four bytes. The following table lists the units commonly used for describing data transmission rates:
| Unit | Abbr. | No. of bytes | No. of bits |
|---|---|---|---|
| Bit | - | - | 1 |
| Byte | - | 1 | 8 |
| Kilobit | Kb | - | 103 |
| Kilobyte | KB | 103 | 8 × 103 |
| Megabit | Mb | - | 106 |
| Megabyte | MB | 106 | 8 × 106 |
| Gigabit | Gb | - | 109 |
| Gigabyte | GB | 109 | 8 × 109 |
| Terabit | Tb | - | 1012 |
| Terabyte | TB | 1012 | 8 × 1012 |
Let's return to the question of what the term "300 Mb" actually means. Using the table above, we can see that the abbreviation "Mb" - with a lower case "b" as opposed to an upper case "B" - represents megabits, and not megabytes. We therefore have a speed of 300 megabits, or 300 million bits, per second. To get the number of bytes this represents, we need to divide that number by eight (because there are eight bits in a byte). So the average download speed of BT's fastest broadband offering currently is 37.5 million bytes (or 37.5 megabytes) per second.
This kind of download rate is quite impressive, especially for those of us who remember the days when a standard home Internet connection invariably involved a 56k modem, and download times were sometimes measured in days, but it needs to be seen in context. The demand for online content has exploded in the last few years, and a single HD movie can take up anything from 3 to 4.5 gigabytes. Twenty years ago, the average PC didn't even have a hard drive that big!
Bit rate vs. baud rate
People sometimes confuse the term bit rate (or data rate, or data signalling rate) with baud rate (or symbol rate or signalling rate). All of these terms can actually refer to the same values, depending on the properties of the transmission line and the type of transmitter being used, but more often than not they refer to different numbers.
Note also that the terms signalling rate and data signalling rate should probably be avoided when talking about transmission speeds, since they are easily confused with one another and often misunderstood. We prefer the term baud rate (or symbol rate) over signalling rate, and bit rate rather than data rate or data signalling rate. The baud is named after the French telegraph engineer Jean-Maurice-Émile Baudot (1845- 1903), who invented the Baudot telegraph code.
Before we proceed, let's look at some definitions:
- Baud rate (or symbol rate) - the number of symbols transmitted per second.
- Symbol - a distinct and detectable state of the transmission medium such as a voltage level or waveform that persists for a fixed period of time.
- Bit rate - the total number of bits transmitted per second.
- Gross bit rate - also called the digital signalling rate, this is the total number of bits transmitted per second including overhead.
- Net bit rate - the total number of bits transmitted per second excluding overhead.
Note that the term bit rate, when used on its own, usually means the same thing as gross bit rate, i.e. the total number of bits transmitted over the transmission medium per second, regardless of how many of those bits represent actual data, and how many are used to carry control information (usually referred to as overhead).
A symbol is a signalling element that can be detected by a receiver. The data being transmitted may be represented by the symbol itself or, as is sometimes the case, by the transition between two signalling elements. In most cases, the symbol itself is used to represent one or more bits. The number of bits that can be represented by a symbol depends on how many different symbols can be represented by the data encoding scheme used.
Symbols are typically represented either by a change in voltage on a transmission line (baseband signalling) or by changes in the phase, frequency or amplitude of an analogue carrier signal (passband signalling, also known as carrier-modulated signalling). If two signalling levels are used, each element will represent either a one or a zero; only one bit of information is encoded in each symbol, and the baud rate and the bit-rate are the same. If more than two signalling levels are used, however, it becomes possible to encode more than one bit per signal element.
Let's suppose that, instead of representing one bit per symbol, we want to represent two bits per symbol. How many different symbol do we need? We need to consider how many different possible permutations there are for a two-bit number:
00
01
10
11
There are four possible permutations, so we would need to be able to represent four different symbols, one to represent each possible combination of two bits. Let's continue the process by looking at how we would represent three bits per symbol. Here are the possible permutations:
000
001
010
011
100
101
110
111
There are now eight possible permutations, so we would need eight different symbols to represent any combination of three bits using a single symbol. There is already a pattern emerging here, which is that for each additional bit per symbol we add, we need to double the number of symbols. That sounds easy enough, but there are some practical implications to consider.
In order to send the required number of bits per symbol, we need a transmitter capable of generating the necessary number of different symbols (as different voltage levels or waveforms, or whatever). We also need a receiver sensitive enough to differentiate between those symbols. Furthermore, we will require a transmission medium that is capable of carrying the resulting signal from source to destination whilst maintaining sufficient signal integrity for it to be correctly interpreted by the receiver.
Digital bandwidth
Unlike the bandwidth of an analogue transmission channel, which is usually defined as the difference between the highest and lowest frequencies that the channel can support measured in hertz, the digital bandwidth of a channel, sometimes called the bit rate, is expressed in bits per second, or some multiple thereof. Most data channels today support bitrates in the tens, hundreds, and even thousands of megabits per second.
Current research is progressing at such a pace that we hesitate to quote figures for the highest per-channel bitrate currently possible, because whatever figure we give will probably be out of date before we publish this article. Suffice to say that in 2018, Japan's National Institute of Information and Communications Technology (NICT) and the Tokyo-based electronics company Fujikura Ltd. demonstrated an optical fibre capable of transmitting data at a bit rate of 159 Terabits per second (that's 159 trillion bits per second) over a distance of more than one thousand kilometres!
The data rates most of us get on our local area network, Internet, or mobile network connections are somewhat more pedestrian, but still pretty fast in most cases. The following table lists some of the most widely used network and internet connection types, together with the theoretical maximum bitrates they support.
| Connection Type | Standard | Bitrate | Description |
|---|---|---|---|
| Standard Ethernet | IEEE 802.3i (10BASE-T) |
10 Mbps | Standard Ethernet over twisted pair cable. Still used in some local area networks and home networks, although it has generally been replaced by Fast Ethernet and Gigabit Ethernet. |
| Fast Ethernet | IEEE 802.3u (100BASE-TX) |
100 Mbps | Fast Ethernet over twisted pair cable. Commonly found in local area networks and home networks using Category 5 (Cat-5) copper twisted-pair cable. |
| Gigabit Ethernet | IEEE 802.3ab (1000BASE-T) |
1 Gbps | Gigabit Ethernet over twisted pair cable. Originally developed for use in large computer networks to connect servers, routers and switches. Gradually replacing Fast Ethernet as the most widely used connection type in local area networks. Uses Category 5e (Cat-5e) copper twisted-pair cable. |
| WiFi | IEEE 802.11n | 600 Mbps | Wireless network connections are frequently used in home networks. They are also used to provide wireless network connectivity in offices and on public transport, as well as in public spaces such as hospitals, schools, universities, airports and restaurants. Most of the IEEE 802.11 standards work over distances of up to 30 metres, although data rates tend to fall off with distance. The IEEE 802.11n standard (sometimes called WiFi 4) uses frequencies in the 2.4 GHz and 5 GHz ranges. IEEE 802.11n is not the fastest WiFi connection currently available, but it is (at the time of writing) the most widely deployed. It is also (optionally) backwards compatible with earlier implementations. |
| Dial-up | ITU-T V90/V92 |
56 kbps | Dial-up Internet connection over analogue telephone lines using a 56k modem. Still used in some rural areas where broadband is not available. |
| ISDN | ISDN BRI | 128 kbps | Integrated Services Digital Networks Basic Rate Interface. Provides a 64-bit digital voice channel and a 64-bit Internet connection. Once widely deployed in Germany, France and to a lesser extent in the United Kingdom to provide digital telephony, fax services, and Internet access over analogue telephone lines. ISDN has mostly been replaced in these areas by Digital Subscriber Line (DSL) technology. |
| Mobile Internet | 4g | 300 Mbps | Fourth generation mobile Internet technology. A 4g mobile connection is currently the fastest mobile Internet connection available to most users, although implementation of 5g mobile networks is under way. |
| ADSL2/2+ | ITU G.992.3/ G.992.5 |
12 Mbps/ 24 Mbps |
Asymmetric Digital Subscriber Line. A digital subscriber line (DSL) technology that provides broadband Internet access over an analogue telephone line using a range of frequencies above those used for standard telephony. Bitrates are asymmetric (download data rates are much higher than upload data rates). A DSL filter (or splitter) is used at the consumer's premises to separate digital data and standard voice signals. An ADSL modem/router provides the interface between the DSL filter and end user devices. Installations are limited to premises in relatively close proximity to a telephone exchange (typically 4 kilometres or less). |
| Cable broadband | DOCSIS (Data Over Cable Service Interface Specification) |
20-100 Mbps | Cable Internet access. Uses cable television infrastructure to provide Internet access to consumers. A cable modem at the customer's premises provides the interface between the incoming connection and end user devices. A coaxial cable connects the customer premises to the service provider's cable modem termination system (CMTS) over distances of up to 160 kilometres. Most cable modems restrict upload and download rates to limits set by the cable provider and stored in configuration files that are downloaded to the modem when it connects to the cable provider's equipment for the first time. Usually, a number of users in the same residential area will share the available bandwidth for that area. Cable operators must monitor usage patterns and if necessary adjust the level of bandwidth available to ensure that customers receive adequate service at peak usage times. |
| Fibre to the cabinet | FTTC/VDSL | 40-80 Mbps | A Digital Subscriber Line Access Multiplexer (DSLAM) is housed in a street cabinet in the proximity of end user premises, and is connected to a telephone exchange via a high-speed fibre-optic cable, effectively moving the exchange equipment much closer to the user. The link between the cabinet and the subscriber's home or premises utilises Very High Speed Digital Subscriber Line (VDSL) technology over the existing twisted pair copper wires. Although much faster than ADSL connections, access speeds are still dependent on the distance between the cabinet and the subscriber's home or premises. |
| Fibre to the premises | FTTP | 100-1000 Mbps | A high-speed optical fibre connects the subscriber's home or premises to the telephone exchange, eliminating the copper cable traditionally used in the subscriber loop (or "last mile"). Connection speeds are not affected by the distance between the subscriber's home or premises and the telephone exchange. The fibre-optic cable from the exchange is usually terminated by a fibre modem at the subscriber's premises, which is connected to a broadband router via an Ethernet connection. |
It should be noted that the bitrates given above are the maximum gross bit rates theoretically achievable. Actual gross bitrates can be significantly lower, depending on various factors. This is especially true of Internet connections where bandwidth may be shared among a number of end users (as with cable Internet access), for broadband Internet connections that employ twisted pair copper cables in the subscriber loop, where distance from the exchange (in the case of DSL) or cabinet (in the case of FTTC) will be a factor, and for mobile Internet connections where both distance from an access point and environmental factors will have a significant impact.
Regardless of the type of channel used, average data rates will be significantly lower than average gross bitrates. This is because the transmitted data will include the signalling and control data (known as protocol overhead) necessary to ensure that the data reaches the correct destination, and that the data received is complete and error-free.
Digital bandwidth can be likened to the rate at which water flows through a pipe, where the diameter of the pipe is analogous to the digital bandwidth of a channel. Instead of litres per second, we measure the follow of data in thousands of millions of bits per second. The maximum amount of data that can be transmitted over a network or Internet connection per unit time represents the maximum bandwidth of that connection, in the same way that the maximum amount of water flowing through a pipe represents its maximum flow rate.
The diagram below represents this analogy. The diameter of each "pipe" is proportional to the maximum bitrate achievable on various types of network and Internet connection. Note that all of the bitrates shown are theoretical maximum values. The actual date rates achieved will be significantly lower, especially so in the case of dial-up, ADSL, mobile broadband and WiFi Internet connections where distance, either between subscriber premises and a telephone exchange or between a wireless transmitter and receiver, will be a significant factor in determining the actual data rates achieved.
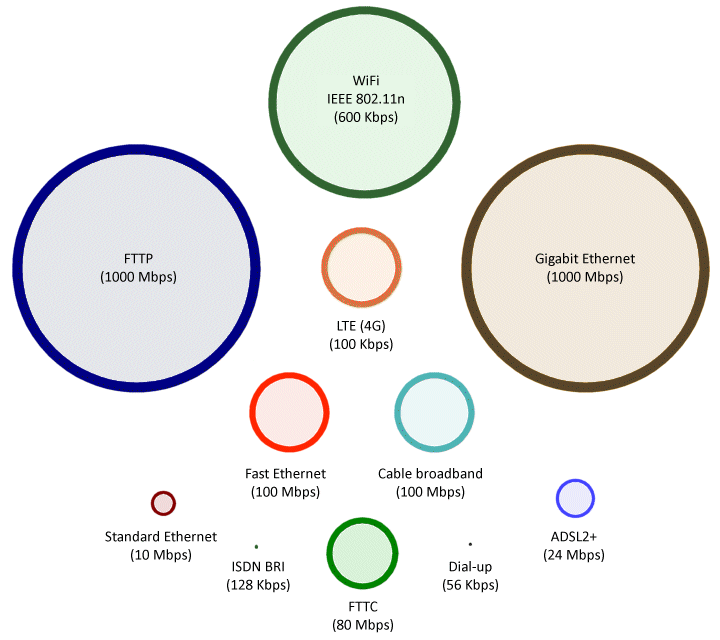
Comparative maximum bitrates of various network and Internet connection types
In July 2004, IEEE Spectrum Magazine published an article that cited a new law relating to digital bandwidth that is believed to have first been proposed by Phil Edholm, who at the time was chief technology officer and vice president of network architecture enterprise for the now defunct Nortel Networks Corporation. Edholm describes three kinds of telecommunication bandwidth - fixed wired bandwidth, nomadic bandwidth (bandwidth used by people moving between wireless access points), and mobile wireless bandwidth.
Edholm's law states that these three types of bandwidth increase at the same exponential rate, approximately in proportion to one another (and also converging, as wireless network technology gradually catches up with wired networks). According to Edholm's law, both the total capacity and the data rate for each type of bandwidth will double every eighteen months. The relevant information on bandwidth and data rates for the last four decades would appear to support this assessment.
Analogue bandwidth
In general terms, analogue bandwidth is the difference between the highest and lowest frequency supported by a transmission medium, the difference between the upper and lower frequency bounds of a communications channel, or the difference between the highest and lowest frequency contained in a transmitted signal, measured in hertz. The term analogue in this context does not imply that the transmitted signals are analogue signals (although they could be). In fact, virtually all transmitted signals, whether analogue or digital, will occupy a band of frequencies with a non-zero width.
An analogue telephone circuit is a good example of a telecommunications channel that has been artificially bandwidth-limited. Most subscriber loops in the public switched telephone network still consist of copper twisted pair links, over which analogue voice signals are transmitted in the form of a constantly varying voltage.
The frequencies found in the human voice range from around 100 Hz at the lower end to 20 kHz at the upper end, although various tests have shown that the human ear cannot detect frequencies greater than about 12 kHz. Indeed, the frequencies to which the human ear is most sensitive are concentrated in the frequency range 300 Hz to 3 kHz. Consequently, the range of frequencies used for analogue voice telephony has its lower bound at 300 Hz and its upper bound at 3.4 kHz - a total bandwidth of 3.1 kHz.
The twisted pair copper wire cables used for telephony will actually support much higher frequencies, which is why they can be used to carry ADSL signals. Standard ADSL and ADSL2, for example, use the frequency range 25.875 kHz to 138 kHz for upstream traffic, and the range 138 kHz to 1.104MHz for downstream traffic. Frequency division multiplexing is used to split the bandwidth into individual channels, each of which has a bandwidth of 4.3125 kHz, giving 26 upstream channels and 224 downstream channels.

ADSL and ADSL2 bandwidth allocation
For ADSL2+, the overall bandwidth allocation is doubled to 2.208 MHz. There are 32 additional upstream channels, occupying the frequency range 138 kHz to 276 kHz, and 448 downstream channels that take up the rest of the bandwidth allocation (276 kHz to 2.208 MHz). Each channel in the ADSL frequency band is used in a similar fashion to the way in which the (circa) 4 kHz frequency band normally reserved for voice telephony is used for dial-up connections.
Each ADSL channel can theoretically carry up to 56 kbps per second, which would give a potential maximum downstream bit rate of just over 25 Mbps. This is rarely if ever achieved in practice, because the signals attenuate (weaken) as the distance between the subscriber and the local exchange increases, which means they become more susceptible to noise. In addition, some frequencies are more susceptible to noise than others, particularly at the higher end of the frequency range, so some channels will be used at a lower bitrate than others (or may not be used at all).
Channel capacity
We saw above that, for ADSL, each individual channel has the same analogue bandwidth, and the same amount of data can (potentially) be transmitted over each channel. This highlights an underlying principle of telecommunications, which is that the amount of information that can be transmitted over a given channel is proportional to the analogue bandwidth of that channel, regardless of the actual frequencies involved.
This principle is embodied in Hartley's law, named after the American information theorist Ralph V. R. Hartley (1888-1970) who first proposed it while working at Bell Laboratories. In his 1928 paper "Transmission of Information", Hartley stated that "the total amount of information that can be transmitted is proportional to frequency range transmitted and the time of the transmission."
Hartley's law does not fully describe the behaviour of a fixed-bandwidth channel because it does not take into account factors such as noise but it, together with the work of Nyquist (see below), formed the basis for a more complete theory of information and transmission formulated by the American mathematician and electrical engineer Claud Shannon (1916-2001), whose landmark paper on the subject, "A Mathematical Theory of Communication", was published in 1948 (we will be looking at Shannon's work in the field of telecommunications elsewhere in this section).
In 1927, the Swedish-American electronic engineer Harry Nyquist (1889-1976) had determined that the maximum number of independent pulses that could be sent over a telegraph channel per unit time is equal to twice the analogue bandwidth of the channel. This idea can be expressed mathematically as:
f p ≤ 2B
where f p is the maximum number of pulses per second and B is the bandwidth in hertz. The quantity 2B would later become known as the Nyquist rate. Nyquist published his findings in his 1928 paper "Certain topics in Telegraph Transmission Theory".
Hartley's work was focused on quantifying the number of distinct voltage levels at which pulses could be transmitted over a given channel. He reasoned that this must depend at least in part on the ability of the receiver to distinguish between different voltage levels (i.e. the sensitivity of the receiver) and the dynamic range of the received signal (in this context, the range of voltages that the receiver can actually detect).
Hartley asserts that each distinct voltage level can carry a different message. If the dynamic range of the transmitted signal is restricted to ±A volts, and the sensitivity of the receiver is ±V volts, then the maximum number of unique messages M is given by:
| M = 1 + | A |
| ∆V |
As you probably realise, Hartley's "messages" equate to signal symbols and, as we saw earlier in this article, the number of bits we can encode per symbol depends on the number of different symbols we can transmit, which in turn depends on the number of different signal levels we can generate. For a one-bit message, we need two signal symbols; for a two-bit message, we need four signal symbols; for three bits we need eight symbols, and so on. Hartley's maximum line rate (or data signalling rate) R can thus be expressed as:
R = f p log 2 (M)
where f p is the Nyquist rate (or pulse rate or symbol rate or baud).
As we saw above, Nyquist had already established that the number of pulses it was possible to transmit on a channel is twice the analogue bandwidth in hertz. Hartley was thus able to combine his formula with that of Nyquist to obtain a new formula, giving the maximum data signalling rate based on channel bandwidth:
R ≤ 2B log 2 (M)
Hartley's formula makes no provision for factors such as noise, but it does correctly indicate that the data signalling rate achievable for a given channel will be proportional to the channel's analogue bandwidth. It also provides the basis for Claude Shannon's later work.
Baseband bandwidth
The bandwidth of a signal generally falls into one of two categories - baseband or passband. In baseband signalling, the frequencies used match those of the information itself. For example, the frequencies used in the local loop of the public switched telephone network for analogue voice signals, (300-3400 hertz), are the actual frequencies produced by the human voice. The bandwidth of a baseband signal is usually considered to be equal to the highest frequency in that signal.
Wired local area networks also use baseband signalling to carry digital information, which is why most Ethernet standards (10BASE-T, 100BASE-TX, 1000BASE-X etc.) include the word BASE. The fundamental frequency of an Ethernet signal matches the symbol rate used to transmit digital information over a single coper wire twisted pair or fibre optic link (we'll expand on the implications of the term fundamental frequency in due course).
The simplest form of baseband digital signalling (sometimes called line coding) uses a unipolar encoding scheme in which a binary one is represented by a positive voltage, and a binary zero is represented by the absence of a voltage. This kind of encoding scheme is analogous to on-off keying - a simple form of amplitude-shift keying (ASK) in which digital data is represented by the presence or absence of a carrier sine wave.
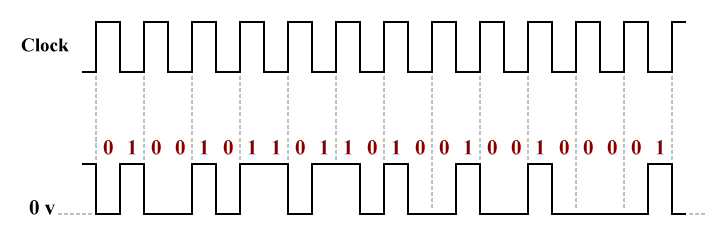
Simple unipolar binary encoding
The diagram above shows a sequence of bits encoded using a non-return-to-zero (NRZ) unipolar encoding scheme, so called because the voltage does not return to zero during the middle of a bit period as in some other encoding schemes. This effectively means that two bits can be transmitted during each clock cycle. A binary one is represented by a square wave pulse, and a binary zero is represented by the absence of such a pulse.
This is a very simple encoding scheme that makes for efficient use of available bandwidth, but it has some major disadvantages. A unipolar signal inevitably results in a significant DC (direct current) component which can lead to signal distortion at the receiver. It can also result in a loss of energy on the transmission line, since the presence of a direct current causes the wires to heat up. Another problem is that there is also no in-built clocking mechanism in the signal, so long sequences of ones or zeros can lead to a loss of synchronisation between the transmitter and the receiver.
The DC component problem can be at least partially solved by using a bi-polar encoding scheme in which (for example) a binary one is represented by a positive voltage, and a binary zero is represented by a negative voltage. There may still be a small DC component if there are more ones than zeroes (or vice versa), but the overall DC component is greatly reduced.
The timing problem can be solved by having the signal return to zero volts after each bit is transmitted. This means that there will be a guaranteed transition, either from a positive voltage to zero or from a negative voltage to zero) after each bit is transmitted. This transition can be detected by the receiver, which uses it as a clock signal. The down side is that only one bit can be transmitted during each clock cycle, so use of the available bandwidth is only half as efficient as for unipolar NRZ encoding.
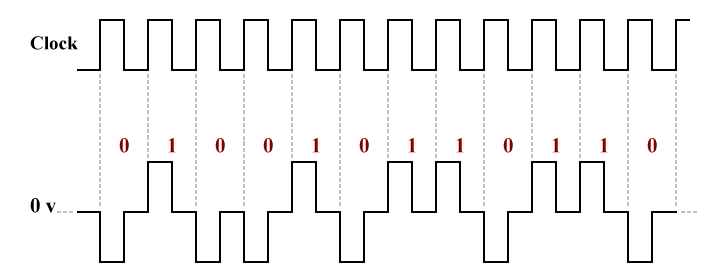
Bipolar return-to-zero (RZ) binary encoding
The other thing to consider here in the context of signal bandwidth is the range of frequencies that must be supported by the channel that must carry the signal. The two line-coding schemes we have seen so far both use square wave pulses to represent binary digits. A square wave pulse is the ideal shape to represent a binary digit because the receiver samples the signal in the middle of each bit time (for NRZ encoding schemes this will be in the middle of each clock cycle, and for RZ encoding schemes it will be in the middle of the first half of each clock cycle).
A square pulse therefore offers the best chance of the receiver being able to distinguish between a binary one and a binary zero, and thus correctly interpret the incoming signal. Unfortunately, generating and transmitting such a pulse turns out to be quite tricky. In fact, it is not physically possible to produce an absolutely square waveform because it would require an infinite range of frequencies to be present in the signal - but we can produce a pulse that is almost square (and hence good enough) using a relatively small number of frequencies.
Square wave pulses do not appear in nature, but the French scientist Jean Baptiste Joseph Fourier (1768 - 1830) was able to demonstrate that, by combining a number of sine waves, each with a different frequency and amplitude, it is possible to create more complex waveforms, one of which is a good approximation of a square wave.
The frequency of the square wave we want to create is said to be the fundamental frequency (we mentioned this term earlier). Fourier showed that by taking a sine wave with the same frequency as the required square wave, and then adding successive odd-numbered harmonics to it, a square wave can be approximated.
A harmonic is a sine wave with a frequency that is an integer multiple of the fundamental frequency. By adding the fundamental, third harmonic, and fifth harmonic together, we can achieve a waveform that is a reasonable approximation of a square wave. Note that the amplitude of each harmonic, as a proportion of the amplitude of the fundamental, is approximately the inverse of its harmonic number. The diagram below shows these three sine waves separately occupying the same time period.
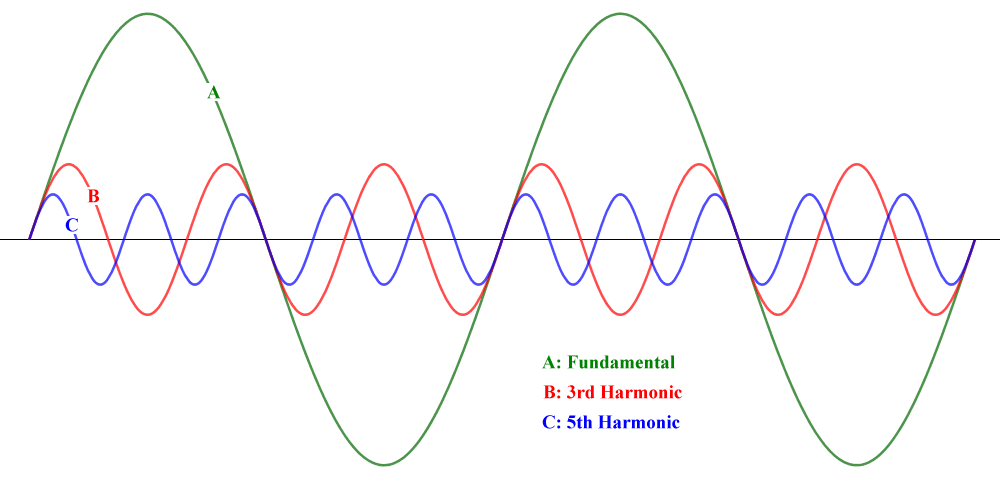
The fundamental, 3rd and 5th harmonics
If we transmit these three sinusoidal waveforms simultaneously on a physical medium, they will add together to produce a new waveform that approximates a square wave, as illustrated by the image below. Since an infinite number of odd harmonics would be required to produce a "perfect" square wave, and since no transmission medium is capable of supporting an infinite range of frequencies, an approximation is the best we can hope to achieve.
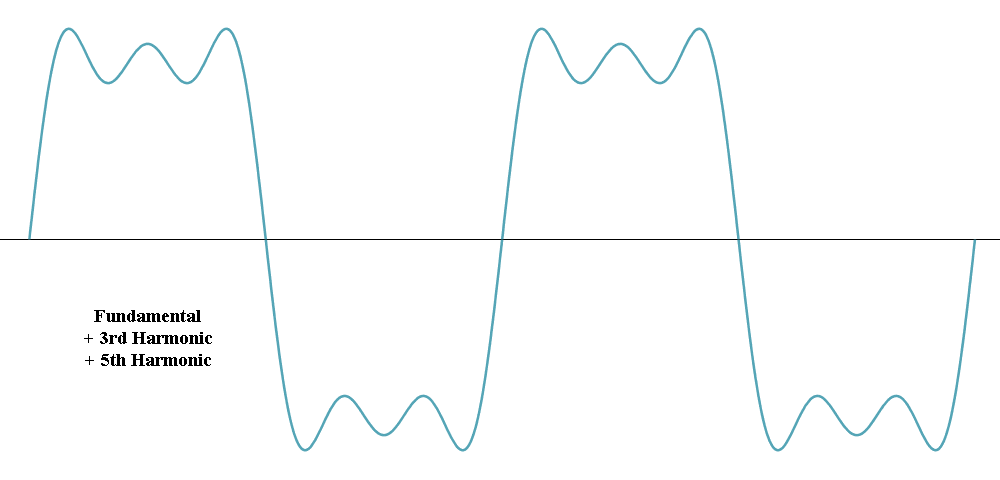
The fundamental and some number of odd harmonics can be used to approximate a square wave
The degree to which we can approximate a square wave on a given channel will largely depend on the power of the transmitted signal and how "noisy" the channel is. Thermal noise (the electronic noise generated by the thermal agitation of electrons) is present in all conducting wires and affects all frequencies. If the power level of the noise at a particular frequency is greater than the transmitted power for that frequency, the receiver will be unable to detect it.
Bear in mind also that electrical signals attenuate (become weaker) as they travel along a wire, whereas the level of thermal noise remains more or less constant throughout the length of the wire. The degree to which a signal is affected by attenuation is related to its frequency; the higher the frequency, the more susceptible it is to the effects of attenuation.
At some point, adding harmonic frequencies to a signal in order to better approximate a square wave becomes unproductive because, by the time the signal reaches the receiver, the signal power for those frequencies will have fallen below the channel's "noise floor". A more detailed discussion of the effects of noise will be undertaken elsewhere. For now, you should simply be aware that real digital signals only vaguely resemble the series of neatly drawn square wave pulses you see in diagrams.
So far, we have looked at the waveform of a complex wave (in this case a square wave) as it might appear on an oscilloscope, which displays the amplitude of a waveform as a function of time. In other words, we have looked at these waveforms in the time domain. We could also look at the waveform using a spectrum analyser, which displays the amplitude and frequency of each sine wave used to generate the complex waveform. Looking at the same square wave illustrated above in the frequency domain (and ignoring noise) we would see something like the image below.
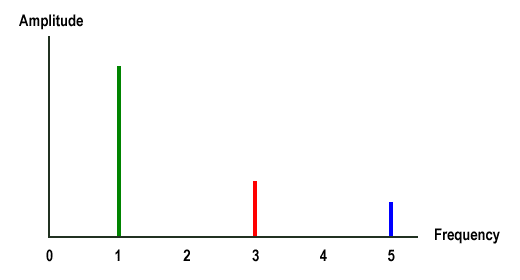
A frequency-domain view of a square wave comprising the fundamental, 3rd and 5th harmonics
More sophisticated signalling schemes use techniques such as pulse amplitude modulation (PAM) to generate square wave pulses at different voltage levels, allowing more than one binary digit to be represented by each pulse and making more efficient use of the available bandwidth (this is the kind of signalling used in 100BASE-TX and 1000BASE-T Ethernet).
Binary digits can also be represented by the transition between two voltage levels. The Ethernet 10BASE-T (10 Mbps) standard uses a form of Manchester encoding in which a binary one is represented by a transition from -1 volt to +1 volt, and a binary zero is represented by the opposite transition, i.e. from +1 volt to -1 volt. The diagram below illustrates the principle:
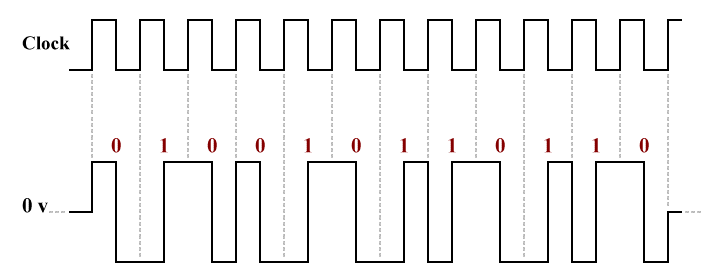
Manchester encoding, as used in 10BASE-T Ethernet (IEEE 802.3i)
Manchester encoding is essentially a bi-polar NRZ encoding scheme that uses a form of modulation called phase shift keying (PSK) that allows the direction of a voltage transition to be reversed as and when required. Because it is guaranteed that there will be a transition in the middle of each clock cycle, the receiver can use the transition to synchronise itself with the transmitter's clock. The signal is thus said to be self-clocking because the clock signal is built in to the line code itself.
As with the line coding schemes we have previously looked at, the waveform produced by Manchester encoding does not resemble its idealised diagrammatic representation particularly closely. In fact, since the binary digits are represented by a voltage transition rather than a specific voltage level, the underlying waveform is essentially a sine wave. If we were to look at how the voltage of an Ethernet 10BASE-T signal varies over time using an oscilloscope, we would probably see something like the following:
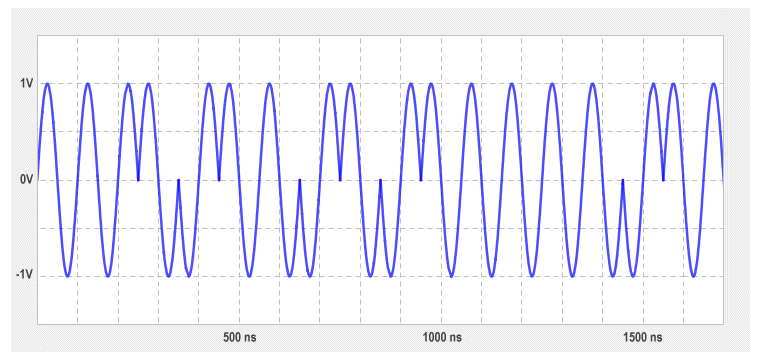
A Manchester encoded digital signal, as seen on an oscilloscope
The signal you would see on an oscilloscope might not be quite so "clean" as the signal we have drawn here, but the illustration still gives you a fairly good idea of what it would look like. Each horizontal division on our oscilloscope screen represents 500 millivolts, so the signal has a positive peak at plus one volt, and a negative peak at minus one volt. The vertical divisions each represent a time interval of 100 nanoseconds. Since a nanosecond is one thousand millionth of a second, each division represents one ten-millionth of a second. This is as it should be, since the 10BASE-T Ethernet standard has a gross bitrate of 10 Mbps.
Let's assume that the signal is sampled every 100 nanoseconds. We can read off the binary digits according to the direction (i.e. up or down) in which the voltage transition is going at the end of each 100 ns interval, starting at the 100 nanosecond marker and ending with the 1600 nanosecond marker. The first two transitions go from low to high, so we start with two binary ones. The next transition is from high to low - a binary zero. Here is the complete sequence:
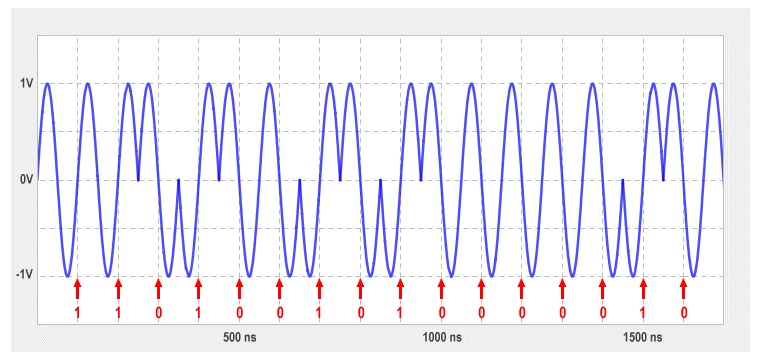
Voltage transitions at 100 ns intervals represent binary digits
In order to change the signalling symbol (i.e. to make the change from a binary one to a binary zero or vice versa), the transition at the end of a 100 nanosecond interval must change direction from low-to-high (or high-to-low) to high-to-low (or low-to-high). This means that the signal must be phase-shifted through π radians (180 degrees).
From a bandwidth point of view, the baseband bandwidth of the signal is 10 MHz because we are effectively modulating a sine wave carrier to generate the line code. No higher frequency signals are needed, because when the receiver samples the signal, it only has to determine whether or not a transition is occurring, and if so, in which direction.
Manchester encoding was not used for 100BASE-TX, mainly for historical reasons. Simply put, the widely deployed Category 5 unshielded twisted pair (CAT 5 UTP) cable installed in the majority of networks when this technology were being developed was not rated for the higher frequencies that would have been used. On the other hand, the relatively low passband bandwidth requirement of 10BASE-T means that it can also be used over category 4 cables (which are rated up to 20 MHz) and even category 3 cables (rated up to 16 MHz).
Passband bandwidth
Almost all sources of information generate baseband signals, and almost all wired local area networks use baseband signalling because the relatively low frequencies involved are less susceptible to attenuation. In most cases, there is no need to apply a bandwidth filter because the entire bandwidth of a channel is dedicated to a single signal. A baseband signal can contain any frequency up to and including the maximum frequency supported by the channel because, unlike various forms of wireless transmission, no antennae are required to transmit and receive signals.
Frequency is a significant factor in wireless communication because the size of the antenna required to transmit a signal increases with wavelength, which is inversely proportional to the frequency of the signal. For example, an antenna capable of transmitting a 10 MHz radio signal would be at least 7.5 metres in length! Relatively low-frequency signals carrying information such as audio and video, and even network data, are thus unsuitable for wireless transmission. In order to transmit this information wirelessly, it must be modulated onto a high frequency carrier wave - which is where passband signalling comes in.
Passband signalling essentially involves taking a baseband signal of some kind and using that signal to modulate a high-frequency carrier wave by varying its amplitude, frequency or phase. AM and FM radio, for example, use amplitude modulation and frequency modulation respectively to superimpose baseband audio signals onto a radio frequency carrier wave.
Although the carrier wave itself is generated at a constant frequency, modulating the carrier wave (and this is true regardless of the type of modulation used) will generate signal frequencies above and below that of the carrier wave frequency, or centre frequency (f centre ). These two sets of frequencies are usually referred to as sidebands, because they extend to either side of the centre frequency. However, not all of these frequencies are useful, or indeed desirable.
It is only necessary to transmit those frequencies that actually play some part in conveying the information contained within the baseband signal used to modulate the carrier. To this end, a filter (usually called a bandpass filter) is used to remove the unwanted frequencies from the modulated signal before it is transmitted.
The highest and lowest frequencies (f H and f L ) allowed to pass through the bandpass filter on either side of the centre frequency are known as the upper and lower cut-off frequencies. The bandwidth of the resulting signal is the difference between the upper and lower cut-off frequencies. In some texts, the signal that enters the bandpass filter is called a passband signal, whereas the signal that emerges from the filter is called a bandpass signal, or sometimes simply bandwidth-limited signal.
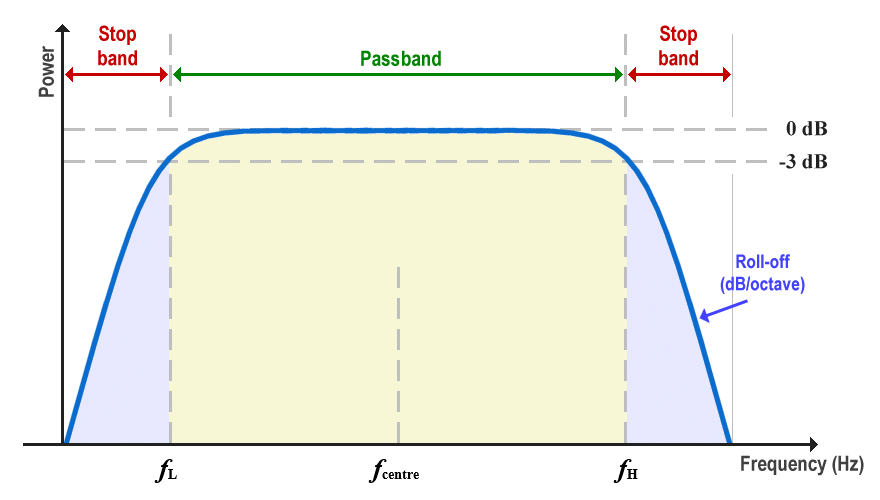
A bandpass filter limits the range of frequencies transmitted
The above diagram shows the effect of a typical bandpass filter on a passband signal. The basic function of a bandpass filter is to allow the passage of all frequencies within a certain range (the passband) and reject (attenuate) any frequencies outside that range. An ideal bandpass filter would allow all signal frequencies between the upper and lower cut-off frequencies to pass through it at some maximum power level, and completely attenuate all frequencies to either side of the passband. In practice, this is not possible.
The cut-off frequencies themselves are usually (though not always) chosen to be the upper and lower frequencies at which the signal power falls below fifty percent of the power at the centre frequency. This figure, although somewhat arbitrarily chosen, is considered to be the point at which the signal ceases to have sufficient power to be useful. As you can see from the diagram, the filter's upper and lower cut off frequencies occur at the points on either side of the centre frequency where the signal has a gain of -3dB, which equates to a fifty percent drop in power.
The filter does not attenuate the frequencies to either side of the cut-off points completely, but there is a fairly sharp "roll-off" in terms of signal power that is usually expressed in dB per octave (an octave is a twofold increase in frequency). The slope of the roll-off depends on the type of bandpass filter used, but the general aim is to make the roll-off as steep as possible without compromising the quality of the bandpass signal itself. The range of frequencies over which roll-off occurs on either side of the passband is called a stop band.
Bandpass filters are used in both transmitters and receivers. The bandpass filter in a transmitter is there to ensure that the transmitted signal does not interfere with signals transmitted by other stations on adjacent channels. The bandpass filter in a receiver accepts signals that contain the specified range of frequencies and filters out unwanted signals, preventing the receiver from becoming overloaded and improving the signal-to-noise ratio of the signal to be decoded.
Bandwidth allocation
Passband signals invariably share a transmission medium with other passband signals. This is true whether they are transmitted over a guided medium such as a coaxial cable (this is the case, for example with cable TV and cable Internet services, which often share the same cable) or an unguided medium such as a satellite or microwave link. In mobile networks, for example, the available bandwidth must often be shared between hundreds, or even thousands of users in a relatively small area.
When multiple signals are sent over a guided medium such as a coaxial cable or optical fibre, some form of multiplexing is used to ensure that each signal has its own channel. For optical fibre, this takes the form of either time division multiplexing (TDM) or wavelength division multiplexing (WDM). For transmitting multiple signals on a coaxial cable, frequency division multiplexing (FDM) is used, in which the available bandwidth is subdivided into multiple non-overlapping channels, each of which uses a different range of frequencies.
Wireless communication is faced with far greater challenges than communication over guided media because it is far more susceptible to interference and noise. In addition, there is fierce competition for wireless bandwidth. In order to ensure continuity of service, and to reduce the possibility of wireless transmissions interfering with one another, the allocation of wireless bandwidth must be tightly controlled.
Different parts of the electromagnetic spectrum have been set aside for applications such as television and radio broadcasting services, satellite communication, mobile telephony, emergency services, maritime communication, air traffic control, and military use. Special frequency bands have even been set aside for amateur radio enthusiasts and electronics hobbyists!
In Europe, although each country's regulatory body has some input into the process, the overall responsibility for coordinating frequency allocation lies with the Electronic Communications Committee (ECC), which is part of the European Conference of Postal and Telecommunications Administrations (CEPT – from the French version Conférence européenne des administrations des postes et des télécommunications). In the United States, frequency allocation is the responsibility of the National Telecommunications and Information Administration (NTIA) and the Federal Communications Commission (FCC).
The body that regulates frequency allocation in the UK is the Office of Communications (Ofcom). Ofcom is the government-approved regulatory and competition authority for the broadcasting, telecommunications and postal industries of the United Kingdom. According to their website, they
" . . . regulate the TV, radio and video on demand sectors, fixed line telecoms, mobiles . . . plus the airwaves over which wireless devices operate".
Ofcom's online version of the UK Frequency Allocation Table (UKFAT), which provides details of how wireless frequencies are allocated in the United Kingdom, can be found here.
