Quadrature Amplitude Modulation (QAM)

Quadrature amplitude modulation (QAM) is a modulation scheme in which two sinusoidal carriers, one exactly 90 degrees out of phase with respect to the other, are used to transmit data over a given physical channel. One signal is called the "I" signal, and can be represented by a sine wave. The other is called the "Q" signal, and can be represented by a cosine wave. Because the carriers occupy the same frequency band and differ by a 90-degree phase shift, each can be modulated independently, transmitted over the same frequency band, and separated by demodulation at the receiver. For a given bandwidth, QAM enables data transmission at twice the rate of standard pulse amplitude modulation without any degradation in the bit error rate. QAM and its derivatives are used in both mobile radio and satellite communication systems. Each symbol is a specific combination of signal amplitude and phase. By combining the amplitude and phase modulation of a carrier signal, it is possible to increase the number of possible symbols and therefore transmit more bits for each symbol. One way to represent the symbols is to use a constellation pattern diagram such as the one shown below. The pattern shown represents the different amplitudes and phases. Dots at 0, 90, 180, and 270 degrees all have two possible amplitudes resulting in eight different symbols. With eight symbols, it is possible to transmit 3 bits for each symbol. For example, if the modulated signal is of amplitude 1 at 0 degrees, three zeros (000) are transmitted.

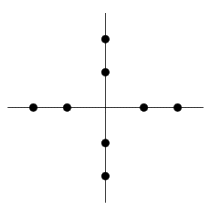
A 3-bit QAM constellation

Modern communication equipment requires modulation that uses dense constellation patterns. The diagram below depicts a 16-state constellation pattern, allowing the transmission of four bits for every baud. The number of states grows exponentially to the number of bits transmitted per baud. Transmitting eight bits per baud would require 256 possible states, resulting in a very dense constellation pattern.

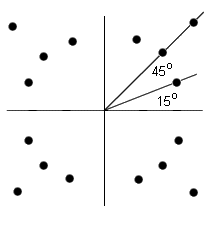
A 4-bit QAM constellation