| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
The extreme value theorem is essentially an extension of the boundedness theorem, which states that a continuous function defined on a closed interval is bounded on that interval. The theorem was first proven during the 1830s by the Bohemian mathematician Bernard Bolzano (1781-1848). But what is this theorem saying exactly? Well, remember that if a function is continuous, it has no gaps or breaks. In other words, you can draw a graph of the function by hand without taking your pencil off the paper. Remember also that a closed interval is an interval between two points on the x axis which includes the end points. The closed interval between the points a and b on the x axis, for example, would include the points a and b, and would be denoted as [a, b]. So far so good, but what do we mean by bounded?
A function is said to be bounded if there exists both an upper and a lower limit to the values it can take. In other words, the function has both a maximum and a minimum value that it can attain. Actually, it's slightly more complicated than that. In order to understand why, we need to examine the concept of upper and lower bounds. An upper bound can be any number that is equal to or greater than the highest value that the function can take. Similarly, a lower bound can be any number that is equal to or less than the lowest value that the function can take. If the values returned by some continuous function can range from one to two, for example, then the numbers one, zero and minus one are all lower bounds of the function, and the numbers two, three and five are all upper bounds of the function.
We are specifically interested here, however, in the idea of a function having a least upper bound and a greatest lower bound. The least upper bound of a function is the upper bound that is either equal to or less than every upper bound of the function. By definition, therefore, it will also be the maximum value that the function can attain. Similarly, the greatest lower bound of a function is the lower bound that is either equal to or greater than every lower bound of the function. This number will therefore be the minimum value that the function can attain. We can express this a little more formally in terms of the function itself. Suppose we have a function ƒ(x) that is continuous for all x on the closed interval [a, b] where a ≤ x ≤ b, then ƒ(x) is bounded on [a, b] by an upper bound value yub that ƒ(x) is never greater than, and by a lower bound value ylb that ƒ(x) is never less than, for all x on [a, b].
The extreme value theorem extends the boundedness theorem. Whereas the boundedness theorem states that a continuous function defined on a closed interval must be bounded on that interval, the extreme value theorem goes further, and states that the function must attain both its maximum and minimum value, each at least once. Putting this another way, the function must attain a value equal to the least upper bound at least once, and it must also attain a value equal to the greatest lower bound at least once. Stating this slightly more formally, there must exist at least one value x = c, where c is on [a, b], such that ƒ(c) = yub. There must also exist at least one value x = d, where d is on [a, b], such that ƒ(d) = ylb. Consider the following illustration.
![The graph of the function f(x) = 3x^3 - 10x^2 defined on the closed interval [-1, 3]](images/differential_calculus_0065.gif)
The graph of the function ƒ(x) = 3x 3 - 10x 2 defined on the closed interval [-1, 3]
Here we see the graph of the polynomial function ƒ(x) = 3x 3 - 10x 2 defined on the closed interval [-1, 3]. The function attains an absolute maximum value at x = c and an absolute minimum value at x = d. The value returned by ƒ(c) will be the least upper bound of the function, and the value returned by ƒ(d) will be the greatest lower bound of the function. Note that if the function were not restricted to a finite interval, it would extend to infinity in both the positive and negative directions. If that were the case, then obviously there would be no upper or lower bounds, and no absolute extrema.
The extreme value theorem essentially guarantees that, for a continuous function defined on a closed interval, the function will always attain some absolute maximum value at least once, and will also attain some absolute minimum value at least once. Like some of the other theorems we have looked at, however, it doesn't tell us anything more specific, such as exactly where these extrema will occur, or what their actual values will be. Let's think about how we would find the absolute extrema for the function ƒ(x) = 3x 3 - 5x + 1 on the closed interval [-3, 3]. Here is the graph of the function:
![The graph of the function f(x) = 3x^3 - 5x + 1 defined on the closed interval [-3, 3]](images/differential_calculus_0066.gif)
The graph of the function ƒ(x) = 3x 3 - 5x + 1 defined on the closed interval [-3, 3]
We know that the function is continuous, since it is a polynomial function, and as such will be "well behaved". Since it is defined on a closed interval, it meets the criteria of the extreme value theorem, and will have both an absolute maximum value and an absolute minimum value. We also know that all extrema must occur at critical points. Thus each extremum in the function must occur either at a stationary point (i.e. a turning point) or at one of the end points of the interval. Looking at the illustration above, we can already see that the extrema will occur at the interval endpoints, but beyond that the graph does not give us much of a clue as to what their values will be.
The standard procedure for finding the absolute maxima and minima in this situation is to evaluate the function for all of the function's critical points. We then just need to determine which critical point has the highest value (and is thus the absolute maximum), and which critical point has the lowest value (and is thus the absolute minimum). Even though we can see that the function's two stationary points will not be absolute extrema on this occasion (although they will of course be local extrema), we will demonstrate the procedure in full. To find the function's stationary critical points (i.e. turning points), we must first find the derivative of ƒ(x) = 3x 3 - 5x + 1 by applying the appropriate rules of differentiation:
ƒ′(x) = 9x 2 - 5
Now we solve ƒ′(x) = 0 to find its roots:
9x 2 - 5 = 0
9x 2 = 5
x 2 = 5/9 = 0.556
x = ± √(0.556) = ± 0.745
Now we will evaluate ƒ(x) for each of the function's critical points (including its endpoints):
ƒ(-3) = (3)(-3) 3 - (5)(-3) + 1 = -81 + 15 + 1 = -65
ƒ(-0.745) = (3)(-0.745) 3 - (5)(-0.745) + 1 = -1.240 + 3.725 + 1 = 3.485
ƒ(0.745) = (3)(0.745) 3 - (5)(0.745) + 1 = 1.240 - 3.725 + 1 = -1.485
ƒ(3) = (3)(3) 3 - (5)(3) + 1 = 81 - 15 + 1 = 67
The function ƒ(x) = 3x 3 - 5x + 1 defined on the closed interval [-3, 3] thus has an absolute minimum at x = -3 of minus sixty-five (-65), and an absolute maximum at x = 3 of sixty-seven (67). Here once again is the graph of the function, this time with the y axis scaled down with respect to the x axis so that we can see where the curve intercepts the interval boundaries. Although we can't tell just by looking at the graph what the precise y coordinates of the absolute maximum and minimum points are, the graph does appear to correspond with the values we have calculated.
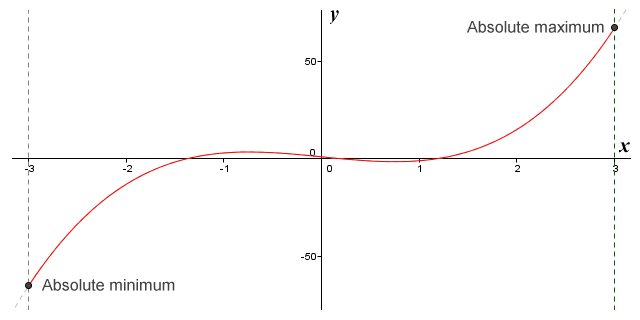
The graph of the function ƒ(x) = 3x 3 - 5x + 1 scaled to show the absolute extrema
The detailed procedure for finding the absolute extrema of a continuous function ƒ(x) defined on a closed interval [a, b] is as follows:
Let's have a look at another example. This time we will find the maximum and minimum values for the function ƒ(x) = x 4 - 3x 3 - 1 defined on the closed interval [-2, 2]. This function is also a polynomial function, so we know that it will be continuous over the interval.
First we obtain the derivative:
ƒ′(x) = 4x 3 - 9x 2
Next we solve ƒ′(x) = 0:
4x 3 - 9x 2 = 0
x 2(4x - 9) = 0
x = 0 or x = 9/4 = 2.25
Note that since x = 2.25 lies outside the interval [-2, 2], we are not interested in this particular critical point. We will however evaluate ƒ(x) for the other critical point identified (x = 0), and for the two end points of the interval:
ƒ(-2) = (-2) 4 - (3)(-2) 3 - 1 = 16 + 24 - 1 = 39
ƒ(0) = (0) 4 - (3)(0) 3 - 1 = -1
ƒ(2) = (2) 4 - (3)(2) 3 - 1 = 16 - 24 - 1 = -9
Our maximum and minimum values are therefore thirty-nine (39) and minus nine (-9) respectively. For completeness, here is the graph of the function ƒ(x) = x 4 - 3x 3 - 1. The graph of the derivative ƒ′(x) = 4x 3 - 9x 2 is shown as a dashed line. You can clearly see that the only critical point to fall within the interval [-2, 2] occurs at x = 0.
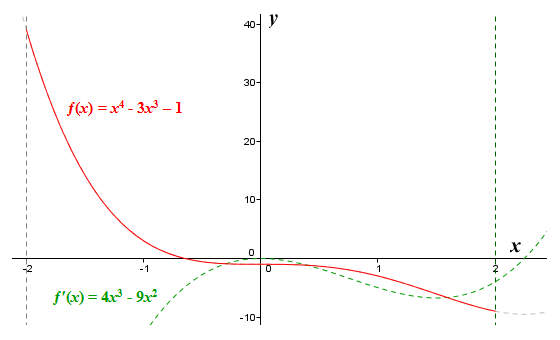
The graphs of the function ƒ(x) = x 4 - 3x 3 - 1 and its derivative ƒ′(x) = 4x 3 - 9x 2