| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Most of the differentiation problems we have studied in this section involve functions that take a single input value (the independent variable, which we usually call x) and return a single output value (the dependent variable, which we usually call y). Functions that take this form are called explicit functions. For an explicit function, the value of y is totally dependent on the value of x that we provide as the function's input. Here is a typical function of the kind you should by now be very familiar with:
ƒ(x) = x 3 - 3x + 5 (or y = x 3 - 3x + 5)
If we want to differentiate an explicit function like the one above, we can do so in a relatively straightforward manner simply by applying the appropriate rules of differentiation. Differentiating the function ƒ(x) = x 3 - 3x + 5, for example, we get:
ƒ′(x) = 3x 2 - 3 (or y′ = 3x 2 - 3)
Sometimes, however, we are faced with problems in which a function is implicit rather than explicit. This essentially means that the dependent variable is not isolated on one side of the equation. For example, consider the following very trivial example:
xy = 1
How do we differentiate y in this kind of situation? Well in this case, the answer is fairly obvious. We will simply rewrite the equation in order to isolate y on the left-hand side of the equation, and then differentiate:
y = x -1
y′ = -x -2
That of course was entirely too easy, and it certainly won't work for many of the implicit functions we come across. Nevertheless, it is always worth checking first whether the problem can be solved simply by rewriting the equation. It might save you a lot of work. Before we move on, let's just look at a slightly more meaningful (and less trivial) example of an implicit function that can be handled in this way. Consider the following equation:
x 2 + y 2 = 25
You may well have seen this equation or something very similar to it somewhere before, especially if you are familiar with the principles of coordinate geometry. It describes a circle with a radius of five (5) units, centred at the origin, as illustrated below.
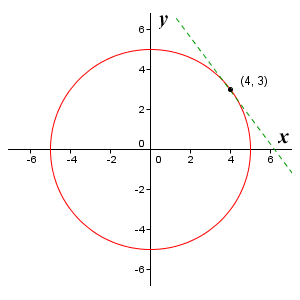
The graph of the implicit function x 2 + y 2 = 25
Note that we have identified the point (4, 3) on the circumference of the circle, and have shown the tangent to the circle at this point. Let's suppose we want to find the slope of the tangent. We could of course use our knowledge of geometry to obtain the answer, but since we are primarily interested in differentiating implicit functions, let's assume that we will be trying to do that here. In this particular case, we can rewrite the equation in order to isolate y on the left-hand side:
y 2 = 25 - x 2
y = ±√(25 - x 2)
The positive square root here represents the top half of the circle, while the negative square root represents the bottom half. To solve our particular problem, i.e. find the slope of the tangent at the point (4, 3), we are only interested in the top half of the circle, so we are only interested in finding the derivative of the function y = √(25 - x 2). Even though we have now managed to isolate y on the left-hand side of the equation, we are still faced with the problem of differentiating a compound function. In order to do so, we need to use the chain rule (if you are not familiar with the chain rule, you should probably read the relevant page covering that topic in this section).
The chain rule essentially tells us that, in order to find the derivative of the composite of two functions, we need to multiply the derivative of the outer function by the derivative of the inner function. To make life a little easier, let's rewrite the composite function so that we can invoke the power rule to differentiate the outer function:
y = (25 - x 2) 1/2
So applying the chain rule gives us:
y′ = 1/2 (25 - x 2) -1/2 (-2x)
| y′ = | -x |
| √(25 - x 2) |
And applying this to the point (4, 3) gives us:
| y′ = | -4 | = | -4 | = -1.333 |
| √(25 - 4 2) | 3 |
Unfortunately, not all implicit functions can be rewritten in this way. Sometimes it is either not possible, or simply not practical, to isolate y on the left-hand side of the equation. When that happens, we turn to a technique known as implicit differentiation in order to obtain y′. You might recall from studying the chain rule (which we mentioned above) that the essence of this rule is substitution. We use the chain rule to differentiate composite functions. A composite function actually consists of multiple nested functions. In the simplest case, two functions are involved - the outer function (i.e. the one we would normally evaluate last) and the inner function (which we would normally evaluate first). The outer function is applied to the output of the inner function.
Let's just recap how the chain rule works. Rather than attempting to differentiate the composite function as a single entity, we substitute a simple variable for the inner function and basically ignore it. We can then concentrate on differentiating just the outer function, without having to worry about the inner function. Once we have done that, we can differentiate the inner function. The next stage is to multiply the two derivatives together to get the derivative of the composite function. In the final stage, the inner function, in its original form, is substituted back into the outer function's derivative in place of the simple variable. Once you become familiar with the chain rule, it is often possible to leave out the substitution stage altogether.
We use a similar idea for implicit differentiation. In fact, you can think of implicit differentiation as a special case of the chain rule. Although we may not always be able to rewrite an implicit function in order to isolate y, we can deal with y as if it is a function of x - even if we have no idea what that function actually does. With that in mind, let's go back once more to the implicit function we saw earlier - the one that describes a circle with a radius of five units, centred at the origin:
x 2 + y 2 = 25
Remembering what we said above, we are going to treat y as if it is a function of x. We will therefore rewrite our implicit function as follows:
x 2 + y(x) 2 = 25
The important thing to note here is that the expression y(x) is not the variable y multiplied by the variable x. It represents y as a function of x. The expression y(x) 2 is therefore actually a composite function for which y(x) is the inner function, and the square function is the outer function. Suppose we now differentiate both sides of the equation. Remember that y(x) 2 is a composite function, which means we will have to apply the chain rule to it. We will therefore get the following:
2x + 2yy′ = 0
Some further explanation may be required here, since you could be forgiven at this stage for being slightly confused. You should be untroubled by how we arrived at the first term on the left-hand side of the equation. This is simply the result of applying the power rule to x 2, which gives us 2x. The zero on the right-hand side of the equation should also cause you no problems, since differentiating any constant term always results in zero. But how did we arrive at 2yy′ as the second term on the left-hand side?
Remember that y is a function of x, the exact nature of which is frankly unimportant. Differentiating y(x) 2 (the outer function) by applying the power rule gives us 2y(x), but we can ignore the (x) because it is, after all, only a placeholder to remind us that we are treating y as some function of x. In accordance with the chain rule, we now need to find the derivative of the inner function, which is simply y(x), so (again ignoring the (x)) the derivative of the inner function will simply be y′. We then multiply the two derivatives together, in accordance with the chain rule, to get 2yy′.
We now have the term y′, which is the very thing we are looking for. Consequently we can rewrite the equation to isolate y′ on the left-hand side as follows:
2yy′ = -2x
| y′ = - | 2x |
| 2y |
| y′ = - | x |
| y |
This actually gives us the derivative of the equation of the unit circle (x 2 + y 2 = 1). This means that if we were given the x and y coordinates of any point on the circumference of any circle centred at the origin, we could use this derivative to calculate the slope of the tangent to the circle at that point.
One very important thing to notice here (assuming you haven't already) is that, whereas with explicit differentiation the derivative is always expressed in terms of x (or whatever label you are using for the independent variable), that will generally not be the case for implicit differentiation. You saw above that the derivative for the equation of a circle is expressed in terms of both x and y. You will find that the derivative you obtain using implicit differentiation will almost invariably feature both the independent variable and the dependent variable.
Implicit differentiation is a process that requires a bit of practice before you feel comfortable with it, so let's try a few more examples. We'll start by differentiating the implicit function x 3 + y 3 = 4. Rewriting the function so that y becomes a function of x, we get:
x 3 + y(x) 3 = 4
Differentiating both sides of the equation gives us:
3x 2 + 3y 2y′ = 0
Solving for y′, we get:
3y 2y′ = -3x 2
| y′ = - | 3x 2 |
| 3y 2 |
| y′ = - | x 2 |
| y 2 |
Hopefully, as you get more comfortable with implicit differentiation, you will be able to solve problems of this nature without having to replace y in the implicit function with y(x). It is, after all, simply a way of reminding us that we should treat y as a function of x, and there is always the possibility that you may encounter an implicit function that incudes the term y(x) as a legitimate term! Nevertheless, keep doing it until you feel you don't need to anymore. Let's try something slightly more challenging. We'll now try to find the derivative of y = x 2y 3 + x 3y 2. Rewriting the function so that y becomes a function of x, we get:
y(x) = x 2y(x) 3 + x 3y(x) 2
Now we differentiate both sides of the equation. Remember you need to use the product rule here, as well as the chain rule. Just to remind you, the product rule states that in order to differentiate an expression that is the product of two functions, we must take the first function multiplied by the derivative of the second function, and add it to the second function multiplied by the derivative of the first function (you actually need to apply the product rule twice in this instance). Assuming you get everything right, you should end up with:
y′ = x 23y 2y′ + y 32x + x 32yy′ + y 23x 2
We'll just tidy this up a bit for the sake of good order:
y′ = 3x 2y 2y′ + 2xy 3 + 2x 3yy′ + 3x 2y 2
Now we need to solve for y′. We start by moving all the terms containing y′ over to the left-hand side:
y′ - 3x 2y 2y′ - 2x 3yy′ = 2xy 3 + 3x 2y 2
Factorising the left-hand side of the equation, we get:
y′(1 - 3x 2y 2 - 2x 3y) = 2xy 3 + 3x 2y 2
which gives us:
| y′ = | 2xy 3 + 3x 2y 2 |
| 1 - 3x 2y 2 - 2x 3y |
Let's work through one more example. This time we'll find the derivative of the implicit function y 4 + 4y - 3x 3 sin(y) = 2y + 1. Rewriting the function so that y becomes a function of x (which at some point you will probably not need to do any more) we get:
y(x) 4 + 4y(x) - 3x 3 sin (y(x)) = 2y(x) + 1
Differentiate both sides of the equation. Remember you will need to use the product rule here as well as the chain rule in order to differentiate 3x 3 sin (y). This will give us:
4y 3yʹ + 4yʹ - 3x 3 cos(y)yʹ - 9x 2 sin (y) = 2
Now we will solve for y′. First, we will rearrange the equation to get all the terms containing y′ on the left-hand side:
4y 3y′ + 4y′ - 3x 3 cos (y)y′ = 2 + 9x 2 sin (y)
Factor out y′ from the terms on the left-hand side:
y′(4y 3 + 4 - 3x 3 cos (y)) = 2 + 9x 2 sin (y)
Finally, isolate y′ on the left-hand side of the equation:
| y′ = | 2 + 9x 2 sin (y) |
| 4y 3 + 4 - 3x 3 cos (y) |
To recap, if you have an implicit function that cannot easily be rewritten as an explicit function, you can use implicit differentiation to obtain the derivative y′. The result will more often than not involve both x (the independent variable) and y (the dependent variable). The basic procedure is to take the derivative of all terms on both sides of the equation, move any terms involving y′ to the left-hand side of the equation, and move all other terms to the right-hand side of the equation. You should then be able to factor out and isolate y′ on the left-hand side. The key concept is to treat y as some function of x, which means you must differentiate any terms involving y using the chain rule, as we have seen in the examples above. Terms not involving y are differentiated in the usual way.