What Is Differential Calculus?
Differential calculus is one of the two major branches of calculus, the other being integral calculus. It is the process of finding the instantaneous rate of change of some quantity that varies in a non-linear way. Both linear and non-linear behaviours can be described using mathematical functions. These functions tell us how one quantity (the dependent variable or output) varies in response to changes in another quantity (the independent variable or input). We apply differential calculus primarily to the study of non-linear behaviours. Functions that describe such behaviours are said to be non-linear functions.
Plotting the graph of a non-linear function produces a curve that enables us to visualise the relationship between the input variable (x) and its corresponding output variable (y). The slope of the graph will vary continuously, and the slope at a single point on the graph represents the rate at which y is changing at that point in relation to x. The numerical value that we obtain for the slope is called a derivative. The process of finding the derivative is called differentiation.
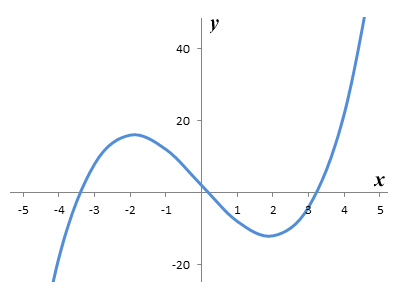
The graph of the non-linear function ƒ(x) = x3 - 11x + 2
The slope of a single point on a curve is the slope of the tangent to the curve at that point. A tangent is a straight line that touches a curve at a single point without intersecting it. The derivative of a function for some value of x is the slope of the tangent to the graph of the function at that point. It is also sometimes expressed as the linear function that describes the tangent line. The illustration below shows the graph of the non-linear function ƒ(x) = x2 - 4x + 2, together with the tangent to the graph at point P (x = 3). We can think of the linear function that describes the tangent line as a linear approximation of the non-linear function at point P.
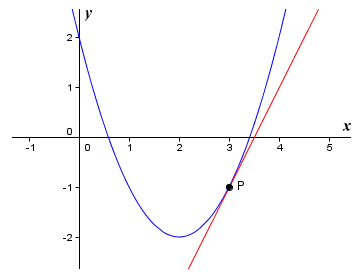
The graph of ƒ(x) = x2 - 4x + 2 and the tangent to point P (x=3)
We know that the graph of a linear function is always a straight line. All we need in order to find the slope of a straight line are the x and y coordinates of any two points on the line. We can then apply the standard formula for the slope of a straight line to obtain the slope. The graph of a non-linear function, on the other hand, is always a curve. Finding the slope of a curve at a single point on the curve is somewhat more difficult to do, since there is no simple formula we can use for this purpose. This is the problem that differential calculus was developed to solve.
