| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Luminous intensity is one of the seven base quantities defined by the International System of Units, and is essentially a measure of how much light is emitted in a given direction by a light source. It is also a photometric unit, which means we are measuring visible light, using parameters determined according to human perceptions. This page will look at a range of photometric values, how they are measured, and how they relate to one another.
Photometry is a branch of science concerned with the measurement of the brightness of light from a human perspective, i.e. visible light. It should not be confused with radiometry, another branch of science concerned with the measurement of all electromagnetic radiation (including visible light). Photometry essentially measures the brightness of different wavelengths of visible light according to how sensitive the human eye is to each wavelength.
Luminous intensity is one of the seven base units defined by the International System of Units. It is a measure of the wavelength-weighted power emitted by a light source, in a particular direction and at a specific frequency, per unit solid angle (we will enlarge upon this description later).
The reference frequency used is 540 × 10 12 hertz, which corresponds to a wavelength of approximately five hundred and fifty-five nanometres (555 nm), and puts it right in the middle of the visible light spectrum. Light at this frequency and wavelength is generally accepted to be that to which the human eye is most sensitive. The SI unit of luminous intensity is the candela (cd), which is formally defined as:
"the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 × 10 12 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian"
The main source of visible light on Earth is the Sun. Approximately forty-four percent of the solar radiation reaching the Earth's surface is made up of visible light. By comparison, only about ten percent of the energy emitted by a candle can be seen as visible light. The rest is emitted as thermal energy (infrared radiation). Sunlight is important because it provides the energy needed for photosynthesis - the chemical process that produces sugars (in the form of starches) in green plants. These sugars are consumed by other living organisms when they eat the plants, and provide almost all of the energy used by all living organisms.
When we talk about visible light, we are usually referring to light that can be detected by the human eye, because this "visible light" is what allows us to see. Estimates of the range of wavelengths we can see vary, but the lower end of the range is around four hundred nanometres (400 nm) which corresponds to a frequency of about seven hundred and fifty terahertz (750 × 10 12 Hz). The upper end of the range is around seven hundred nanometres (700 nm), corresponding to a frequency of about four hundred and thirty terahertz (430 × 10 12 Hz).
Wavelengths from four hundred nanometres down to about ten nanometres (10 nm) belong to the ultra violet part of the electromagnetic (EM) spectrum. These wavelengths cannot be detected by the photoreceptors (known as rods and cones) in the light-sensitive part of the human eye (the retina), because they are absorbed by the transparent front part of the eye (the cornea) and the eye's internal lens. If too much ultra violet light is absorbed, it can damage the eye and even cause blindness.
Wavelengths of between four hundred and seven hundred nanometres are detected by the human eye because they pass through the cornea and lens, and have sufficient energy to cause tiny chemical changes in the light-sensitive rods and cones of the retina. These chemical changes stimulate the production of nerve impulses, which are sent to the brain's visual cortex via the optic nerve.
Wavelengths from seven hundred nanometres up to about one millimetre (1 mm) belong to the infrared part of the EM spectrum. Some infrared wavelengths are absorbed by the cornea and internal lens. Other infrared wavelengths actually reach the retina, but do not have sufficient energy to cause the kind of chemical changes in the retina that would trigger nerve impulses.
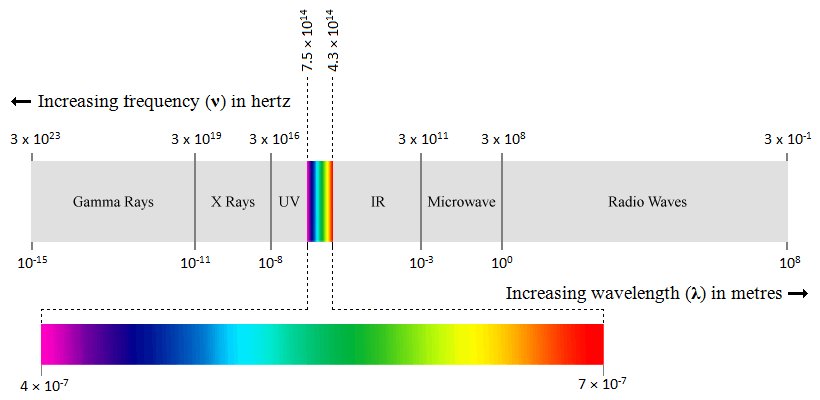
Visible light is only a small part of the electromagnetic spectrum
Many heat sources emit both infrared radiation and visible light. The peak wavelengths of these thermal emissions become shorter as temperature increases. You can see the effect as a piece of metal is slowly heated up. At first, only thermal (infrared) radiation is emitted. As the metal gets hotter, the peak wavelengths move into the visible part of the electromagnetic spectrum, and a faint red glow can be seen.
As the temperature of the metal increases further, the glow becomes brighter and brighter, until it is almost white. At very high temperatures it may even become blue-white, as the peak wavelengths start to move into the ultra violet part of the electromagnetic spectrum.
At first, apart from the moon and stars, our ancestors had no other source of light during the hours of darkness. Eventually man learned to make fire and invented various forms of artificial lighting, including pitch-burning torches, candles made from wax or animal fat, and oil-burning lamps.
Today, we rely on the generation of electrical power to provide lighting in our homes and places of work. Most forms of transportation generate their own electrical power to provide lighting for navigation, and for the convenience of their passengers. Even bicycles can generate their own light, if equipped with a dynamo. And of course, to guard against power failures, most of us own at least one or two battery-powered flashlights and a stock of candles!
Photometry uses many different units to measure brightness because of the diverse nature of the light sources themselves. Some light sources emit light in all directions simultaneously (like a light bulb), while some focus all of their light in a single direction (like a flashlight).
Other light sources can only be seen against a dark background. The perception of brightness also changes with distance, because light spreads out as it travels away from a light source. And of course, light is reflected by different surfaces to varying degrees, and in different directions, depending on the nature of the surface and the angle at which the light strikes it.
Photometry, then, is a fairly complex business, and the number of different units used to measure photometric quantities is a reflection of that complexity. The table below lists the main photometric quantities and units used to measure brightness, and gives a brief description of each. Note that some photometric quantities have the suffix "v". This is to avoid confusion with radiometric quantities.
| Quantity | Symbol | Unit | Unit Symbol | Description |
|---|---|---|---|---|
| Luminous intensity | Iv | candela (lm/sr) | cd | Luminous power per unit solid angle |
| Luminous flux | Φv | lumen (cd·sr) | lm | Luminous energy per unit time - the product of luminous intensity and steradians |
| Luminous energy | Qv | lumen second | lm·s | Energy emitted as light - the product of luminous flux and its duration |
| Luminance | Lv | candela per square meter | cd/m 2 | Luminous power per unit solid angle per unit projected source area |
| Illuminance | Ev | lux (lm/m 2) | lx | Luminous power incident on a surface in lumens per square metre |
| Luminous exitance | Mv | lux (lm/m 2) | lx | Luminous power emitted from a surface in lumens per square metre |
| Luminous exposure | Hv | lux second | lx·s | The product of illuminance and its duration |
| Luminous energy density | ωv | lumen second per cubic metre | lm·s·m -3 | Luminous energy per cubic metre |
| Luminous efficacy | η | lumen per watt | lm/W | Ratio of luminous flux to radiant flux or power consumption, depending on context |
| Luminous efficiency | V | - | - | Luminous efficacy expressed as a fraction of the maximum possible luminous efficacy - a dimensionless quantity, usually expressed as a percentage |
The average sensitivity of the human eye to different wavelengths of visible light can be modelled using one of the luminosity (or luminous efficiency) functions in common use. Different functions are used, depending on the prevailing conditions, because the eye will respond differently to a particular wavelength depending on how light or dark it is.
In daylight, or when sufficient artificial light is provided, our vision is said to be photopic. Photopic vision allows us to see things clearly, and to process the visual information we receive reasonably quickly. It also allows us to see colours. In darkness or very low light conditions, our vision becomes scotopic. This means that we lose our clarity of vision, and it takes significantly longer to process visual information. We also lose the ability to see colours.
There is also a third type of vision called mesopic vision which combines elements of photopic and scotopic vision. We typically use this third form of vision when it is not quite dark, or when (for example) we have to rely on street lighting.
Although photometry is typically based on the eye's response to a light source in well-lit conditions (i.e. the photopic response), a number of different luminosity functions have been used. One reason for this is that, as we have said, the eye's response to different wavelengths will vary, depending on the lighting conditions under which it is evaluated. Another reason is the fact that such measurements are based on subjective judgements as to which of a pair of different coloured lights is brighter in order to determine the relative sensitivity of the human eye to different wavelengths.
To clarify, we are not using instruments here to measure the radiance of a light source (i.e. its actual radiant power). A luminous efficiency function describes the average spectral sensitivity of human of human visual perception of brightness - in other words, it is a measure of how bright the "average" human being perceives light at a particular wavelength to be. It is based on an interpretation of the responses obtained from human test subjects over many decades, and the research is ongoing.
Various standard luminous efficiency functions have been published by the International Commission on Illumination (CIE) or Commission internationale de l'éclairage, to give it its French title. This organisation, based in Vienna, is the international authority on light, illumination, colour and colour spaces.
We will only consider two luminous efficiency functions for the purposes of this discussion - the photopic luminous efficiency function, which best approximates the response of the human eye in daylight, and the scotopic luminous efficiency function, which reflects the changes in the response of the human eye when light levels are low.
In well-lit conditions, the sensitivity of the human eye to visble light at different wavelengths is best represented by the photopic luminosity function. The original luminous efficiency function V(λ) was proposed by K.S. Gibson & E.P.T Tyndall of the US National Bureau of Standards in 1923, and adopted by the CIE in 1924.
The function models the ratio of the energy of a light source of the wavelength to which the eye is most sensitive (λmax ) to the energy of a light source of wavelength λ that produces the same response in the test subject. The function was based on test data obtained by a number of different laboratories, and using a number of different methods.
Various revisions to the V(λ) function have been implemented. The first change occurred in 1951 following a proposal by the American physicist D.B. Judd. A further revision was proposed by J. J. Vos of the Instituut voor Zintuigfysiologie (Institute for Sense Physiology) in the Netherlands in an attempt to correct some minor anomalies introduced by Judd's proposal. The result is known as the Judd-Vos modified CIE V(λ), and the curve produced is illustrated below.
A new luminous efficiency function, V2*(λ), was proposed in 2005 by Lindsay T. Sharpe and Andrew Stockman of University College London, and Wolfgang Jagla, and Herbert Jägle of Eberhard-Karls-University, Germany. The authors claim that the new function improves upon the original CIE 1924 V(λ) function and its subsequent modifications.
![CIE Photopic V(λ) modified by Judd (1951) and Vos (1978) [also known as CIE VM(λ)]](images/measurement_0096.gif)
CIE Photopic V(λ) modified by Judd (1951) and Vos (1978) [also known as CIE VM (λ)]
Source: Colour and Vision Research Laboratory, University College London
Testing is carried out on what are known as "standard observers". Typically, the test subject - a person considered to have normal vision - is asked to compare the brightness of a monochromatic light source at a reference wavelength of five hundred and fifty-five nanometres (the wavelength to which the eye has the greatest sensitivity) with the brightness of a second monochromatic light source having a different wavelength.
The reference wavelength (555 nm) is given a normalised luminous efficiency value of 1.0. Initially, even though both light sources will have the same radiant intensity, the reference wavelength will appear to be brighter because the eye is more sensitive to it. Its brightness is gradually reduced until the test subject indicates that they consider both light sources to be at the same level of brightness. The fraction by which the brightness of the reference wavelength has been reduced is then subtracted from 1.0 to obtain the luminous efficiency value of the second wavelength. For wavelengths at either end of the visible spectrum, this value will tend to zero.
In order to obtain meaningful results, a large number of "standard observers" must be tested over the entire range of visible wavelengths. The results for each wavelength are averaged in order to obtain the eye's relative sensitivity to that wavelength, and a luminous efficiency curve like the one illustrated above is derived (this curve is sometimes called a V-lambda curve).
In low-light conditions, the sensitivity of the human eye to visble light at different wavelengths changes, and is best represented by the scotopic luminosity function. This is because of the way the rods and cones in the retina of the eye work. The cones are used mostly for daytime vision. They are not particularly sensitive to changes in light levels, but can discern between red, blue and green wavelengths.
Rods play the predominant role in night time vision. They are much more sensitive to light than cones (and far more numerous), but are much less sensitive to colour. They have their peak sensitivity in the blue part of the visible light spectrum at five hundred and seven nanometres (507 nm), and are not particularly sensitive to red light. As a consequence, the scotopic luminous efficiency curve is shifted towards the blue end of the spectrum. The standard scotopic luminosity function V′(λ) was adopted by the CIE in 1951, based on measurements obtained by US scientists George Wald and B.H Crawford, is illustrated below.
The scotopic luminous efficiency curve was established in much the same way as the photopic curve, by testing a large number of subjects over the entire range of visible wavelengths and averaging the results for each wavelength. The only difference is that the reference wavelength is set to five hundred and seven nanometres (507 nm).
Luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle. To fully understand this definition, it may be necessary to break it down a little. We should probably start by saying that luminous intensity is not the same thing as radiant intensity, although the two concepts are closely related.
Radiant intensity is measured in terms of the total radiant power emitted per unit solid angle from a point source, across the entire electromagnetic spectrum. Luminous intensity only applies to the visible part of the electromagnetic spectrum, and is the perceived power per unit solid angle.
Our perception of brightness for a given wavelength will depend on the sensitivity of the eye to that wavelength. As we saw above, the eye's sensitivity to visible light peaks at a wavelength of five hundred and fifty-five nanometres, and can be modelled using the luminosity (or luminous efficiency) function. This is what we mean when we talk about wavelength-weighted power.
The other thing that may require some further explanation is what we mean when we talk about a unit solid angle (if you are reasonably well acquainted with three-dimensional geometry you are probably already familiar with this concept). In two-dimensional geometry, we often talk about radians. A radian is the angle subtended at the centre of a circle by an arc on the circumference of the circle that has the same length as the radius of the circle. This principle is illustrated below.
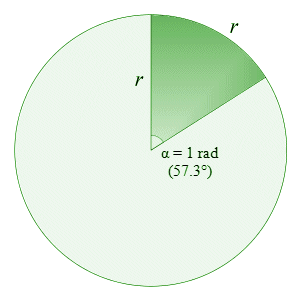
An arc of length r subtends an angle of 1 radian (57.3°)
Now imagine a sphere of radius r. Let's suppose we have a portion of the sphere that is cut off by a plane (this is known as a spherical cap or spherical dome), and that has a surface area of r 2. If we draw a line from every point on the perimeter of this area to the centre of the sphere, we will have a spherical sector. A spherical cap with an area of r 2 subtends a solid angle (you can think of this as a three-dimensional angle) of one steradian at the centre of the sphere. The principle is illustrated below.
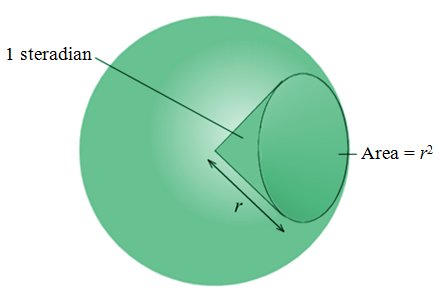
A spherical cap with an area of r 2 subtends a solid angle of 1 steradian
In the context of the power emitted by a light source, you can think of a steradian as a cone of light spreading out from a point at the centre of a sphere with a radius of one metre. The light would illuminate an area of one square metre on the inner surface of the sphere.
The unit of luminous intensity is the candela (cd), an SI base unit. Before the candela came into being, a number of different units were used for luminous intensity, most of which were based on the brightness of a "standard" candle flame (a common candle emits light with an average luminous intensity of approximately one candela). One problem with this was the fact that the specification used for a "standard" candle varied from one country to the next. In fact, some countries used oil-burning lamps instead of candles, so overall there was little consistency.
Things moved forward a little in 1909, when the USA, France and Great Britain adopted a unit called the international candle based on the output of a specific type of incandescent carbon filament lamp, but this standard was not adopted in other parts of the world, and it soon became apparent that a standard based on incandescent lamps was only going to be a temporary solution. A much more rigorously-defined unit was needed.
During the early 1930s, the ideal solution appeared to present itself in the form of a Planckian radiator. A Planckian radiator is an ideal blackbody radiator (a material that absorbs and emits radiant energy). It obeys Planck's radiation law, which is named after the German theoretical physicist Max Karl Ernst Ludwig Planck (1858-1947).
A Planckian radiator not only absorbs all incident radiation but also emits radiation at all wavelengths, with a spectral power distribution that depends only on wavelength and temperature. In other words, if we have an ideal Planckian radiator at a known temperature, we can predict the power of the emitted radiation for a given wavelength.
In 1939, the Consultative Committee for Photometry put forward a proposal to the International Committee for Weights and Measures (CIPM) for a new definition of the unit of luminous intensity. The redefined unit was to be called the "new candle", and was based on the luminous intensity of a Planckian radiator at the temperature of freezing platinum - two thousand and forty-five kelvins (2045 k). Proceedings were interrupted by the Second World War, but by 1946, the definition of the "new candle" had been more or less agreed upon and was as follows:
"The value of the new candle is such that the brightness of the full radiator at the temperature of solidification of platinum is 60 new candles per square centimetre."
The new unit was adopted by the CIPM at the 9th General conference on Weights and Measures (CGPM) in 1948. In 1967, the 13th CGPM decided to drop the name "new candle" in favour of "candela" (the Latin word for candle) and amended the definition of the candela by specifying that the solidifying platinum was subject to a pressure of 101 325 pascals or 101 325 newtons per square metre (in other words, standard atmospheric pressure). The revised definition was thus:
"The candela is the luminous intensity, in the perpendicular direction, of a surface of 1 / 600 000 square metre of a black body at the temperature of freezing platinum under a pressure of 101 325 newtons per square metre."
The new definition would be short-lived, however. It turned out to be rather more difficult to set up a Planck radiator with the required specifications under laboratory conditions than envisaged, not least because of the high temperatures involved. Furthermore, advances in radiometry meant that new techniques were becoming available for measuring electromagnetic radiation, including the measurement of the radiant intensity of visible light.
The 16th General conference on Weights and Measures (CGPM) in 1979 adopted the definition of the candela that we saw at the beginning of this page, and which we reproduce here:
"the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 10 12 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian"
The seemingly arbitrary choice of the fraction 1/683 was made in order to ensure that the new definition of the candela would give it the same value as the old definition. The frequency chosen for the monochromatic light source corresponds to a wavelength of five hundred and fifty-five nanometres (555 nm), which as we have seen is the wavelength to which the eye is most sensitive.
Perhaps the most important aspect of this redefinition of the candela is that it enables us to derive the following formula for determining the luminous intensity of monochromatic light of a particular wavelength:
Iv = 683 × V(λ) × Ie
where:
Iv is the luminous intensity in candela (cd)
Ie is the radiant intensity in watts per steradian (W/sr)
V(λ) is the standard luminosity function
In most cases, of course, the light source we want to measure will be polychromatic (i.e. it will contain radiation of more than one wavelength). That being the case, it is necessary to sum, or integrate, over the spectrum of wavelengths present in order to obtain the luminous intensity of the light source. We can modify the formula to reflect this as follows:
| Iv = 683 | ∫ | ∞ | V(λ) | dIe (λ) | dλ |
| 0 | dλ |
We now have a means by which we can use modern radiometric techniques to measure the radiant intensity of a light source and derive from it the luminous intensity of the light source. The purpose of the luminosity efficiency function V(λ) in these formulae is to assign a weighting to the radiant intensity of each wavelength measured according to the average sensitivity of the human eye to that wavelength.
Another point worth mentioning, and one that may have occurred to you, is that if we use a sensor of some kind to measure the radiant intensity of a light source, the value of the readings obtained will depend on how far away the sensor is from the light source, because the light spreads out as it moves away from the source. This is not a problem, however, because we use a sensor with a receiving area of a known size to measure the light received.
Whatever the distance is between the sensor and the light source (in metres), one steradian will be the square of that distance. Let's say we have a sensor with a receiving area of one square centimetre, and that it is exactly one metre from the light source. A steradian in this case will be one square metre. The area of our sensor is one square centimetre, which is one ten thousandth of a square metre (i.e. one ten thousandth of a steradian). We therefore multiply the measured radiant intensity by ten thousand in order to get the radiant intensity per steradian.
Luminous flux or luminous power is a measure of the perceived power of the light radiated in all directions by a light source per unit time. Luminous flux is not the same thing as radiant flux, although the two concepts are closely related. Radiant flux is a measure of the total power of the electromagnetic radiation emitted from a source at all wavelengths, whereas luminous flux is a measure of the electromagnetic radiation emitted at only those wavelengths falling within the visible part of the electromagnetic spectrum, weighted according to the average sensitivity of the human eye to each wavelength.
The SI unit of luminous flux is the lumen (lm). One lumen is defined as the luminous flux emitted into one unit solid angle (i.e. one steradian) by an isotropic light source with a luminous intensity of one candela (an isotropic light source is one that emits light in all directions at the same intensity). Luminous flux is thus the product of luminous intensity and steradians (cd·sr).
Consider an isotropic light source with a luminous intensity of one candela. We know that one steradian is the solid angle subtended by an area on the surface of a sphere equal to the square of the sphere's radius (r 2). We also know that the total surface area of a sphere is four times pi times the radius of the sphere squared (4πr 2). The total solid angle subtended by a sphere is thus π steradians. The total luminous flux (Φv ) produced by our light source is therefore given by:
Φv = 4π lm ≈ 12.57 lm
The luminous flux of a light source in lumens is a measure of its total light output, whereas luminous intensity is a measure of how bright the light appears to be in a particular direction. To illustrate this, consider a flashlight with a total luminous flux of two hundred lumens (200 lm) that produces a cone of light with a solid angle of one-tenth of a steradian (0.1 sr). We would calculate the luminous intensity of our flashlight beam as follows:
Iv = 200 lm ÷ 0.1 sr = 2000 cd
Now let's consider an isotropic light source with the same total luminous flux (two hundred lumens). As we have seen, an isotropic light source covers a solid angle of 4π steradians, so the luminous intensity (in any direction) of our isotropic light source would be calculated as follows:
Iv = 200 lm ÷ 4π sr = 15.915 cd
The light from a flashlight will usually appear much brighter than the light from an incandescent light bulb, even though the total luminous flux produced by the flashlight may actually be far less less than the total luminous flux produced by the light bulb. This is because the light from the flashlight is concentrated into a narrow beam, whereas the light bulb can be considered to be an isotropic light source because it emits light in (almost) all directions.

A flashlight beam appears many times brighter than the light from an incandescent light bulb
A mains-powered seventy-five watt (75 W) incandescent bulb, for example, produces about eleven hundred lumens (1100 lm) and has a luminous intensity of approximately eighty-five candela (85 cd). By comparison (according to its manufacturers), a Mini MAGLITE LED flashlight that runs on two AAA batteries produces one hundred and eleven lumens (111 lm) and has a peak beam intensity of two thousand seven hundred and twelve candela (2712 cd). Putting this into context, the flashlight produces one tenth the luminous flux of the incandescent bulb, but is more than thirty times as bright.
The radiant flux produced by a light source is a physical quantity that can be objectively measured using appropriate equipment and techniques. The luminous flux of the light source, as we have said, is the perceived power of the light source. The luminous efficacy (symbol: η) of a light source is the ratio of luminous flux to either radiant flux or power consumption, depending on context, and is expressed in lumens per watt (lm/W).
The luminous efficacy of a modern light bulb is usually given in terms of its power consumption. If we want to find the luminous flux of a light bulb, we can use the following formula to convert watts to lumens:
Φv = P × η
where:
Φv is the luminous flux in lumens (lm)
P is the power consumption in watts (W)
η is the luminous efficacy of the bulb in lumens per watt (lm/W)
These days, the luminous flux and power rating for a commercially available light bulb is invariably stated on the packaging, as well as being published in the manufacturer's data sheet, so doing this kind of calculation is not usually necessary. The manufacturer will have carried out extensive testing of their products to ascertain this kind of data before putting them on the market.
Nevertheless, physicists will sometimes be faced with the need to measure the radiant flux of a light source and calculate its corresponding luminous flux. This brings us back to luminous efficiency - a dimensionless quantity that expresses the luminous efficacy of a light source as a fraction of the maximum possible luminous efficacy for that light source.
Under photopic conditions, the visible wavelength that produces the maximum possible luminous flux is five hundred and fifty-five nanometres (555 nm), because this is the wavelength to which the eye is most sensitive. At this wavelength, the luminous flux will be six hundred and eighty-three lumens per watt (683 lm/W). By definition, this value is also the maximimum possible efficacy of a light source, and is assigned a luminous efficiency of one (1.0).
Under scotopic conditions, the eye is most sensitive to light at a wavelength of five hundred and seven nanometres (507 nm). The rods in the retina, which are responsible for night time vision, are both far more numerous and far more sensitive to light than cones. Consequently, the luminous efficacy of monochromatic light at this frequency reaches a maximum value of seventeen hundred lumens per watt (1700 lm/W).
Remember that luminous flux is the perceived power of a light source. It is dependent on the sensitivity of the eye to the entire spectrum of visible wavelengths emitted by the source, and the radiant flux (or radiant power) produced at each wavelength. We weight the radiant flux at each wavelength using the luminosity function V-lambda. The total luminous flux of a light source is thus the weighted sum of the power of all of the visible wavelengths present.
The formula for the luminous flux of a monochromatic light source is as follows:
Φv = Φe × V(λ) × 683 lm/W
where:
Φv is the luminous flux in lumens (lm)
Φe is the radiant flux in watts (W)
V(λ) is the luminous efficiency function
Finding the luminous flux for a polychromatic light source is somewhat more difficult, because we need to establish the spectral power distribution for the source (i.e. the radiant power of each visible wavelength present). The total luminous flux for the source is then the sum of the luminous flux of all of the visible wavelengths.
Illuminance is defined as the total luminous flux incident on a surface in lumens per square metre (lm/m 2). It is a measure of how well the incident light illuminates the surface. The SI unit of illuminance is the lux (symbol: lx). Illuminance was in the past called "brightness", but the term was abandoned because it tended to also be used as a synonym for luminance, which is not the same thing.
A concept closely related to illuminance is that of luminous exposure - the amount of luminous flux per square metre incident on a surface over a given period of time. Luminous exposure is the product of Illuminance and the duration of the time period in seconds.
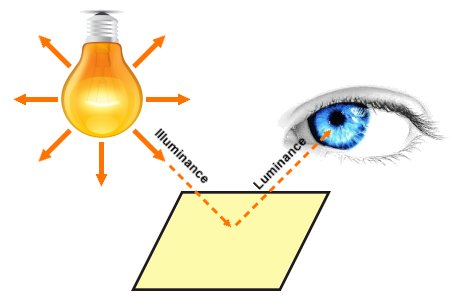
Illuminance illuminates an object or surface; luminance is what the eye sees
The amount of illuminance falling on a surface due to an isotropic light source depends on three things. It is directly proportional to the intensity of the light source. It is also dependent upon the distance between the light source and the surface being illuminated, because the light spreads out as it moves away from the source. Finally, it is dependent upon the angle at which the light is incident upon the surface.
In 1760, the Swiss polymath Johann Heinrich Lambert (1728-1777) published his book Photometria, in which he accurately described a number of photometric principles and identified a number of important photometric quantities. Lambert's work was a landmark in the field of photometry because it was the first text to describe photometric quantities and the relationships between them in mathematical terms. In essence, Lambert's work brought clarity to a subject that had previously been only poorly understood.
Lambert defined two important laws relating to Illuminance. The first of these laws is known as the inverse square law. It states that the illumination on a surface due to a point light source is inversely proportional to the square of the distance between the light source and the surface. The second is Lambert's cosine law, which states that the illumination on a surface varies as the cosine of the angle of incidence. Using a combination of these laws, we can express the illuminance Ev at a point on a surface as follows:
| Ev = | Iv cos(θ) |
| d 2 |
where:
Ev is the illuminance in lux (lx)
Iv is the luminous intensity of the light source in candela (cd)
θ is the angle of incidence (the angle angle between the light and the normal to the illuminated surface)
d is the distance from the light source to the target point in metres (m)
We stated above that illuminance is the total luminous flux incident on a surface in lumens per square metre. Since one candela represents one lumen per steradian, we can also express the illuminance Ev at a point on a surface as:
| Ev = | Φv cos(θ) |
| 4πd 2 |
where:
Φv is the luminous flux in lumens (lm)
Note that the above formulae only really apply if the light source can be considered to be a point source. For an extended light source, the calculations required are somewhat more involved, and are beyond the scope of this discussion.
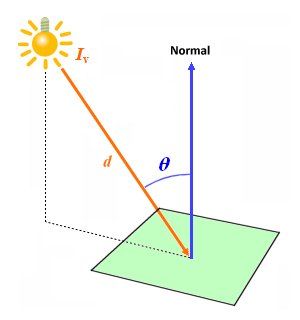
Illuminance Ev depends on the luminous intensity Iv of the source, the distance d from the source, and the angle of incidence θ
The amount of illuminance Ev (in lux) falling on a given area can be calculated as the quotient of the luminous flux Φv (in lumens) incident on the area in question and the size of the area (in square metres):
| Ev = | Φv |
| Area |
The tricky part here is to work out just how much luminous flux is actually falling on the specified area. We often come across exam questions that require the calculation of the illuminance falling on a surface. The question usually gives the luminous intensity of the light source and the distance to the surface. For example:
"A seventy-five candela point source of light is two and a half metres away from a painting. What is the illumination on the painting in lux?"
Unless otherwise specified, you are usually required to calculate the illuminance for the point on the target surface nearest to the light source. Unless the question specifically states otherwise, you should assume the angle of incidence to be zero. Note that the way in which you are expected to formulate your answer may vary, depending on who sets the exam - you might for example see a model solution to the above problem written something like this:
Φv = 4π × 75 cd = 300π lm
| Ev = | Φv | = | 300 π lm | = 12 lx |
| 4πr 2 | 4π(2.5 m) 2 |
To recap, here are the two standard formulae you should be aware of in this respect:
| (1) Illuminance = | luminous flux × cosine (angle of incidence) |
| 4π × distance 2 |
| (1) Illuminance = | luminous intensity × cosine (angle of incidence) |
| distance 2 |
These formulae both give the same result, which is the illuminance measured in lumens per square metre at a point that is at a given distance from an isotropic (point) light source and at a specified angle of incidence.
Calculating the average Illuminance from an isotropic light source falling on a planar surface is only possible if we know the total amount of luminous flux falling on that surface. Since both the angle of incidence and the distance from the light source will vary continuously over the planar surface, this value is far more difficult to calculate.
Let's look at another example. Supposing we want to calculate the illuminance falling on a desk from a 100W incandescent ligh bulb producing 1700 lumens, suspended two metres above the exact centre of the desk. To avoid making things overly complicated, we will consider the light bulb to be an isotropic point light source. The illuminance Ev falling on a point at the centre of our desk is given by:
| Ev = | Φv cos(θ) |
| 4πd 2 |
We can ignore the cosine term for the moment, since the light source is directly over the centre of the desk, which means that the angle of incidence is zero degrees. So, for our incandescent light bulb, the Illuminance falling on a point at the centre of the desk is:
| Ev = | 1700 | = 33.820 lx |
| 4π × 4 |
Only the very centre of the desk is exactly two metres from the light source. All other points on the surface of the desk are further away, and the light from the source is incident on these points at different angles. For example, using basic geometry and trigonometry, we can determine that each corner of the desk is 2.29 metres away from the light source, and that the light incident on each corner will make an angle with the normal of 35.13 degrees. Substituting these values into our illuminance formula, we get:
| Ev = | 1700 × cos(35.13°) | = 21.098 lx |
| 4π × (2.29) 2 |
To understand why the angle of incidence makes such a difference, we need to consider what happens when a parallel beam of light from an extended source falls on a planar surface. Light from the Sun, for example, can be considered to illuminate a flat surface uniformly, because the Sun is so far distant that light rays from the Sun striking the surface can be considered to be parallel.
Imagine a parallel beam of light with a rectangular cross section travelling through space in a given direction. We can measure the luminous flux per unit area (known as the luminous flux density) of this beam of light at any point along its length and get the same result, because the beam is parallel - it neither converges nor diverges. What will happen if the beam is incident on a planar surface at an angle? The diagram below illustrates the concept.
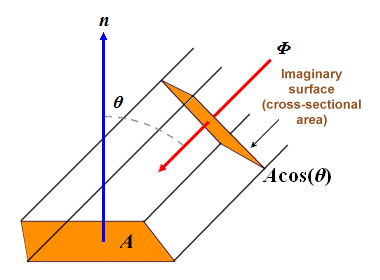
A parallel beam of light incident on a planar surface
Area A is the area illuminated by the beam. The size of area A, and consequently the amount of luminous flux per unit area falling on area A, will depend on the angle of incidence θ. If the size of the angle increases, so does the size of the illuminated area.
The illuminance E falling on an imaginary surface consisting of the cross-sectional area of the beam at any point along its length is equivalent to the luminous flux density of the parallel beam of light, which is equal to the luminous flux Φ (in lumens) divided by the cross-sectional area of the beam Acos(θ) (in square metres):
| E = | Φ |
| Acos(θ) |
Since the same amount of luminous flux falls on surface A, the illuminance Eθ on A is given by:
| Eθ = | Φ |
| A |
And therefore:
Eθ = Ecos(θ)
Luminance is defined as luminous power per unit solid angle per unit projected source area. In other words, it is the luminous intensity per unit area passing through, emitted from, or reflected by an object or surface in a given direction. The SI unit of luminance is the candela per square metre (cd/m 2), sometimes called a nit.
A concept closely related to that of luminance is luminous exitance (also known as luminous emittance), which is the total luminous flux per unit area emitted from a surface in lumens per square metre, and which, like illuminance, has the lux as its unit.
Luminance is often used to characterise the light emitted or reflected by a flat, diffuse surface. A diffuse surface is one that reflects the light incident on it in many directions (unlike a mirror, which reflects light in only one direction). A surface that is perfectly diffuse and reflects the light incident upon it evenly in every direction is sometimes called a Lambertian surface, after Johann Lambert (see above), who first described such a surface in his book Photometria.
Luminance is also often used to characterise the brightness of display screens. A typical computer screen, for example, has a luminance of between fifty and three hundred candela per square metre. Laptops and personal computers, tablets, e-books and mobile telephones tend to have screens with a diffuse surface because it helps to disperse ambient light rather than reflecting it back towards the user. Such screens are often described as "anti-glare" screens.
The luminance emitted by a surface will determine how bright the surface appears to an observer. In fact, when we look at an object, what we are actually seeing is the object's luminance. Exposure to too much luminance, even for a short time, can permanently damage your eyesight due to local heating of the retina, which is why (for example) you should never look directly at the Sun without using some kind of protective eyewear. The Sun at midday has a luminance of around one-point-six billion candela per square metre (1.6 × 10 9 cd/m 2)!
The degree to which a surface reflects electromagnetic radiation (including, of course, visible light) is called reflectance, defined as the ratio of the reflected radiant flux to the incident radiant flux. The degree to which a surface reflects visible light is sometimes called its light reflectance value (LRV). For the purposes of this discussion, we will refer to it simply as reflectance (Rv ). A dark surface that completely absorbs the light incident upon it has a reflectance of zero. A white surface that reflects all all of the light has a reflection factor of one.
You can get an instinctive feel for how luminance works by using a blank sheet of matt white paper. The paper will generally behave like an ideal diffuse reflecting surface (except when viewed from a very oblique angle), and will scatter incident light equally in all directions. Place the paper in a location where it will be uniformly illuminated, and then move around the room in order to view the paper from different angles, and from different distances. You should find that the amount of light being reflected by the paper does not appear to change.
Given what we know about the way in which both distance and the angle of incidence affect the degree to which a light source illuminates a surface, you may well wonder how it is possible that the apparent brightness of an illuminated surface (i.e. its luminance) does not appear to change significantly, regardless of the viewing angle or the distance between the surface and the observer. Let's deal with the question of distance first.
Suppose we imagine each point on the surface of the paper to be a point light source. According to the inverse square law, the luminous flux density of the light emanating from this source will be inversely proportional to the square of the distance between the source and the observer. The size of the image projected onto the retina of the eye, however, will also be inversely proportional to the square of the distance between the source and the observer. This effectively cancels out the effect of the inverse square law as it relates to luminous flux density, so that we perceive the luminance of the surface as being constant regardless of distance.
A similar situation exists with respect to the viewing angle. Like illuminance, luminance is subject to Lambert's cosine law. This law, as it applies to luminance, states that the luminous intensity in a given direction, radiated or reflected by a perfectly diffusing plane surface, varies as the cosine of the angle between that direction and the normal to the surface. The illuminated surface appears equally bright from any angle, however, because the apparent size of the surface, as seen by an observer, will also increase or decrease by a corresponding amount as the viewing angle changes.
For a perfectly diffuse surface that has a reflectance value of one, the luminance of the surface can be expressed in terms of the illuminance falling on that surface as follows:
| Lv = | Ev |
| π |
where:
Lv is the luminance in candela per square metre (cd/m 2)
Ev is the illuminance in lux (lx)
The luminance Lv of a point light source in a given direction is given by the following formula:
| Lv = | d 2Φv |
| dΣdΩcosΣ θΣ |
where:
Lv is the luminance in candelas per square metre (cd/m 2)
d 2Φv is the luminous flux in lumens (lm) leaving area dΣ in any direction contained within the solid angle dΦΣ
dΣ is the infinitesimal area in square metres (m 2) of the point light source
dΩΣ is the infinitesimal solid angle in steradians (sr) in the specified direction
θΣ is the angle between the normal to dΣ and the specified direction
If the medium through which the light travels from the point light source is "lossless" the luminance in a given direction will remain the same, regardless of distance.
We are not going to delve too deeply into the mathematical concepts behind this formula. Suffice it to say that, in order to accurately calculate the luminance of a surface due to the light falling on that surface from a particular light source would require a considerable amount of computation. For many applications, this is simply not practical, but there are various techniques available for obtaining a reasonably accurate approximation.
For those of you who are interested in the maths, the relationship between the luminance of a reflecting surface and the illuminace received by that surface is given by the following formula:
| ∫ | Lv dΩΣ cosθΣ = Mv = Ev R | |
| ΩΣ |
Where the integral covers the emissions for all directions of emission ΩΣ and:
Mv is the luminous exitance of the surface
Ev is the illuminance received by the surface
R is the reflectance of the surface
For a perfectly diffuse (i.e. Lambertian) reflecting surface, the luminance is isotropic, and the relationship between luminance and illuminance becomes much simpler:
Lv = Ev R/π
Light measurement devices fall into two very broad categories - those that measure light radiometrically, which provide an objective measure of light based on light of all wavelengths and typically produce results in terms of Watts (power) or Joules (energy), and those that measure light photometrically, which provide a subjective measure of light based on the average sensitivity of the human eye to wavelengths in the visible spectrum.
It is the latter kind of light measurement device, which produces results in terms of photometric units, that interests us here. We should therefore be careful when discussing photometry, and when investigating the applications of photometers, to distinguish between those instruments designed purely for measuring photometric quantities, and those designed for the measurement of a much wider range of (radiometric) quantities.
Purely photometric instruments are typically used to measure quantities like luminous flux (analogous to radiometric power), luminous intensity (the luminous flux per unit solid angle, i.e. in a given direction), and illuminance (the luminous flux falling on a given surface area). The respective units for these quantities are the lumen (lm), the candela (cd) and the lux (lx).
Before modern photometric instruments were developed, photometric measurement was largely carried out through a process of comparing a subject light source of unknown intensity with one or more light sources for which the intensity was already known. The process relied heavily on human powers of observation, and the ability of the human eye to distinguish between light sources of different intensities.
Perhaps the earliest example of a "photometer", believed to have been invented during the early part of the nineteenth century, consists of a piece of paper with a grease spot in the centre which is mounted in a moveable frame, forming a crude screen. The grease has the effect of making the paper translucent (almost transparent).
The screen is placed between two light sources, A and B. Let’s assume that the intensity of light source A is known, and that we wish to find the intensity of light source B. Light source A (a candle or electric light bulb) is lit. When you look at the screen from the same side as light source A, the grease spot appears darker than the surrounding paper, because more light passes through the paper at that point instead of being reflected back in your direction.
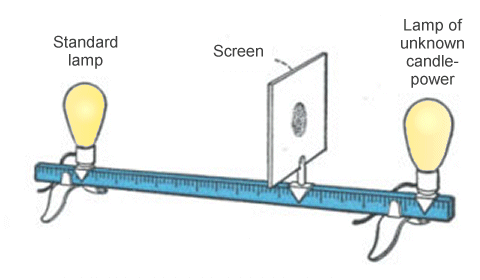
A simple grease-spot photometer
If you look at the screen from the other direction, the grease spot will appear brighter than the area surrounding it because more light is coming through the screen towards you at that point.
Light source B should now be lit, and you should resume your original position. You should now find when looking at the screen that the spot is less dark than it was the first time you observed it, because some light is now coming through it in the opposite direction from light source B (in fact, depending on the intensity of light source B, it may even appear brighter than the surrounding paper).
The idea is to move the screen backwards and forwards between the light sources until the grease spot is no longer visible from either side (or at least until it looks the same from both sides). You should find that there is just one point between the two light sources where this occurs, because each side of the screen will be illuminated to the same degree.
We already know that the illuminance falling on a point due to a light source is inversely proportional to the distance between the light source and the point being illuminated. From this, we can deduce that the ratio of the luminous intensities of our two light sources will be equal to the ratio of the squares of the distances between each light source and the screen, when the screen is at the point where both sides of the screen receive the same illumination.
We can express this relationship algebraically. Let's call the distance between light source A and the screen d1 , and the distance between light source B and the screen d2 . Then we have:
| IvA | = | d1 2 |
| IvB | d2 2 |
where:
IvA is the luminous intensity of light source A
and
IvB is the luminous intensity of light source B
Re-arranging the equation, we get:
| IvB = | IvA × d2 2 |
| d1 2 |
The kind of apparatus we have described above is relatively easy to set up - in a school or college laboratory, for example - is relatively cost effective, and provides reasonably accurate results if care is taken with the observations and measurements.
To consistently measure photometric quantities with a high degree of accuracy, we would obviously require a far more sophisticated photometric measuring device. Most modern photometers detect the light coming from a light source using electronic components such as photoresistors, photodiodes or photomultipliers.
The specification of a particular photometer will depend on the application area for which it is intended. One application with which you are probably familiar is photography, in which the levels of light present in a scene will determine how long the camera's sensor (or film, in the case of an old-fashioned non-digital camera) should be exposed to light coming thgrough the camera's aperture.
At one time, photographers used a light meter (sometimes called an exposure meter), which was a totally separate piece of equipment from the camera itself, to measure ambient light levels before taking a picture. Today, most cameras have a built-in light meter that, by default, controls shutter speeds automatically, although professional photographers or serious amateur photographers often still use a separate device to check light levels.
One important application of photometry is the evaluation of lighting conditions in the workplace. Lighting levels should be sufficient to ensure that employees can perform their work comfortably and efficiently, which means that there must be an appropriate level of light falling on surfaces where operatives are working. Excessive contrast, glare, and flickering light sources in the field of vision can also cause problems.
The measurement of lighting levels in the workplace is mainly concerned with making sure that there is adequate and - as far as possible - uniform illumination over the work area to meet the requirements of a particular type of work activity. The metric of interest is thus illuminance (i.e. the amount of light falling on a unit area of the work surface). The instrument used for making the requisite measurements is a lux meter.
The total luminous flux generated by a light source (a lamp or lightbulb, for example) is often measured using a device called an integrating sphere photometer. As the name suggests, these devices take the form of a hollow sphere, mounted in rigid frame, and typically made of fibreglass or aluminium. The sphere can vary in size from a few centimetres to several metres in diameter, and the inside of the sphere is uniformly coated with a white, highly reflective and highly diffuse material.
The source of light to be measured can either be placed inside the sphere or mounted flush with an opening in the surface of the sphere called an entrance port so that all of the light from the light source enters the sphere. Light from the light source is reflected internally by the sphere’s reflective coating. Because of the diffuse nature of the coating, the light reflected at each point on the inner surface of the sphere is reflected equally in all directions.
The reflected light from the light source is measured by a detector, mounted within another opening in the surface of the sphere called an exit port. A baffle, coated in the same material as the inside of the sphere, prevents any light from the light source falling directly on the detector. Only indirect light that has been reflected many times, i.e. "integrated", will reach the detector. The output of the light source being tested is typically compared with that of one or more standard light sources with known output values, against which the integrating sphere has been calibrated for luminous flux.
There are a number of other kinds of instrument for measuring light measurement instrument. A goniophotometer, for example, is frequently used to measure the light output from solid-state lighting (SSL) devices that use LEDs of various kinds, because these light sources tend to be directional. A goniophotometer is essentially used to measure the light emitted from a light source at different angles.
Goniophotometers have been more widely used in recent years because of strict regulations relating to the spatial distribution of light in automotive applications. A goniophotometer can also be used to determine the total luminous flux of a light source by taking measurements from a comprehensive range of angles. The process is relatively time consuming by comparison with using an integrating sphere, but provides significantly more accurate results.