| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Volume is the amount of space occupied by an object or substance. It is one of the derived quantities defined by the International system of Units. The unit of volume is the cubic metre (m3). This is what is called a coherent derived unit of quantity because it is expressed purely in terms of one of the base units defined by the International system of Units, namely length. Whereas length has the metre (m) as its unit, volume has the cubic metre. In fact, for a number of basic three-dimensional shapes, we can find the volume of an object quite easily simply by measuring its dimensions, in whatever unit of length is appropriate (e.g. metres, centimetres or millimetres) and then applying the correct formula to those measurements to determine its volume. The simplest possible example is probably the cube, which by definition has the same length in all three dimensions. If we had a cube-shaped object for which each side measured two metres (2 m) for example, the volume would be 2 × 2 × 2 cubic metres, which would give us eight cubic metres (8 m3). The formulae for a number of common three-dimensional shapes are given in the following table.
| Shape | Formula | Dimension(s) measured | |||
|---|---|---|---|---|---|
| Cube | a 3 | a = length of each edge | |||
| Rectangular prism (cuboid) |
l × w × h | l = length, w = width, h = height | |||
| Prism | B × h | B = area of base, h = height | |||
| Pyramid |
|
B = area of base, h = height | |||
| Regular tetrahedron |
|
a = length of each edge | |||
| Cylinder | π r 2 h | r = base radius, h = height | |||
| Cone |
|
r = base radius, h = height | |||
| Sphere |
|
r = radius of sphere | Ellipsoid |
|
a, b and c = semi-axes of ellipsoid |
Of course, not all of the things for which we want to find a volume are regular three-dimensional shapes, and not all of them are solids. We might want to find the volume of a gas or a liquid. We might also want to find the volume of a quantity of some solid material that is normally found in powdered or granular form (for example flour, sugar, salt, sand or cement powder). Even if the object of interest is a rigid or semi-rigid item, it may well have a highly irregular shape. In such a case, it is usually not possible (or at least very difficult) to attempt to find the volume of such an object by taking its measurements. Fortunately, there are a number of techniques that can be used to find the volume of things that are not regularly-shaped solids.
Probably the next easiest thing to measure the volume of (after regular solids) is a liquid. The liquid can be poured into a graduated measuring vessel of some kind, and its volume can then be seen by looking at the graduations on the side of the measuring vessel. Although the SI unit of volume is the cubic metre (m3), the volume of a liquid is usually expressed in terms of litres (or submultiples of a litre). A litre has the same volume as a cubic decimeter (a decimeter is one tenth of a metre). A cubic metre of a liquid is thus equivalent to one thousand litres (1000 L). To put this another way, one litre is the equivalent of one thousandth of a cubic metre (1 L = 0.001 m3). For very small amounts of a liquid we would express the volume in either centilitres (a centiliter is one hundredth of a litre) or millilitres (a millilitre is one thousandth of a litre).
The type of measuring vessel used to measure the volume of a liquid will depend on the amount of liquid we need to measure and the degree of accuracy with which the volume must be measured. If we are measuring the amount of water or olive oil (for example) required for a food recipe, a simple household measuring jug is more than adequate. If, on the other hand, we worked in the medical profession and wanted to administer a specific amount of medication a patient either orally or intravenously, the accuracy of our measurement becomes much more important. We would probably want to use a more specialised device to ensure we were giving the patient the correct amount of medication. Accuracy is also important when we want to carry out experiments involving chemicals in solution in a laboratory. Getting the amounts wrong can significantly affect the outcome of the experiment.

A household measuring jug is used to measure the volume of liquids in the kitchen
You may notice from the illustration above that the measuring jug can be used to measure volumes of liquid of up to one pint or half a litre (a half-litre is slightly less than a pint). Although there are a number of non-metric units of measurement still in widespread use for measuring the volume of a liquid (including the pint, of course), we are only interested here in the litre and its sub-multiples. Something else to notice is that the measuring jug is graduated on the half-litre side at intervals of fifty millilitres (50 ml). This is accurate enough for measuring out a volume of liquid to be used in cooking, but it is not really good enough for laboratory use. For more accurate measurements, we can use a measuring vessel like the graduated cylinder illustrated below. This usually takes the form of a tall, relatively narrow, straight-sided vessel made of glass or plastic.

A typical graduated cylinder
The illustration below shows the top section of the graduated cylinder, somewhat enlarged. If you look at the top row of numbers on the image, you will see the expression "500:5". This indicates that the cylinder is graduated up to a maximum level of five hundred millilitres, and that each minor graduation represents an increment in volume of five millilitres. The second row of numbers contains the expression "± 5 in 20° C". This means that the volume measurement is accurate to within (plus or minus) five millilitres at a temperature of twenty degrees centigrade. This raises an important point, which is that the volume of a liquid can vary considerably with temperature. Most measuring vessels are calibrated at, or close to, a temperature of twenty degrees centigrade. This temperature is what is generally considered to be room temperature.

The top section of the graduated cylinder, enlarged
We can find the volume of an amount of liquid simply by pouring it into a graduated cylinder (sometimes called a volumetric cylinder, since its primary purpose is for measuring the volume of a liquid), and reading off the volume using the numbered graduations on the side of the cylinder. There are however a few points to note about using this method. First of all, whenever you transfer an amount of liquid from one container to another, a small amount remains in the original container. The amount of liquid that "sticks" to the original container often depends on the nature of the fluid itself. For example, if we pour water from one glass container into another (being careful not to spill any, of course), the amount of water remaining in the original container is usually negligible. The same is not true of a more viscous fluid such as treacle. Even a relatively free-flowing liquid such as vegetable oil can leave a significant residue in the original container. This is just something to keep in mind for future reference.
Once we have transferred the liquid into the graduated cylinder, reading off the volume also requires a certain amount of care. At the risk of stating the obvious, any vessel used to measure the volume of a liquid should always be placed on a flat, level surface. Even then, as the illustration below shows, the surface of a liquid confined in a relatively narrow vessel will not be completely level. Due to the surface tension of the liquid (a discussion of which belongs elsewhere), the surface of the liquid has a tendency to curve upwards wherever it meets the sides of the container. This curvature (called the meniscus) can be clearly seen with the naked eye. The volume should be read at the lowest level of the surface of the liquid, making sure that the eye is level with the surface of the liquid. Note that If you want to transfer an exact amount of liquid into a measuring vessel, which is often the case, minor adjustments to the level can be made using an eye-dropper (the thing used to administer eye drops).
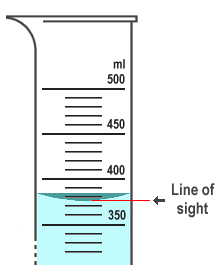
The reading should be taken using the lowest level of the water
Finding the volume of irregularly-shaped solid objects using measurements is often impractical. We can find the exact volume of an irregularly-shaped solid object relatively easily however, using a method known as fluid displacement. Bear in mind that because the method involves immersing the object in a liquid (usually water), you should make sure that the object in question can be safely immersed in the liquid without either damaging the object or creating a hazardous situation. Metallic elements such as lithium and potassium and many common chemical compounds can react quite violently when brought into contact with water. Bear in mind also that adding small amounts of soluble substances such as salt to the water will not cause any significant increase in its volume. As the salt dissolves in the water, its molecules simply occupy the spaces in between the water molecules. Of course, if you continue to add salt there will eventually be too much for it all to dissolve and the volume will increase.
There are several possible ways to use fluid displacement to find the volume of an irregularly shaped object, providing the object is small enough to fit into a volumetric vessel of some kind (remember that the word volumetric indicates that the vessel's primary purpose is the measurement of volume). The first method we will describe involves using a graduated cylinder or similar volumetric vessel. Fill the cylinder about two-thirds full with water. We will assume that the object we want to find the volume of is a small, irregularly shaped object of some kind, and that it is denser than water and will thus sink. You could use a small irregularly-shaped stone or pebble to test the method.

Use a small stone or pebble to test the method
The first thing to do is to read the volume of the water in the measuring vessel and record the value. Once you have done this, you need to get the object into the water so that it is totally submerged. One way of doing this would be to tilt the vessel slightly and allow the object to slide down the side into the water. Dropping the object into a glass container is not a good idea, especially if it relatively heavy. First of all, this can cause some of the water to splash out of the container, which will affect the accuracy of your result. Second, there is the possibility (however slim) that the object will break through the bottom of the container. This will make a mess (water everywhere), create a hazard (due to the broken glass), and incur unnecessary cost (the cost of replacing the vessel). One alternative would be to tie a cotton thread around the object and lower it gently into the water until the object is submerged. The thread itself has negligible volume and will not significantly affect the result.
Once the object is fully immersed in the water, a second reading is taken of the water level in the graduated cylinder or beaker (or whatever). Subtracting the first reading from the second will give you the volume, in millilitres, of the object. To express the volume in cubic metres (or submultiples thereof), simply apply the appropriate conversion factor. One millilitre has the same volume as one cubic centimetre, which is one millionth of a cubic metre (0.000 001 m3, or 10-6 m3). Incidentally, if the object you are trying to find the volume of is less dense than water it will float, rather than sinking to the bottom of the container. If this is the case, you will need to find a method of submerging the object. You might be able to push the object under the water with a thin piece of wire, or alternatively a weight could be tied to the object, to make sure that it sinks. You just need to take the first reading with the weight immersed in the water, so that the difference between the first and second readings gives you just the volume of the object itself.
A second method of finding the volume of an object that relies on fluid displacement involves the use of an overflow vessel and a measuring cylinder, as illustrated below. With this method, the overflow vessel is filled with water until the water starts to overflow and run out of the vessel through the outlet tube on the side of the vessel (the overflow vessel should of course be positioned so that the outlet tube is over a sink, or some suitable receptacle that can catch the excess water). Once the water has stopped overflowing, the measuring cylinder is placed under the outlet tube, and the object is lowered slowly into the overflow vessel. The idea is that a volume of water equivalent to the volume of the object will be displaced, and will flow out of the overflow vessel into the measuring cylinder. The object's volume can then be read directly, by reading the volume of the water in the measuring cylinder.
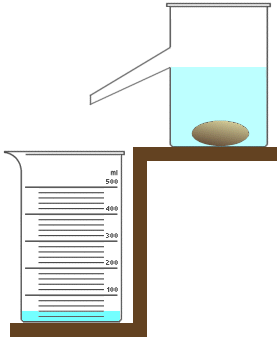
An overflow vessel can be used together with a measuring cylinder