| Author: | |
| Website: | |
| Page title: | |
| URL: | |
| Published: | |
| Last revised: | |
| Accessed: |
Virtually all programming languages can be used to write programs that allow users to work with numeric values and carry out mathematical operations with varying degrees of complexity, and JavaScript is no exception. There are two important built-in objects in the JavaScript language that facilitate working with numbers - the Math object and the Number object. We will be looking at the properties and methods offered by both of these objects - and how to use them - in this article.
As we have stated elsewhere, JavaScript is considered to be a loosely typed language, which amongst other things means that the type of a variable does not have to be declared. The variable's type is assumed by JavaScript based on the value assigned to it when it is initialised. The variable's type can also change. For example, we can assign a numeric value to a variable initially, and later assign a non-numeric value to the same variable without JavaScript complaining.
This makes JavaScript far more flexible than a strongly-typed programming language, but that flexibility comes at a cost. Because there are virtually no restrictions when it comes to data typing, we need to exercise a lot more care when writing code because there are none of the checks and balances associated with a strongly-typed language like Java. Converting a variable from a string to a number, or vice versa, is often done implicitly, depending on the kind of operation being carried out and the nature of the variable, or variables, involved.
A function that expects a numeric value as one of its arguments will not cause a script to crash if it instead receives a string value or a Boolean value. On the other hand, it may not behave quite as we expected either, and we can demonstrate this with an example. The following code generates a web page with a form that allows the user to enter two numeric variables:
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>JavaScript Demo 65</title>
<style>
caption { font-weight: bold; }
form {
width: max-content;
margin: 1em auto;
padding: 0.25em;
border: 1px solid black;
}
#output { border: 1px solid black; }
table { padding: 0.5em; }
td {
padding: 0.5em;
margin: 0.5em;
}
</style>
</head>
<body>
<form id="frm">
<table>
<caption>Calculate Values</caption>
<tr>
<td><label>Variable 1: <input type="number" name="var1"></label></td>
</tr>
<tr>
<td><label>Variable 2: <input type="number" name="var2"></label></td>
</tr>
<tr>
<td><button name="add">Add variables</button></td>
</tr>
<tr>
<td><button name="mul">Multiply variables</button></td>
</tr>
<tr>
<td id="output"><label>Result: <output name="out"></output></label></td>
</tr>
</table>
</form>
<script>
const frm = document.getElementById("frm");
frm.add.addEventListener("click", calc);
frm.mul.addEventListener("click", calc);
function calc() {
event.preventDefault();
let a = frm.var1.value;
let b = frm.var2.value;
if ( event.target === frm.add ) {
result = a + b;
}
else if ( event.target === frm.mul ) {
result = a * b;
}
frm.out.innerHTML = result;
}
</script>
</body>
</html>
Copy and paste this code into a new file in your HTML editor, save the file as javascript-demo-65.html, and open the file in a web browser. You should see something like the illustration below. Try entering different values - both numeric and non-numeric - into the form's input fields, and click the "Add variables" and "Multiply variables" buttons to see what happens. Depending on the values you input and which button you click, you should see something like the illustration below.
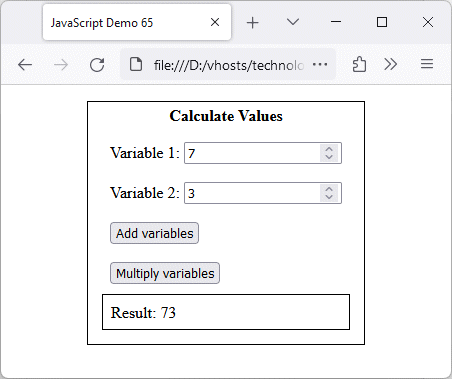
The add() function concatenates the input values
In the above example, we entered values of 7 and 3 and clicked on the "Add variables" button. You may have seen in the HTML code that both of the <input> elements have their type attribute set to number, so we would expect the add() function to add the two numbers together to produce a result of 10. Instead, we see the result 73. Instead of adding the numbers together, the function has concatenated them! The reason for this is that all <input> elements return a string, even if their type attribute is set to number.
One of the slightly confusing features of JavaScript is that the plus sign (+) is both the mathematical operator that represents addition and the string concatenation operator. As far as JavaScript is concerned, the add() function has received two string values as input and has therefore concatenated them, resulting in a string value of "73" being displayed in the <output> field rather than the sum of the two numeric variables we have entered.
However, if we enter the same two values and click on the "Multiply variables" button, the result is exactly what we intended - an output value of 21. That is because JavaScript sees the multiplication operator and assumes that the input values are numeric, so it multiplies them together.
Note that, depending on which browser you are using, the input fields may or may not accept a non-numeric string value as input. The end result of attempting to do so will be the same, however. Even if the browser does allow you to enter non-numeric values, they will effectively be interpreted as having a value of zero.
We can of course force JavaScript to convert a string representing a numeric value into a numeric value, and there is (as is usually the case with JavaScript) more than one way to achieve this. We could, for example replace this line of code:
result = a + b;
with this:
result = parseInt(a) + parseInt(b);
This code is perfectly OK if we are entering only integer (whole number) values, but the result will be inexact for floating-point values, because the parseInt() function truncates any floating-point number it encounters by removing the fractional part, leaving only the integer part. A better option is to use either the parseFloat() function or the unary addition operator (+). Either of the following statements would provide a far more precise result:
result = +a + +b;
result = parseFloat(a) + parseFloat(b);
We still need to exercise caution, however. If we enter fractional values value into the input boxes, both of the above statements can return a result that is not quite right. Let's look at an example. Suppose we enter the values 7.911 and 23.7 in the "Variable 1" and "Variable 2" input fields. You can probably do the addition in your head, which would give you a result of 31.611. However, using either of the statements above produces a result of 31.610999999999997!
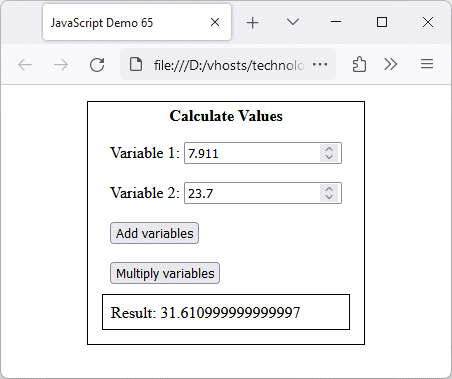
Floating-point errors can occur in JavaScript
In many applications, this discrepancy is not problematic. The degree of error is miniscule, and we can use the JavaScript Number object's toFixed() method (more about that in due course) to tidy things up and display the correct result. The problem occurs because computers store decimal numbers internally as binary numbers. This works perfectly well for integer values, but many decimal fractions have no exact binary equivalent, so floating-point numbers are stored as close approximations.
In most programming languages this is not such an obvious problem because those languages offer numerical data types with varying degrees of precision. Both Java and C++ have the int (integer), float (single-precision floating point), and double (double-precision floating point). JavaScript has only one numeric data type - all numeric values are stored as 64-bit double precision floating point values.
For most applications, it's relatively easy to write code that handles mathematical calculations correctly, and produces the results we are expecting, using the methods provided by the Math and Number objects. For each mathematical operation to be carried out, we should clearly define the nature of the input and output values involved, and devise suitable test cases to ensure that our code is behaving in accordance with the application's requirements.
As we have already mentioned, all numeric values in JavaScript are stored as 64-bit double precision floating point numbers. The numbers are stored in their binary representation in accordance with the IEEE 754 standard double-precision binary floating-point format, which is officially referred to as binary64. A binary64 number is structured as shown in the illustration below.
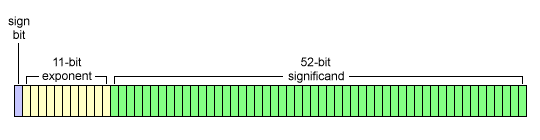
The structure of a binary64 number
The sign bit, as the name suggests, represents the sign of the number (positive = 0, negative = 1), even if the number is zero. The 11-bit exponent field has an unsigned integer value in biased form, in the range 0 to 2047. The term biased form means that the number is offset from the number actually being represented by another number called the exponent bias, which in this case is a zero offset of 1023.
The exponent is stored in this way because it must be able to represent both positive and negative values, but the usual method of representing signed numbers (two's complement) would make binary comparisons more difficult. Putting it another way, an unsigned exponent expressed as a regular binary number is simply easier to work with than an exponent that is represented using two's complement.
The actual exponent is derived by subtracting the exponent bias from the (unsigned) biased exponent. Thus, zero is represented by the biased exponent 1023. The exponent values that can be represented range from -1022 to +1023. The values -1023 (all bits set to 0) and +1024 (all bits set to 1) are reserved for special numbers.
The 53-bit significand consists of the 52 bits in the significand field (you might also see this called the fraction, coefficient, argument, mantissa, or characteristic) prefixed by an implicit binary 1 (sometimes called the "hidden" bit), followed by a binary point (the binary equivalent of the decimal point).
The 11-bit width of the exponent in a binary64 floating point number allows numeric values (positive or negative) with a magnitude of between 1.7976931348623157e-308 and 1.7976931348623157e+308 to be represented, with a precision of around 17 decimal digits. The formula for extracting the value of a number N stored in binary64 format is:
N = (-1) sign × (1.b51 b50 b49 . . . b0 )2 × 2 e-1023
The first part of this formula looks rather strange, but it simply produces a value of +1 or -1 by raising -1 to the power of the sign bit, which is either 1 (for a negative value) or 0 (for a positive value):
-1 1 = -1
-1 0 = +1
The absolute value derived by multiplying the significand by 2 e-1023 is then multiplied by this value to give a positive or negative result.
The largest value that can be stored in the 53-bit significand (including the "hidden" bit) is:
1.1111111111111111111111111111111111111111111111111111
So how do we convert a decimal (base-10) number to binary64 format? Determining the sign bit is of course a trivial matter, since it will be either 0 or 1, depending on whether the number is positive or negative. Determining the binary values of the exponent and the significand is a little trickier. Let's start by looking at how to convert a decimal integer to binary64. We'll use the number 36510 as an example.
Converting 36510 to binary, we get 101101101. In order to get this value into the required format for the significand, we need to shift the binary point to the left until we have only a single binary one to the left of the binary point. In this case, that means shifting the binary point eight places to the left, resulting in a binary value of 1.01101101. So far so good, but how do we find the value of the exponent?
Actually, it's fairly straightforward. Because we had to shift the binary representation of 36510 eight places to the left to get the significand in the required format, we have to multiply the significand by 2 8 in order to restore it to its original value. Remember, however, that the exponent is expressed in biased form with a zero offset of 1023. Our exponent will therefore be the binary equivalent of 8 + 1023, so the calculation is as follows:
810 + 102310 = 103110 = 100000001112
The binary64 representation of 36510 will therefore comprise the elements shown below. Note that the presence of the leading binary 1 (the so-called "hidden" bit) and the binary point that follows it are implied. Only the bits that follow the binary point in the significand are stored in its binary64 representation.
| Sign bit: | 0 |
| Exponent: | 10000000111 |
| Significand: | 0110110100000000000000000000000000000000000000000000 |
If the number we want to convert is a fraction, or has a fractional component, we can follow the same procedure. As an example, let's suppose we want to convert the decimal value 57.89 to its binary64 representation. We start by converting 57.8910 to its binary equivalent:
| 111001.11100011110101110000101000111101011100001010010 |
The six binary digits to the left of the binary point represent the value 5710 exactly. The binary digits to the right of the binary point represent the fractional part of the number (0.8910 ) to 47 significant binary digits, which is the closest approximation possible.
In fact, there is no exact binary representation for the decimal fraction 0.8910 , even if we had an infinite number of binary digits available after the binary point. The bit-pattern that extends from the 3rd position after the binary point to the 22nd position after the binary point - 10001111010111000010 - will simply repeat itself forever.
Note that, due to rounding, the final two digits in the significand are 10 rather than 01. The general rule when rounding binary fractions to n places after the binary point is that, if the digit that would otherwise follow the nth-placed digit is a binary 1 (which is the case here), then the number should be rounded up.
In order to convert the binary representation of 57.8910 into a valid binary64 significand, we need to move the binary point five places to the left, so our exponent will be the binary equivalent of 5 + 1023. We now have enough information to be able to write the binary64 representation of 57.89:
| Sign bit: | 0 |
| Exponent: | 10000000100 |
| Significand: | 1100111100011110101110000101000111101011100001010010 |
You will rarely if ever need to convert a decimal number into its binary64 representation. If for some reason you do have to do this, there are online resources available for that purpose, such as the Online Binary-Decimal Converter utility provided by François Grondin. It is however important to understand the way in which JavaScript and other languages store double-precision floating point numbers, if only to gain an awareness of the limits imposed by the binary64 format on the precision with which numeric values can be stored.
Because of the way numbers are stored in JavaScript, the largest integer value that can be represented safely in JavaScript is 2 53-1, or 9,007,199,254,740,991, because we only have 53 bits available for storing the significand (including the "hidden" bit, which normally has a value of 1). This number is represented in binary64 format as follows:
| Sign bit: | 0 |
| Exponent: | 10000110011 |
| Significand: | 1111111111111111111111111111111111111111111111111111 |
We could of course represent larger integer values by increasing the size of the exponent, but since we can't increase the number of bits available for the significand, this represents a loss of precision. For example, for numbers in the range 2 53 - 2 54, only even numbers will be accurately represented, as demonstrated below. There is thus no reliable way to represent any integer value greater than 2 53-1 in the binary64 format.
console.log(9007199254740992); // 9007199254740992
console.log(9007199254740993); // 9007199254740992
console.log(9007199254740994); // 9007199254740994
console.log(9007199254740995); // 9007199254740996
console.log(9007199254740996); // 9007199254740996
console.log(9007199254740997); // 9007199254740996
console.log(9007199254740998); // 9007199254740998
console.log(9007199254740999); // 9007199254741000
console.log(9007199254741000); // 9007199254741000
console.log(9007199254741001); // 9007199254741000
console.log(9007199254741002); // 9007199254741002
The largest positive and negative safe integer values can be accessed using two special properties of the JavaScript Number object - the constants: Number.MAX_SAFE_INTEGER and Number.MIN_SAFE_INTEGER, which represent the values 9,007,199,254,740,991 and -9,007,199,254,740,991 respectively.
Does this mean we can't express or use integer values with an absolute value greater than 2 53-1? Actually, the answer is no. JavaScript provides the built-in BigInt object for this purpose. A bigint primitive can represent integer values too large to be represented by the number primitive, and can be created by appending "n" to the end of an integer literal. For example:
let x = 9007199254740991n;
let y = x + 10n;
console.log(x); // 9007199254740991n
console.log(y); // 9007199254741001n
console.log(typeof(x)); // bigint
console.log(typeof(y)); // bigint
We can also create a BigInt value using the BigInt() constructor (without the new keyword):
let x = BigInt(9007199254740991);
let y = x * x;
console.log(x); // 9007199254740991n
console.log(y); // 81129638414606663681390495662081n
console.log(typeof(x)); // bigint
console.log(typeof(y)); // bigint
We don't use the new keyword with the BigInt() constructor because it returns a bigint primitive rather than an object, and is therefore not considered to be a constructor method as such. You should also exercise caution when using the BigInt() method to coerce an arbitrarily large integer value to a BigInt value, because loss of precision can occur. For example:
console.log(BigInt(12345678901234567890)); // 12345678901234567168n
You can avoid this problem by putting the numeric argument inside quotes, like this:
console.log(BigInt("12345678901234567890")); // 12345678901234567890n
From the above, we can see that we can represent integer values that are greater in magnitude than MAX_SAFE_INTEGER and MIN_SAFE_INTEGER. We can also use these values together with JavaScript's arithmetic operators to carry out calculations. There are a couple of things to note, however. The first is that all values used in a calculation must be of type bigint. As we saw above, the following code works:
let x = 9007199254740991n;
let y = x + 10n;
console.log(y); // 9007199254741001n
The following code does not work as expected:
let x = 9007199254740991n;
let y = x + 10;
console.log(y); // Uncaught TypeError: can't convert BigInt to number
The only difference between these two code snippets is that we have omitted the "n" from the end of the numeric literal "10" in the second line, so JavaScript throws a type error. The second thing to note is that BigInt values cannot be used with the built-in methods provided by the Math object. You should also be aware that, even though it is possible to coerce Number values to BigInt values and vice versa, the precision of a BigInt value may be lost when it is coerced to a Number value.
Most of JavaScript's operators support the bigint type to a greater or lesser extent although, with one or two exceptions, all of the operands involved must be BigInt values. Another caveat is that calculations involving BigInt values will always return BigInt values. This means that, whereas operations involving addition, subtraction or multiplication will always produce a correct result, the result of dividing one BigInt value by another will only produce a correct result if the divisor is a factor of the dividend:
let x = 9n;
console.log(x/3n); // 3n (result is correct)
console.log(x/2n); // 4n (result rounded down to nearest BigInt value)
One advantage of the bigint type is that for some arithmetic operations involving integer values it can yield results of greater precision than the same operations carried out with integers of the number type. For example:
let num = 25 ** 30;
let big = 25n ** 30n;
console.log(num); // 8.673617379884035e+41
console.log(big); // 867361737988403547205962240695953369140625n
The size of a BigInt value is only limited by the amount of computer memory available for storing it, so even really huge integer values can be represented with no loss of precision. The largest Number value, on the other hand, is represented by the constant Number.MAX_VALUE, which represents a value of 1.7976931348623157e+308 (approximately 2 1024), which has a precision of 17 significant digits.
As we have already stated, an exponent of 1024 is reserved for special use, so the largest number we can actually store in binary64 format has an exponent of 1023, with all of the bits in the significand being set to 1. If the binary point after the first digit in the significand is shifted 52 places to the right, we will have the integer 9,007,199,254,740,991 (the value represented by MAX_SAFE_INTEGER).
Shifting the binary point a further 971 places to the right will give us the value 9,007,199,254,740,991 × 2 971 = 1.7976931348623157e+308 to 17 significant digits - the number represented by Number.MAX_VALUE. As we saw above, the fact that we only have 53 binary digits available for the significand in binary64 numbers (including the hidden bit) means that, as we increase the size of the exponent, there is an increasing loss of precision.
If we decrease the value of the significand by changing the last binary digit from a 1 to a 0, for example, the resulting binary64 number converts to a decimal value of 1.7976931348623155e+308 to 17 significant digits. At first glance this does not seem to be so very different from the value given for Number.MAX_VALUE. In fact, the difference between the two values is 2e+292 - a staggeringly large number!
We can store some very large values in binary64 format, but we will lose more and more precision as the size of the numbers increases. If we really need to carry out calculations involving such large numbers, we should consider using BigInt. As a general rule, however, BigInt should only be used if our code is required to deal with values greater than 2 53. Another thing to avoid, as we have mentioned previously, is coercion between Bigint and Number values, which can result in loss of precision.
One final thing to note is that the numeric argument passed to the BigInt() constructor method does not have to be a base-10 (decimal) value. It can also be a binary, octal or hexadecimal number, although care must be taken to append the correct prefix to the value passed as an argument. Note also that, regardless of the argument's number base, the BigInt value is stored as a base-10 number. The following code illustrates how this works:
const myBin = BigInt(0b10011010010);
const myOct = BigInt(0o2322);
const myHex = BigInt(0x4d2);
console.log(myBin); // 1234n
console.log(myOct); // 1234n
console.log(myHex); // 1234n
We can also create BigInt values by appending the "n" suffix to binary, octal or hexadecimal numbers, as the following code demonstrates:
const myBin = 0b10011010010n;
const myOct = 0o2322n;
const myHex = 0x4d2n;
console.log(myBin); // 1234n
console.log(myOct); // 1234n
console.log(myHex); // 1234n
Although BigInt values can be of an arbitrary size, it is possible to set a limit on the number of bits to be used using the static BigInt.asIntN() and BigInt.asUintN() methods. The first of these, BigInt.asIntN(), takes two arguments, both of which are numeric values. The value received as the first argument specifies the maximum number of bits that can be used to store the value received as the second argument.
In the following example, the checkInput() function accepts a numeric value as input, converts it to a BigInt value, and checks to see whether that value can be stored as a 16-bit integer. If so, it returns the BigInt value. Otherwise, it returns a message indicating that the input is out of range.
const maxBits = 16;
function checkInput(input) {
let value = BigInt(input);
if( value === BigInt.asIntN(maxBits, value)) {
return value;
}
else {
return "Input is out of range.";
}
}
console.log(checkInput(32767)); // 32767n
console.log(checkInput(32768)); // Input is out of range.
console.log(checkInput(-32768)); // -32768n
console.log(checkInput(-32769)); // Input is out of range.
The static BigInt.asUintN() method works in a similar fashion, except that it works with unsigned inters. Whereas a 16-bit signed integer can represent values between -32768 and +32767, a 16-bit unsigned integer can represent values in the range 0 to 65535. Note however that the input to BigInt.asUintN() must also be an unsigned integer value. The following code snippet shows what happens if a negative integer value is passed to this method:
console.log(BigInt.asUintN(16, -65n)); // 65471n
As you can see, the numeric value of the BigInt value returned is the maximum value of a 16-bit unsigned integer (65535), plus 1, minus the absolute value of the input value, i.e. (65535 + 1) - 65 = 65471. If we want to use the BigInt.asUintN() method to work with negative values, we have to convert those values to their unsigned equivalents.
The code below contains the function absBigInt(), which takes a positive or negative integer value as input and either returns its absolute value as a 16-bit unsigned BigInt value or (if it requires more than 16 bits) displays a message stating that it is not in range.
const maxBits = 16;
function absBigInt(input) {
let value = BigInt(input);
if (value < 0) {
value = value * -1n;
}
let absVal = BigInt.asUintN(maxBits, value);
if (absVal === value) {
return absVal;
}
else {
return "Input is out of range.";
}
}
console.log(absBigInt(+65535)); // 65535n
console.log(absBigInt(+65536)); // Input is out of range.
console.log(absBigInt(-65535)); // 65535n
console.log(absBigInt(-65536)); // Input is out of range.
If we are creating an application that works with BigInt values we will almost certainly need to display those values on screen at some point. BigInt provides two methods that allow us to convert a BigInt value into a string value - Bigint.prototype.toString() and Bigint.prototype.toLocaleString(). Both of these methods are instance methods, which means that, unlike BigInt.asIntN() and BigInt.asUintN(), they can be called directly on a bigint primitive. For example:
let myBigInt = 1024n;
console.log(myBigInt); // 1024n
console.log(typeof myBigInt); // bigint
let myString = myBigInt.toString()
console.log(myString); // 1024
console.log(typeof myString); // string
The Bigint.prototype.toString() method takes an optional radix argument that specifies the number base used to present the numeric value it is called on. The values accepted are integer values in the range 2-36, although there will seldom if ever be a requirement to pass radix values other than 2 (binary), 8 (octal) or 16 (hexadecimal). The following code demonstrates how this works:
const myNum = 234n;
console.log(myNum.toString(2)); // 11101010
console.log(myNum.toString(8)); // 352
console.log(myNum.toString(16)); // ea
When the radix argument is not specified, it defaults to a value of 10. Note that, although the values displayed are correct binary, octal or hexadecimal representations of the value toString() is called on, the resulting string does not include the binary (0b), octal (0o), or hexadecimal (0x) prefix that is normally used to signify the base of the number represented.
If any of these strings were to be passed to a function expecting a numeric argument, such as BigInt(), they would be treated as base-10 values or (in the case of the hexadecimal value, which contain non-numeric characters) cause a syntax error. We can circumvent this problem by appending the appropriate prefix to the string created by the toString() method. For example:
const myNum = 234n;
const myBin = "0b" + myNum.toString(2);
const myOct = "0o" + myNum.toString(8);
const myHex = "0x" + myNum.toString(16);
console.log(myBin); // 0b11101010
console.log(myOct); // 0o352
console.log(myHex); // 0xea
console.log(BigInt(myBin)); // 234n
console.log(BigInt(myOct)); // 234n
console.log(BigInt(myHex)); // 234n
The BigInt.prototype.toLocaleString() method also converts a numeric value to a string, but is used when we want to present the string in a language-specific format. This method accepts two arguments, both of which are optional (although see below). The first of these is the locales argument, which consists of the ISO 639-1 language code and the ISO 3166-1 country code, separated by a hyphen. For example:
const myNum = 123456789n;
console.log(myNum.toLocaleString("de-DE")); // 123.456.789
console.log(myNum.toLocaleString("en-GB")); // 123,456,789
console.log(myNum.toLocaleString("en-IN")); // 12,34,56,789
The second argument is the options argument, which can be used to more precisely specify the output format. For example:
const myNum = 123456789n;
console.log(myNum.toLocaleString("de-DE",
{ style: "currency", currency: "EUR" })); // 123.456.789,00 €
The last BigInt method we will briefly look at here is the BigInt.prototype.valueOf() method, which is used to return the wrapped primitive value of a BigInt object. The following code demonstrates how it works:
const myObj = Object(123n);
const myBigInt = myObj.valueOf();
console.log(myObj); // BigInt { }
console.log(typeof myObj); // object
console.log(myBigInt); // 123n
console.log(typeof myBigInt); // bigint
As we have previously stated, all variables of type number are stored in binary64 format. This means that the largest positive integer value that can be represented safely in JavaScript is 2 53 - 1, and the largest negative integer value that can be represented safely is -2 53 + 1. Arbitrarily large integer values can be represented as BigInt values, although care must be taken when coercing integer values of type bigint to type number and vice versa (as a general rule we should avoid coercion between these types if possible).
When it comes to floating point numbers, we can work with much larger values. Positive and negative values with magnitudes of between 2 -1022 (2.2250738585072014e-308) and 2 1024 (1.7976931348623157e+308) can be represented, with a precision of around 17 decimal digits. What this means in real terms is that we can represent both very large numbers and very small numbers which, if written in their full decimal form rather than in scientific notation, could have over 300 decimal digits. Precision, on the other hand, is limited to 16 or 17 decimal digits because we only have 53 binary digits in which to store the number's significand.
For the kind of floating-point values we generally have to deal with when writing applications, this degree of precision is usually perfectly adequate. Keep in mind, however, that although some numbers with fractional components such as 0.625, 0.5, 0.25 or 0.125 can be represented exactly in binary form, the vast majority cannot. If a fraction can be raised to some power of two to arrive at a whole number, it can be represented exactly as a binary fraction, otherwise its binary representation will be an approximation.
The fractional component of a binary floating-point number consists of some number of binary digits following the binary point, each representing 2 -n where n represents the position the binary digit occupies in relation to the binary point. Consider the binary number 1010.101. The digits to the left of the binary point represent an integer value - in this case 10102 = 1010 . The value to the right of the binary point (.101) can be evaluated as follows:
Fractional component: 2 -1 + 0 + 2 -3 = 0.5 + 0 + 0.125 = 0.625
The decimal value 10.625 can thus be represented exactly as a binary number, and has seven significant (binary) digits. Unfortunately, as we have indicated, most decimal fractions have no exact binary equivalent, so a binary representation of the fractional part of a decimal floating-point value is almost always an approximation rather than an exact representation. This would be the case even if we had an unlimited number of binary digits available after the binary point, which of course we don't.
To illustrate the point, let's consider the decimal fraction 0.1 (i.e. one tenth, or 1/10). To convert a fractional value to its binary representation, we multiply it repeatedly by two. Each time we do so, we note down the integral part, and repeat the procedure for the fractional part of the result. We keep repeating this process until the fractional part becomes zero, or until we can see a repeating pattern:
2 × 0.1 = 0.2 (0)
2 × 0.2 = 0.4 (0)
2 × 0.4 = 0.8 (0)
2 × 0.8 = 1.6 (1)
2 × 0.6 = 1.2 (1)
2 x 0.2 = 0.4 (0)
2 x 0.4 = 0.8 (0)
2 x 0.8 = 1.6 (1)
2 x 0.6 = 1.2 (1)
By now it should be fairly obvious that, as we continue the process, the sequence of results (0.4, 0.8, 1.6, 1.2) will repeat itself forever, which means that following the first binary digit in the sequence, the bit-pattern 0011 will also repeat itself forever. The binary representation of the decimal fraction 0.1 (0.0001100110011 . . . . ) will therefore always be an approximation. How good that approximation is depends on the number of bits we use to represent the binary fraction.
That brings us to another point. The total number of bits available for the significand of a binary64 double-precision value is 53, including the so-called "hidden" bit. These bits represent both the integer part and the fractional part of a floating-point number. The magnitude of that number depends on the value stored in the 11-bit exponent field, which can range from -1022 to +1023.
In order to derive the value stored in the binary64 format, the significand is multiplied by 2 n, where n represents the exponent. Essentially, the exponent tells us how far to the left (in the case of a negative exponent) or to the right (for a positive exponent) we need to move the binary point in the significand in order to obtain the stored value as a binary number.
For numbers with a large integer component, more bits will be required to represent that part of the number, leaving fewer bits available to represent the fractional part, and resulting in a loss of precision. There is therefore a trade-off between the magnitude of a floating-point number and the precision to which its fractional component (assuming one exists) is represented. In truth, we are rarely if ever interested in in a fractional component when dealing with very large numbers.
Given that the exponent and the significand in a binary64 number are limited to 11 and 53 binary digits respectively, the number of different floating-point values that can be stored in this format, although very large, is finite. The limited precision of binary64 numbers means that there are gaps between consecutive values, the magnitude of which for a given range of numbers can be determined according to the size of the exponent.
To demonstrate how this works, let's consider a greatly scaled-down and simplified floating-point system in which the significand consists of five binary digits (including a "hidden" bit), and exponents can range from -2 to +2. For the purposes of this exercise, we will only concern ourselves with positive numbers, so the sign bit will always be zero. The exponent is stored in three bits with an exponent bias of 2, and can have valid values of 0002 , 0012 , 0102 , 0112 and 1002 . This system, which we'll call "Binary8", can represent eighty different numeric values, from 0.2510 to 7.7510 (0.012 to 11.112 ).
| Binary8 Format | Base-2 Calculation | Base-2 Value | Base-10 Value |
|---|---|---|---|
| 00000000 | 1.0000 x 2-2 | 0.010000 | 0.250000 |
| 00000001 | 1.0001 x 2-2 | 0.010001 | 0.265625 |
| 00000010 | 1.0010 x 2-2 | 0.010010 | 0.281250 |
| 00000011 | 1.0011 x 2-2 | 0.010011 | 0.296875 |
| 00000100 | 1.0100 x 2-2 | 0.010100 | 0.312500 |
| 00000101 | 1.0101 x 2-2 | 0.010101 | 0.328125 |
| 00000110 | 1.0110 x 2-2 | 0.010110 | 0.343750 |
| 00000111 | 1.0111 x 2-2 | 0.010111 | 0.359375 |
| 00001000 | 1.1000 x 2-2 | 0.011000 | 0.375000 |
| 00001001 | 1.1001 x 2-2 | 0.011001 | 0.390625 |
| 00001010 | 1.1010 x 2-2 | 0.011010 | 0.406250 |
| 00001011 | 1.1011 x 2-2 | 0.011011 | 0.421875 |
| 00001100 | 1.1100 x 2-2 | 0.011100 | 0.437500 |
| 00001101 | 1.1101 x 2-2 | 0.011101 | 0.453125 |
| 00001110 | 1.1110 x 2-2 | 0.011110 | 0.468750 |
| 00001111 | 1.1111 x 2-2 | 0.011111 | 0.484375 |
| 00010000 | 1.0000 x 2-1 | 0.100000 | 0.500000 |
| 00010001 | 1.0001 x 2-1 | 0.100010 | 0.531250 |
| 00010010 | 1.0010 x 2-1 | 0.100100 | 0.562500 |
| 00010011 | 1.0011 x 2-1 | 0.100110 | 0.593750 |
| 00010100 | 1.0100 x 2-1 | 0.101000 | 0.625000 |
| 00010101 | 1.0101 x 2-1 | 0.101010 | 0.656250 |
| 00010110 | 1.0110 x 2-1 | 0.101100 | 0.687500 |
| 00000111 | 1.0111 x 2-1 | 0.101110 | 0.718750 |
| 00011000 | 1.1000 x 2-1 | 0.110000 | 0.750000 |
| 00011001 | 1.1001 x 2-1 | 0.110010 | 0.781250 |
| 00011010 | 1.1010 x 2-1 | 0.110100 | 0.812500 |
| 00011011 | 1.1011 x 2-1 | 0.110110 | 0.843750 |
| 00011100 | 1.1100 x 2-1 | 0.111000 | 0.875000 |
| 00011101 | 1.1101 x 2-1 | 0.111010 | 0.906250 |
| 00011110 | 1.1110 x 2-1 | 0.111100 | 0.937500 |
| 00011111 | 1.1111 x 2-1 | 0.111110 | 0.968750 |
| 00100000 | 1.0000 x 20 | 1.000000 | 1.000000 |
| 00100001 | 1.0001 x 20 | 1.000100 | 1.062500 |
| 00100010 | 1.0010 x 20 | 1.001000 | 1.125000 |
| 00100011 | 1.0011 x 20 | 1.001100 | 1.187500 |
| 00100100 | 1.0100 x 20 | 1.010000 | 1.250000 |
| 00100101 | 1.0101 x 20 | 1.010100 | 1.312500 |
| 00100110 | 1.0110 x 20 | 1.011000 | 1.375000 |
| 00100111 | 1.0111 x 20 | 1.011100 | 1.437500 |
| 00101000 | 1.1000 x 20 | 1.100000 | 1.500000 |
| 00101001 | 1.1001 x 20 | 1.100100 | 1.562500 |
| 00101010 | 1.1010 x 20 | 1.101000 | 1.625000 |
| 00101011 | 1.1011 x 20 | 1.101100 | 1.687500 |
| 00101100 | 1.1100 x 20 | 1.110000 | 1.750000 |
| 00101101 | 1.1101 x 20 | 1.110100 | 1.812500 |
| 00101110 | 1.1110 x 20 | 1.111000 | 1.875000 |
| 00101111 | 1.1111 x 20 | 1.111100 | 1.937500 |
| 00110000 | 1.0000 x 21 | 10.000000 | 2.000000 |
| 00110001 | 1.0001 x 21 | 10.001000 | 2.125000 |
| 00110010 | 1.0010 x 21 | 10.010000 | 2.250000 |
| 00110011 | 1.0011 x 21 | 10.011000 | 2.375000 |
| 00110100 | 1.0100 x 21 | 10.100000 | 2.500000 |
| 00110101 | 1.0101 x 21 | 10.101000 | 2.625000 |
| 00110110 | 1.0110 x 21 | 10.110000 | 2.750000 |
| 00110111 | 1.0111 x 21 | 10.111000 | 2.875000 |
| 00111000 | 1.1000 x 21 | 11.000000 | 3.000000 |
| 00111001 | 1.1001 x 21 | 11.001000 | 3.125000 |
| 00111010 | 1.1010 x 21 | 11.010000 | 3.250000 |
| 00111011 | 1.1011 x 21 | 11.011000 | 3.375000 |
| 00111100 | 1.1100 x 21 | 11.100000 | 3.500000 |
| 00111101 | 1.1101 x 21 | 11.101000 | 3.625000 |
| 00111110 | 1.1110 x 21 | 11.110000 | 3.750000 |
| 00111111 | 1.1111 x 21 | 11.111000 | 3.875000 |
| 01000000 | 1.0000 x 22 | 100.000000 | 4.000000 |
| 01000001 | 1.0001 x 22 | 100.010000 | 4.250000 |
| 01000010 | 1.0010 x 22 | 100.100000 | 4.500000 |
| 01000011 | 1.0011 x 22 | 100.110000 | 4.750000 |
| 01000100 | 1.0100 x 22 | 101.000000 | 5.000000 |
| 01000101 | 1.0101 x 22 | 101.010000 | 5.250000 |
| 01000110 | 1.0110 x 22 | 101.100000 | 5.500000 |
| 01000111 | 1.0111 x 22 | 101.110000 | 5.750000 |
| 01001000 | 1.1000 x 22 | 110.000000 | 6.000000 |
| 01001001 | 1.1001 x 22 | 110.010000 | 6.250000 |
| 01001010 | 1.1010 x 22 | 110.100000 | 6.500000 |
| 01001011 | 1.1011 x 22 | 110.110000 | 6.750000 |
| 01001100 | 1.1100 x 22 | 111.000000 | 7.000000 |
| 01001101 | 1.1101 x 22 | 111.010000 | 7.250000 |
| 01001110 | 1.1110 x 22 | 111.100000 | 7.500000 |
| 01001111 | 1.1111 x 22 | 111.110000 | 7.750000 |
The range of floating-point numbers we are able to represent with our "Binary8" system could of course be extended by increasing the number of bits in the exponent and changing the bias accordingly. We could also improve precision by increasing the number of bits in the significand. The intention here, however, is to demonstrate the limitations imposed when using a fixed-width binary format to represent base-10 floating-point values.
Looking at the table above, we can see that, like any fixed-width number format, the range of values that can be represented is discontinuous - there are significant gaps between successive values. Note also that the size of the gap between two consecutive values is the same for a given exponent. The interval between consecutive values in the range 1 × 2 -2 and 1 × 2 -1 is has a constant value of 0.0000012 (0.01562510 ). For values in the range 1 × 2 -1 and 1 × 2 0, the size of the interval is 0.000012 (0.0312510 ) - double the size of the interval in the preceding range.
We can see that, for any range of values between 1 × 2 n and 1 × 2 n+1, increasing the value of n by one will double the size of the interval between consecutive values within that range. Any fixed-width binary representation of floating-point values - including the binary64 double-precision floating-point format used by JavaScript and other programming languages - will suffer a similar loss of precision as the magnitude of the numbers it represents grows.
As the size of the interval between consecutive floating-point values increases, the number of intervals between successive integer values declines. In our "Binary8" scheme, there are sixteen intervals between the integer values 1 and 2. Between 2 and 3, and between 3 and 4, there are eight intervals each. Between 4 and 5 there are six intervals, and between 5 and 6 there are only four intervals.
If we extrapolate this pattern, it becomes clear that at some point we will only be able to accurately represent integer values. At some further point, we will not even be able to represent consecutive integer values. This is exactly what happens in the binary64 representation of floating-point values. With a 53-bit significand (including the "hidden" bit), all floating-point values between 2 52 and 2 53 are consecutive integer values. We are unable to represent consecutive integers greater than 2 53, which is why the Number.MAX_SAFE_INTEGER constant is set to 2 53-1.
We said earlier that positive and negative values with magnitudes of between 2-1022 (2.2250738585072014e-308) and 21024 (1.7976931348623157e+308) can be represented in binary64 format. It should therefore come as no surprise that one of the properties of the Number object, which we'll be looking at shortly, is the constant Number.MAX_VALUE, which represents the largest value we can represent in JavaScript:
console.log(Number.MAX_VALUE); // 1.7976931348623157e+308
There is however another property of the Number object called Number.MIN_VALUE, which gives us the smallest positive value we can represent in JavaScript:
console.log(Number.MIN_VALUE); // 5e-324
This value is considerably smaller than 2.2250738585072014e-308, which is the smallest normalised non-zero binary64 value. What do we mean by "normalised"? When we talk about normal binary64 numbers, we assume two things.
First, we assume that the exponent field will have a minimum value of 000000000012 , which equates to -102210 when we take into account the exponent bias (102310 ). The second assumption is that the "hidden" bit will always be 1, which for normalised binary64 numbers is indeed the case. Here is the binary64 representation of 2.2250738585072014e-308:
| Sign bit: | 0 |
| Exponent: | 00000000001 |
| Significand: | 0000000000000000000000000000000000000000000000000000 |
Remember, the "hidden" bit is always set to 1 for normalised binary64 numbers. Therefore, in order to convert this binary64 representation to a base-10 number, the calculation is:
1 × 2-1022 = 2.2250738585072014e-308
Small as this value is, there is a significant gap between it and zero. If we can't represent smaller values in JavaScript, what will happen if, for example, we divide this value by two? Let's try it:
const smallFloat = -2.2250738585072014e-308;
console.log(smallFloat/2); // -1.1125369292536007e-308
Which is the correct result. Sometimes, a calculation results in a value too small to be represented as a normal binary64 number, creating a condition known as arithmetic underflow (or floating-point underflow or just underflow). The interval between zero and the smallest normal floating-point value is called the underflow gap, and is much larger than the gaps between consecutive normal floating-point values just outside the underflow gap by several orders of magnitude.
Prior to 1984, if the result of a floating-point calculation turned out to be in the underflow gap, it would typically be converted to zero, either at the hardware level or by the system software responsible for handling an underflow condition - an action known as "flushing to zero".
The 1984 version of the IEEE 754 standard (see above) introduced subnormal numbers (sometimes called denormal numbers). These subnormal numbers, which include zero, occupy the underflow gap. The interval between consecutive subnormal numbers is the same as the interval between consecutive normalised binary64 values that lie immediately above the underflow gap - a value known as machine epsilon. If the result of a floating-point calculation lies within the underflow gap, its value is converted to the nearest subnormal value (which could, of course, be zero).
According to the above definition, we should be able to obtain a value for machine epsilon by subtracting the smallest positive normal binary64 number (2.2250738585072014E-308) from the next smallest positive binary64 number (2.2250738585072019E-308), which results in a value of 5e-324, which you may recall is the value of Number.MIN_VALUE. The interval between any two adjacent subnormal numbers, as well as the interval between zero and Number.MIN_VALUE, is equal to machine epsilon.
Subnormal numbers are too small to be represented as normal floating-point numbers. They are still represented as 64-bit values, but in a format somewhat different to that of normal floating-point numbers. In a subnormal (or denormalised) number, all of the exponent bits are set to zero. If at least one bit in the significand is non-zero, the value is interpreted as a subnormal number with an exponent of -1022, otherwise it will be interpreted as zero. The "hidden" bit before the binary point now has a value of 0.
The value of a subnormal number Ns is given by the following formula:
Ns = (-1)sign × 2-1022 × 0.f
where f is the (fractional) value stored in the significand. Here is the binary64 representation of the smallest positive non-zero subnormal value:
| Sign bit: | 0 |
| Exponent: | 00000000000 |
| Significand: | 0000000000000000000000000000000000000000000000000001 |
Inserting these values into the formula for a subnormal number, we get:
Ns = (-1)0 × 2-1022 × 2-52
Ns = 1 × 2-1074
Ns = 4.9406564584124654417656879286822e-324
This is not quite the same value as Number.MIN_VALUE (5e-324), and we have been unable to find any literature that explains why there is this discrepancy. It may have been a matter of notational convenience, since both of these base-10 values are represented by exactly the same binary64 subnormal number, and could be used interchangeably in calculations involving subnormal values. According to MDN's documentation:
"Number.MIN_VALUE is the smallest positive number . . . that can be represented within float precision - in other words, the number closest to 0 . . . In practice, its precise value in mainstream engines . . . is 2-1074, or 5E-324."
JavaScript's built-in Number object provides a wrapper for primitive values of type number. If the Number() method is used with the new keyword, it acts as a constructor method and creates another object of type Number. If used without the new keyword, it creates a primitive of type number. In practice, we rarely need to create additional Number objects, because the properties and methods of the Number object are available to number primitives. Consider the following code:
const numPr1 = 100;
const numPr2 = Number(100);
const numObj = new Number(100);
console.log(typeof numPr1); // number
console.log(typeof numPr2); // number
console.log(typeof numObj); // object
console.log(numObj === numPr2); // false
console.log(numObj == numPr2); // true
console.log(numPr2 === numPr1); // true
console.log(numObj.valueOf()); // 100
The first thing to note here is that Number() used as a function creates a primitive of type number. The following statements both create primitive values of type number:
const numPr1 = 100;
const numPr2 = Number(100);
Using the new keyword with Number() creates a Number object, although if we pass an argument of 100, the value of that object will be 100. That's why the following two lines of code return different results:
console.log(numObj === numPr2); // false
console.log(numObj == numPr2); // true
The == operator (equality) and the === operator (strict equality) differ in that the == operator carries out type conversion before it makes a comparison, and subsequently only compares the values of its operands. The === operator, on the other hand, compares both the values and the data types of its operands in order to establish equality. As a rule, you should avoid creating objects of type Number.
The following table lists the Number object's properties and briefly describes the purpose of each.
| Property | Description |
|---|---|
| Number.EPSILON |
A static property that represents the difference between 1 and the smallest floating-point value of type number greater than 1 (2.220446049250313e-16). |
| Number.MAX_SAFE_INTEGER |
A static property that returns the maximum safe integer value that can be taken by a variable of type number (253-1 or 9,007,199,254,740,991). |
| Number.MAX_VALUE |
A static property that returns the maximum positive value that can be taken by a variable of type number (1.7976931348623157e+308). |
| Number.MIN_SAFE_INTEGER |
A static property that returns the minimum safe integer value that can be taken by a variable of type number (-253+1 or -9,007,199,254,740,991). |
| Number.MIN_VALUE |
A static property that returns the smallest positive value that can be taken by a variable of type number (5e-324). |
| Number.NaN |
A static property that represents Not-A-Number - equivalent to the global NaN property. |
| Number.NEGATIVE_INFINITY |
A static property that represents any negative value that has a magnitude greater than that of Number.MAX_VALUE. |
| Number.POSITIVE_INFINITY |
A static property that represents any positive value that has a magnitude greater than that of Number.MAX_VALUE. |
The Number object has a number of methods that are available to any primitive of type number. The following table lists the Number object's methods and briefly describes the purpose of each. Note that some of the methods defined for the Number object have global equivalents that have either the same, or similar, functionality.
| Method | Description |
|---|---|
| Number.isFinite() |
A static method that returns true if the argument passed to it evaluates to a finite number, and false if it evaluates to positive infinity, negative infinity, or NaN. For example:
console.log(Number.isFinite(2e+308)); // false Similar to the global isFinite() method except that it does not convert the argument passed to it to a number. Only arguments of type number that are finite will return true. Non-number values always return false. |
| Number.isInteger() |
A static method that returns true if the argument passed to it is an integer value, otherwise returns false. For example:
console.log(Number.isInteger(255)); // true |
| Number.isNan() |
A static method that returns true if the argument passed to it is the number value NaN, otherwise returns false. For example:
console.log(Number.isNaN(NaN)); // true Similar to the global isNaN() method except that it does not convert the argument passed to it to a number. Only arguments of type number that are also NaN will return true. Non-number values always return false. |
| Number.isSafeInteger() |
A static method that returns true if the argument passed to it is an integer value in the range -253 +1 to 253 -1, otherwise returns false. For example:
console.log(Number.isSafeInteger(55)); // true |
| Number.parseFloat() |
A static method that parses the string value supplied to it as an argument and returns a floating-point number or, if the string value cannot be coerced to a floating-point number, returns NaN. For example:
console.log(Number.parseFloat(" 123.45 ")); // 123.45
Leading and trailing spaces are ignored. |
| Number.parseInt() |
A static method that parses the string value supplied to it as its first argument and returns an integer value using the radix passed to it as the (optional) second argument, or to base-10 if no radix is specified or is set to 0 . For example:
console.log(Number.parseInt(" 123 ")); // 123
If specified, the radix argument must be either 0 or an integer value in the range 2 - 36, otherwise NaN is returned. If the radix argument is undefined or 0, base-10 is assumed. |
| toExponential() |
An instance method that returns a string representing the number on which it is called in exponential notation, with one digit before the decimal point. For example:
const myFloat = 123.4567;
The method accepts an optional fractionDigits argument that specifies the number of digits to display after the decimal point. If used, the fractionDigits argument must be an integer value in the range 0 - 100. |
| toFixed() |
An instance method that returns a string representing the number on which is called using fixed-point notation, whereby a fixed number of digits are used to represent the fractional part of the number. For example:
const myFloat = 123.4567;
The method accepts an optional digits argument that specifies how many digits to display after the decimal point. If used, the digits argument must be an integer value in the range 0 - 100. If not specified, the digits argument defaults to 0. |
| toLocaleString() |
An instance method that returns a string representing the number on which it is called using a language-specific format. For example:
const myNum = 123456789;
The method accepts two arguments, both of which are optional. The first of these is the locales argument, which if used typically consists of a two-character language code and a two-character country code separated by a hyphen. |
| toPrecision() |
An instance method that returns a string representing the number on which is called to the specified precision. For example:
const myNum = 123.456;
The optional precision argument specifies the number of significant digits that should be used to represent the number on which the toPrecision() method is called. |
| toString() |
An instance method that returns a string representing the number on which it is called. For example:
const myNum = 123456;
The toString() method takes an optional radix argument that specifies the number base used to present the numeric value it is called on. The values accepted are integer values in the range 2-36. When the radix argument is not specified, or is set to 0, it defaults to a value of 10. |
| valueOf() |
An instance method that returns the primitive value of the number it is called on. For example:
const myNumObj = new Number(0xffff); This method does not take any arguments. It is usually called internally by JavaScript and rarely used explicitly in a web application. |
JavaScript's built-in Math object provides a number of useful mathematical constants and functions. It facilitates the creation of code to handle complex mathematical operations. Unlike most other JavaScript objects, the Math object has no constructor method. You do not need to create an instance of the Math object in order to access its properties and use its methods.
The Math object's static properties include widely-used mathematical constants such as e (Euler's number), which is used for calculations involving exponential growth and decay, both in scientific research and in the finance sector. Other static properties include constants that are ubiquitous in many areas of science, engineering and mathematics, such as the square roots of ½ and 2, frequently used logarithmic values, and of course pi (π), which features heavily in countless geometric and trigonometric formulae used in many branches of mathematics, science and engineering.
The Math object also provides methods that can be used to help us carry out trigonometric calculations, find the sign and absolute value of a number, calculate roots and logarithmic values, find the maximum or minimum value in a set of numeric variables, work with exponential values, truncate or round floating-point numbers, or generate pseudo-random numbers.
The last-mentioned feature - the ability to generate random numbers - will be of particular interest to those engaged in developing gaming applications, because these applications often rely on being able to create random events. An algorithm that produces random numbers is called a random number generator (RNG). Let's see how we might code a web page that can generate six randomly selected lottery numbers in the range 1-49. Here is the code:
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>JavaScript Demo 66</title>
<style>
h1 {text-align: center}
table {
padding: 0.5em;
margin: auto;
}
th, td {
border: 1px solid grey;
padding: 0.5em;
text-align: center;
}
div {
text-align: center;
padding: 0.5em;
}
</style>
</head>
<body>
<h1>Lottery Number Generator</h1>
<table>
<caption>Lottery Numbers</caption>
<thead>
<tr>
<th>1st</th><th>2nd</th><th>3rd</th><th>4th</th><th>5th</th><th>6th</th>
</tr>
</thead>
<tbody>
<tr id="numArray">
<td>-</td><td>-</td><td>-</td><td>-</td><td>-</td><td>-</td>
</tr>
</tbody>
</table>
<div>
<button id="lottoGo">Generate Numbers</button>
</div>
<script>
let btn = document.querySelector("#lottoGo");
btn.addEventListener("click", generateLotteryNumbers);
function getRandomIntInRange(min, max) {
return Math.floor(Math.random() * (max - min + 1) + min);
}
function numCompare(a, b) { return a - b; }
function generateLotteryNumbers() {
const lottery = new Array(6);
const elements = document.getElementById("numArray").children;
let i = 0;
while(i < 6) {
let num = getRandomIntInRange(1,49);
if(!lottery.includes(num)) {
lottery[i] = num;
i++;
}
}
lottery.sort(numCompare);
for(let i=0; i<6; i++) {
elements[i].innerHTML = lottery[i];
}
}
</script>
</body>
</html>
Copy and paste this code into a new file in your HTML editor, save the file as javascript-demo-66.html, open the file in a web browser, and click on the "Generate Numbers" button. You should see something like the illustration below, depending on what random numbers have been generated.
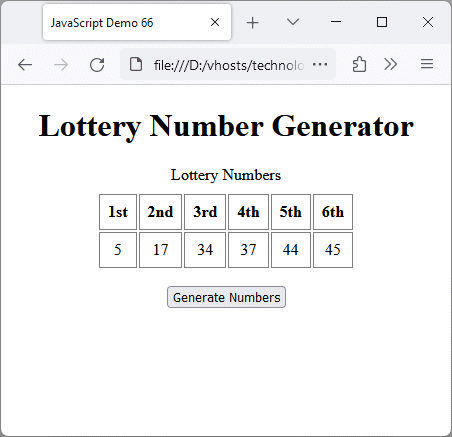
A simple random number generator
If you study the JavaScript code, you will see that we have used two methods belonging to the Math object - Math.random() and Math.floor(). The random numbers are created by the getRandomIntInRange() function. This function finds the difference between the values it receives for min and max, adds 1 to that number, multiplies the result by the output of Math.random() to create a pseudo-random floating-point number, and then adds the value of min to the result. The Math.floor() method is then used to round the result down to the nearest integer value.
The remaining code is fairly self-explanatory. The generateLotteryNumbers() function creates an empty 6-element array to hold the lottery numbers, and calls getRandomIntInRange() repeatedly using a while loop until the array contains 6 unique integer values in the range 1-49. We avoid duplicating any of the numbers in the array by checking each randomly generated number to see if it is already included, in which case it is not added to the array.
Once we have an array containing six different numbers between 1 and 49, the values in the array are sorted by ascending value. Each value is then inserted into a separate table data (<td> . . . </td>) element in a HTML table by assigning it to the element's innerHTML property.
The Math object has a number of static properties that hold mathematical constants. The following table lists the Math object's properties and briefly describes the purpose of each.
| Property | Description |
|---|---|
| Math.E |
A static property that represents Euler's number (e), an irrational number that is widely used in problems relating to exponential growth or decay. It is also the base of the natural logarithm. Its value to 15 decimal places is 2.718281828459045. |
| Math.LN10 |
A static property that represents the natural logarithm of 10 - the power to which Euler's number e must be raised in order to obtain a value of 10. It is an irrational number whose value to 15 decimal places is 2.302585092994046 |
| Math.LN2 |
A static property that represents the natural logarithm of 2 - the power to which Euler's number e must be raised in order to obtain a value of 2. It is an irrational number whose value to 16 decimal places is 0.6931471805599453. |
| Math.LOG10E |
A static property that represents the base-10 logarithm of Euler's number (e) - the power to which 10 must be raised to obtain a value of e. It is an irrational number whose value to 16 decimal places is 0.4342944819032518. |
| Math.LOG2E |
A static property that represents the base-2 logarithm of Euler's number (e) - the power to which 2 must be raised to obtain a value of e. It is an irrational number whose value to 16 decimal places is 1.4426950408889634. |
| Math.PI |
A static property that represents the mathematical constant π (the Greek letter pi), which is the ratio of the circumference of any circle to the diameter of the circle. It is an irrational number whose value to 15 decimal places is 3.141592653589793. |
| Math.SQRT1_2 |
A static property that represents the square root of ½. It is an irrational number whose value to 16 decimal places is 0.7071067811865476. |
| Math.SQRT2 |
A static property that represents the square root of 2. It is an irrational number whose value to 16 decimal places is 1.4142135623730951. |
The JavaScript Math object has a number of methods to facilitate the performance of mathematical operations. The following table lists the Math object's methods and briefly describes the purpose of each.
| Method | Description |
|---|---|
| Math.abs() |
A static method that returns the absolute value of the number passed to it as an argument, regardless of sign. For example:
console.log(Math.abs(1)); // 1 The Math.abs() method attempts to coerce the argument it receives to a value of type number. If a value cannot be coerced to a number, it returns NaN. |
| Math.acos() |
A static method that returns the inverse cosine, in radians, of the number passed to it as an argument. For example:
console.log(Math.acos(2)); // NaN The argument supplied to Math.acos() represents the cosine of an angle, and must be a number in the range -1 to 1. The value returned represents the inverse cosine - an angle in radians, with a value in the range 0 to π. If the argument supplied has a value of less than -1 or greater than 1, Math.acos() returns NaN. |
| Math.acosh() |
A static method that returns the inverse hyperbolic cosine of the number passed to it as an argument. For example:
console.log(Math.acosh(0)); // NaN The argument supplied to Math.acosh() must have a value of 1 or greater. If the argument is less than 1, Math.acosh() returns NaN. |
| Math.asin() |
A static method that returns the inverse sine, in radians, of the number passed to it as an argument. For example:
console.log(Math.asin(-2)); // NaN The argument supplied to Math.asin() represents the sine of an angle, and must be a number in the range -1 to 1. The value represents the inverse sine - an angle in radians with a value in the range -π/2 to π/2. If the argument supplied has a value of less than -1 or greater than 1, Math.asin() returns NaN. |
| Math.asinh() |
A static method that returns the inverse hyperbolic sine of the number passed to it as an argument. For example:
console.log(Math.asinh(-100)); // -5.298342365610589 |
| Math.atan() |
A static method that returns the inverse tangent, in radians, of the number passed to it as an argument. For example:
console.log(Math.atan(-100)); // -1.5607966601082315 |
| Math.atan2() |
A static method that returns the angle, in radians, between the positive x-axis and the ray from the origin (0, 0) to the point x, y whereby the coordinate values x and y are the first and second arguments passed to Math.atan2(). For example:
console.log(Math.atan2(3, 4)); // 0.6435011087932844 |
| Math.atanh() |
A static method that returns the inverse hyperbolic tangent of the number passed to it as an argument. For example:
console.log(Math.atanh(-2)); // NaN The argument supplied to Math.atanh() must be a number in the range -1 to 1. If the argument suplied is 1, Math.atanh() returns Infinity. If the argument is -1, it returns -Infinity, and If it has a value of less than -1 or greater than 1, it returns NaN. |
| Math.cbrt() |
A static method that returns the cube root of the number passed to it as an argument. For example:
console.log(Math.cbrt(-1)); // -1 |
| Math.ceil() |
A static method that rounds up the number passed to it as an argument to the nearest integer, returning the smallest integer greater than or equal to that number. For example:
console.log(Math.ceil(-1)); // -1 |
| Math.clz32() |
A static method that returns the number of leading zero bits in the 32-bit binary representation of the number passed to it as an argument (clz32 stands for Count Leading Zeros 32). For example:
console.log(Math.clz32(-1)); // 0 If the argument passed to Math.clz32() is not a number, it will first be coerced to a number, and then converted to an unsigned 32-bit integer. If the argument is 0 or has a value greater than or equal to 231, the value returned will be 0. If the argument cannot be coerced to a number, the value returned will be 32. |
| Math.cos() |
A static method that returns the cosine, in radians, of the number passed to it as an argument. For example:
console.log(Math.cos(0)); // 1 |
| Math.cosh() |
A static method that returns the hyperbolic cosine of the number passed to it as an argument. For example:
console.log(Math.cosh(-1)); // 1.5430806348152437 |
| Math.exp() |
A static method that returns e raised to the power of the number passed to it as an argument, where e is the base of the natural logarithm. For example:
console.log(Math.exp(-1)); // 0.36787944117144233 Note that if the argument supplied is a value very close to 0, the value returned will be very close to 1 and will suffer from a loss of precision. In such cases, it might be better to use the Math.expm1() method, for which the fractional part of the return value has a much higher precision. |
| Math.expm1() |
A static method that raises e to the power of the number passed to it as an argument, where e is the base of the natural logarithm, and returns the result minus 1. For example:
console.log(Math.expm1(-1)); // -0.6321205588285577 |
| Math.floor() |
A static method that rounds down the number passed to it as an argument to the nearest integer, returning the largest integer less than or equal to that number. For example:
console.log(Math.ceil(-1)); // -1 |
| Math.fround() |
A static method that returns the nearest 32-bit single-precision representation of the number passed to it as an argument. For example:
const val64 = 1.234;
The Math.fround() method is useful if you are working with 32-bit floating-point numbers and need to test for equality with JavaScript variables of type number. |
| Math.hypot() |
A static method that returns the square root of the sum of the the squares of the numbers passed to it as arguments. For example:
console.log(Math.hypot()); // 0 Returns 0 if no arguments are supplied or all of the arguments supplied are ±0. Returns Infinity if any of the arguments supplies are ±Infinity. Returns NaN if one or more of the arguments supplied is not a number and cannot be coerced to a number. |
| Math.imul() |
A static method that returns the product of the two integer values passed to it as arguments. For example:
console.log(Math.imul()); // 0 Returns 0 if no arguments are supplied, or if one of the arguments supplied is 0. If more than two arguments are supplied, all arguments other than the first two are ignored. If either of the arguments supplied have a fractional part, the fractional part is ignored. |
| Math.log() |
A static method that returns the natural logarithm (log to base e) of the number passed to it as an argument. For example:
console.log(Math.log(-1)); // NaN
Returns NaN if no argument is supplied or the argument supplied is less than 0, -Infinity if any the argument is ±0. |
| Math.log10() |
A static method that returns the logarithm to base 10 ) of the number passed to it as an argument. For example:
console.log(Math.log10(-1)); // NaN Returns NaN if no argument is supplied or the argument suppliedis less than 0, -Infinity if any the argument is ±0. |
| Math.log1p() |
A static method that returns the natural logarithm (log to base e) of the number passed to it as an argument + 1. For example:
console.log(Math.log1p(-2)); // NaN Returns NaN if no argument is supplied or the argument supplied is less than -1, and -Infinity if the argument supplied is -1. |
| Math.log2() |
A static method that returns the logarithm to base 2 of the number passed to it as an argument + 1. For example:
console.log(Math.log2()); // NaN Returns NaN if no argument is supplied or the argument supplied is less than 0, and -Infinity if the argument supplied is 0. |
| Math.max() |
A static method that returns the largest of the numbers passed to it as arguments. For example:
console.log(Math.max()); // -Infinity Returns -Infinity if no arguments are supplied, and NaN if any of the arguments suppied is, or evaluates to, NaN. |
| Math.min() |
A static method that returns the smallest of the numbers passed to it as arguments. For example:
console.log(Math.min()); // Infinity Returns Infinity if no arguments are supplied, and NaN if any of the arguments suppied is, or evaluates to, NaN. |
| Math.pow() |
A static method that returns the value of a base raised to a power. This method expects two numbers as arguments. The first argument is the base, and the second argument is the exponent. For example:
console.log(Math.pow()); // NaN The return value will be NaN if:
|
| Math.random() |
A static method that takes no arguments and returns a pseudo-random floating-point value that is greater than or equal to 0 and less than 1. This value can then be used with a given range of values to create a randon value within that range. For example:
Math.random()); // a number between 0 (inclusive) and 1 (exclusive) To generate a random number that falls between two values, we could do something like this:
function getRandomInRange(min, max) { If we want to obtain a random integer that falls between two values, we could do something like this:
function getRandomIntInRange(min, max) { The function getRandomIntInRange() returns an integer value in the specified range, inclusive of both the minimum and maximum integer values passed to it as arguments. |
| Math.round() |
A static method that returns the value of the number passed to it as an argument, rounded to the neares integer. For example:
console.log(Math.round(-10.6)); // -11
A positive number with a fractional part greater than or equal to 0.5 is rounded up to the next largest integer. If the fractional part is less than 0.5, the number is rounded down to the next smallest integer. |
| Math.sign() |
A static method that returns 1 or -1, depending on whether the number passed to it as an argument is a positive or negative value, respectively. For example:
console.log(Math.sign()); // NaN If no argument is supplied, or if the argument supplied cannot be coerced to a number, Math.sign() returns NaN. If the argument supplied is 0 or -0, the return value will be the argument itself (0 or -0). |
| Math.sin() |
A static method that returns the sine, in radians, of the number passed to it as an argument. For example:
console.log(Math.sin(0)); // 0 |
| Math.sinh() |
A static method that returns the hyperbolic sine of the number passed to it as an argument. For example:
console.log(Math.sinh(-1)); // -1.1752011936438014 |
| Math.sqrt() |
A static method that returns the square root of the number passed to it as an argument. For example:
console.log(Math.sqrt(-1)); // NaN |
| Math.tan() |
A static method that returns the tangent, in radians, of the number passed to it as an argument. For example:
console.log(Math.tan(0)); // 0 Note that, because of issues with floating-point precision, it is not possibe to obtain an exact value for π/2 (90°) or π/4 (45°). In trigonometry, the value of tan 90 is generally considered to be infinity (or undefined), and the value of tan 45° is 1. |
| Math.tanh() |
A static method that returns the hyperbolic tangent of the number passed to it as an argument. For example:
console.log(Math.tanh(-1)); // -0.7615941559557649 |
| Math.trunc() |
A static method that returns the integer part of a number passed to it as an argument. For example:
console.log(Math.trunc()); // NaN Any decimal digits to the right of the decimal point are simply discarded, regardless of whether the argument is a positive or negative number. |